При переході
електрона з однієї стаціонарної орбіти на іншу випромінюється або поглинається квант енергії
Співвідношення невизначеностей. Межі використання
Загальне часове рівняння Шредінгера і його аналіз
Частинка в одновимірному потенціальному ящику
Гармонічний квантовий осцилятор
Енергія атома водню і його спектр. Виродження рівнів
Принцип нерозрізненості тотожних частинок. Принцип Паулі
Розподіл електронів за станами
Рентгенівські промені. Суцільний спектр і його межі. Характеристичний спектр. Закон Мозлі
Енергетичні рівні молекул. Молекулярні спектри. Парамагнітний резонанс
Комбінаційне розсіювання світла
Навигация
Частинка в одновимірному потенціальному ящику
Елементи квантової фізики
91515
знаков
1
таблица
26
изображений
1.3.2. Частинка в одновимірному потенціальному ящику
Розглянемо приклад просторово-обмеженого одновимірного руху квантової частинки в глибокому потенціальному ящику з вертикальними стінками, шириною l. Потенціальна енергія електрона зовні і всередині такого ящика має наступні значення:
U(x)=0 при 0<x<l, (1.37)
U(x)=¥ при x£0 й x³ l
Графік залежності потенціальної енергії частинки U(x) від х показаний на рис 1.5.
Частинка в такому ящику може вільно рухатись на ділянці 0<х<l. На кінцях цього інтервалу вона стикається з абсолютно твердими стінками. Непрозорість цих стінок визначається необмеженим ростом потенціальної енергії U(x) в точках х=0 і х=l.
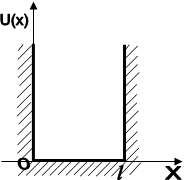
Рис. 1.5
Прикладом руху електрона в потенціальному ящику може бути рух колективізованих електронів усередині металу. Як відомо, в класичній електронній теорії вважали, що поза металом потенціальна енергія електрона дорівнює нулю, а всередині металу - вона від’ємна і чисельно дорівнює роботі виходу електрона з металу. Інакше кажучи, вважали, що рух електронів обмежений потенціальним бар’єром прямокутної форми з плоским дном. В нашому випадку потенціальний ящик значно простішої форми ніж реальний випадок електрона в металі.
Так як частинка не виходить за межі ділянки 0<х<l, то імовірність знайти її за межами цієї ділянки дорівнює нулю. Це означає, що рівняння Шредінгера для стаціонарних станів можна доповнити граничними умовами 
і
Запишемо рівняння Шредінгера для частинки в потенціальному ящику
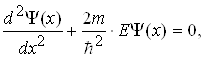(1.38)
де m - маса частинки; 
- стала Дірака; Е - повна енергія частинки; Y(х) - хвильова функція.
Введемо позначення
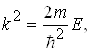(1.39)
де к - хвильове число хвиль де Бройля для електрона, який перебуває усередині потенціального ящика.
Рівняння (1.38) набуде вигляду
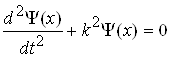(1.40)
Знайдемо розв’язок рівняння (1.40), подібно до аналогічних диференціальних рівнянь гармонічних коливань, в тригонометричній формі
(1.41)
де А,В і С - сталі величині.
З граничних умов одержуємо:
а) Y(0)=0; 0=АcosB.0+CsinB.0
Звідки А=0; В¹0 і С¹0.
б) Y(l)=0; 0=CsinB.l.
звідки при С¹0, Вl=np, або 
де n = 1,2,3........
Хвильова функція з урахуванням граничних умов набуде вигляду:
(1.42)
Константу С у формулі (1.42) знайдемо із умови нормування
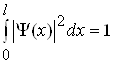(1.43)
або
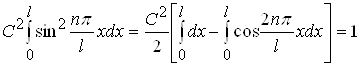. (1.44)
Другий інтеграл у виразі (1.44) при будь-яких значеннях n дорівнює нулю, тому
звідки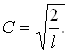 
Хвильова функція, яка описує квантовий рух частинки в потенціальному ящику має вигляд:
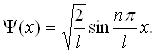(1.45)
При підстановці (1.45) в (1.38) одержуємо тотожність:
.
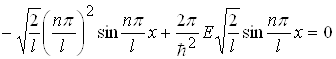Звідки
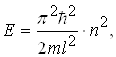(1.46)
тобто енергія Е електрона в потенціальному ящику не може бути довільною. Вона набуває лише дискретних власних значень Е(n). Імовірність виявити в межах потенціального ящика електрон з іншою енергією, ніж (1.46) дорівнює нулю.
Енергетичний спектр і густина імовірності частинки в потенціальному ящику показана на рис. 1.6.
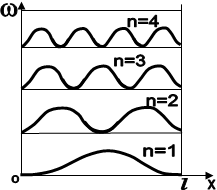
Рис.1.6
Число n в формулі (1.46) визначає вид хвильової функції і енергію частинки в стані з цією хвильовою функцією, називається квантовим числом. Покажемо, що для частинки в потенціальному ящику можливі лише такі енергетичні рівні, на яких викладається ціле число півхвиль де Бройля. При аналізі граничних умов було показано, що kl=np, де 
- хвильове число хвиль де Бройля. З урахуванням останнього маємо:
(1.47)
Співвідношення (1.47) показує, що в потенціальному ящику можливі лише такі стани частинки, при яких на ширині потенціального ящика l вкладається ціле число півхвиль де Бройля (Рис.1.7).
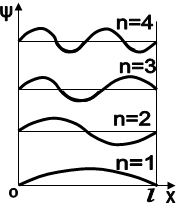
Рис 1.7 Незбуреному стану частинки відповідає енергія
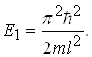(1.48)
Значення цієї енергії Е1>0 свідчить про те, що частинка в потенціальному ящику ніколи не зупиняється і що невизначеність DРх імпульсу частинки не може бути меншою за величину
(1.49)
Однак в потенціальному ящику шириною l положення частинки визначається похибкою, яка співрозмірна з шириною ящика Dх»l
Тому Dх.DРх³p
,
(1.50)
що перебуває у повній відповідності із співвідношенням невизначеностей імпульс - координата.
Покажемо, як залежить ширини енергетичного інтервалу DЕ від розмірів потенціального ящика. У потенціальному ящику з розмірами l=10-9м. Власні значення енергії електрона утворюють послідовність енергетичних рівнів, енергетична відстань між якими дорівнює
DE=En+1-En.
Або
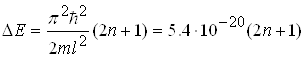Дж.
В електрон-вольтах ця енергія дорівнює
Коли ширина потенціального ящика співрозмірна з розмірами атома, енергетичний інтервал між сусідніми енергетичними рівнями досить значний, а спектр є дискретним.
У випадку, коли потенціальний ящик має мікроскопічні розміри l»10-2м., енергетичний інтервал між сусідніми рівнями дорівнює
Дж=0,34.10-14(2n+1) eB.
Для такого потенціального ящика квантуванням енергії можна знехтувати. Вона нічим не відрізняються від значень енергії, одержаних класичними методами.
Аналогічні результати можна одержати для великих квантових чисел n. У цьому випадку проявляється принцип відносності, встановлений Бором у 1923р.
При великих квантових числах висновки і результати квантової механіки збігаються з відповідними класичними результатами.
Похожие работы
... івнює , а в домішкових напівпровідниках має зміст енергії іонізації донорів чи акцепторів. Отже, питома електропровідність напівпровідників експоненційно збільшується з ростом температури, чим останні принципово відрізняються від металів. Розділ VII. Фізика ядра та елементарних часток. § 7.1. Склад і характеристики ядра Ядро атома, як центральну позитивно заряджену масивну частину атома, ...
... ї й експериментальної фізики, раніше розроблені для вивчення макромолекул небіологічного походження. Неможливо провести границю між молекулярною біофізикою і біофізичною хімією, так само як не можна провести границю між молекулярною фізикою і фізичною хімією. Класифікація областей знання має завжди історичний і не строго визначений характер. Молекулярна фізика і відповідні розділи фізичної хімії ...
... математики. Фізика є теоретичним фундаментом для вивчення професійно-орієнтованих, військово-технічних і військових дисциплін. Тема 1. Кінематика і динаміка матеріальної точки Навчальний потік інженери Час 2 години Місце Навчальна та виховна мета _________________________________________ ____________________________________________________________ Навчальні питання і розподіл часу ...
... на цій же осі. Згідно Френелю, дія такої перешкоди зводиться до того, що екран якби усуває ту частину хвильового фронту, яку він прикриває. На відкритій же частині світлове поле не змінюється. Це наближення геометричної оптики, а тому воно виконується, якщо радіус отвору >> Визначимо розміри і число зон Френеля, що вкладаються в отвір Нехай - діаметр отвору, а та віддалені від його ...
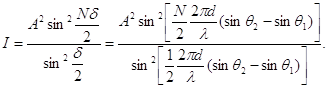
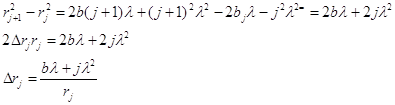
0 комментариев