Навигация
Гармонічний квантовий осцилятор
1.3.3. Гармонічний квантовий осцилятор.
Просторово-обмеженим є також рух квантового осцилятора. З класичної точки зору осцилятором може бути будь-яка матеріальна точка, яка здійснює гармонічні коливання під дією квазіпружної сили.
F=-kx, де k=m![]() (1.51)
(1.51)
Потенціальна енергія класичного осцилятора знаходиться за формулою
![]()
де m - маса частинки; ![]() - циклічна частота осцилятора.
- циклічна частота осцилятора.
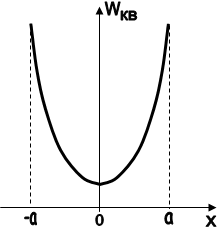 Графічна залежність енергії класичного осцилятора показана на рис.1.8.
Графічна залежність енергії класичного осцилятора показана на рис.1.8.
Рис. 1.8
.
З рисунка видно, що осцилятор може мати практично довільну енергію, навіть рівну нулю. В точках -а і +а кінетична енергія осцилятора дорівнює нулю, а потенціальна енергія досягає свого максимуму. За межі області (-а, +а) класичний осцилятор вийти не може.
Квантовим осцилятором може бути лише елементарна частинка, яка поряд з корпускулярними властивостями проявляє і хвильові властивості. Прикладом квантового осцилятора може бути коливний рух атомів і молекул у вузлах кристалічної гратки. Потенціальна енергія квантового осцилятора має таку ж математичну залежність, що і класичний осцилятор (1.52).
Стаціонарне рівняння Шредінгера для лінійного гармонічного осцилятора має вигляд:
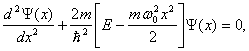 (1.53)
(1.53)
де m - маса квантової частинки; ![]() - циклічна частота; Е - повна енергія частинки.
- циклічна частота; Е - повна енергія частинки.
Знаходження хвильових функцій квантового осцилятора є досить складною математичною задачею. Тому, опускаючи такі розв’язки, наводимо енергетичний спектр квантового осцилятора. Він має вигляд
![]() (1.54)
(1.54)
де n= 0,1,2,3,..... - любе ціле число, починаючи з нуля; ![]() - циклічна частота;
- циклічна частота; ![]() - стала Дірака.
- стала Дірака.
Аналіз рівняння (1.54) показує, що енергетичний спектр квантового осцилятора є дискретним і що власні значення енергії дорівнюють:
![]()
![]()
![]()
В енергетичному спектрі (1.54) проміжки між енергетичними рівнями не залежать від квантового числа n, а є однаковими
![]() (1.55)
(1.55)
Як показано на рис. 1.9, де енергетичний спектр квантового осцилятора суміщається з аналогічним спектром класичного осцилятора, квантовий осцилятор не має значень енергії, рівних нулю.
Найменше значення енергії квантового осцилятора дорівнює
![]() (1.56)
(1.56)
Меншої енергії квантовий осцилятор не може мати навіть при абсолютному нулі температур.
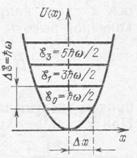
Рис. 1.9
Покажемо наближеним способом, що енергія квантового осцилятора квантується. З рис 1.10 видно, що на відрізку l=2х0 вкладається ціле число півхвиль де Бройля, тобто
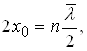 (1.57)
(1.57)
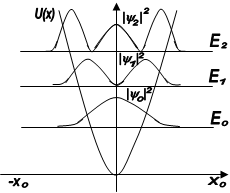
Рис 1.10
де ![]() - середнє значення довжини хвилі де Бройля.
- середнє значення довжини хвилі де Бройля.
Звідки
![]() (1.58)
(1.58)
Середнє значення імпульсу кванта хвилі де Бройля
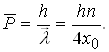 (1.59)
(1.59)
Середня кінетична енергія такого осцилятора
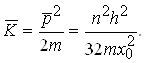 (1.60)
(1.60)
Відомо, що повна енергія Е перевищує середнє значення кінетичної енергії в два рази, тобто
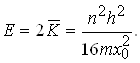 (1.61)
(1.61)
З іншої точки зору повна енергія квантового осцилятора дорівнюватиме максимальній потенціальній енергії
 (1.62)
(1.62)
Перемножимо рівності (1.61) і (1.62)
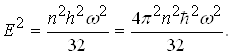 (1.63)
(1.63)
Або
![]() (1.64)
(1.64)
В межах точності наших міркувань ![]() »1, тому
»1, тому
![]() (1.65)
(1.65)
де n =1,2,3,... - цілі числа.
Наближений розрахунок показує, що енергія квантового осцилятора набуває ряду дискретних значень, тобто квантується.
Точне значення енергії квантового осцилятора для не збудженого, нульового рівня можна одержати із рівняння Шредінгера (1.53), якщо згідно рис. (1.10) скористатись функцією Гаусса, яка дорівнює
![]() (1.66)
(1.66)
де а - стала величина, яку слід визначити.
Другу похідну від (1.66) підставимо в (1.53)
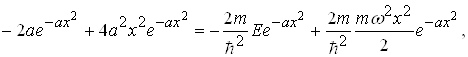
звідки
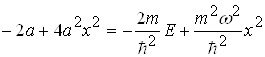 .
(1.67)
.
(1.67)
Тотожність (1.67) має місце при рівності коефіцієнтів при х2 і вільних членів, тобто
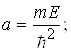
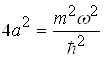 (1.68)
(1.68)
Система рівнянь (1.68) дає значення енергії Е і сталої величини а
![]()
![]() (1.69)
(1.69)
Таким чином функція Гаусса є розв’язком рівняння Шредінгера (1.53) лише за умови, коли ![]() .
.
В цьому випадку
 .
(1.70)
.
(1.70)
Слід відмітити, що так як відстань між суміжними рівнями енергії квантового осцилятора дорівнює ![]() то з урахуванням
то з урахуванням ![]() одержуємо енергетичний спектр квантового осцилятора у вигляді
одержуємо енергетичний спектр квантового осцилятора у вигляді
 (1.71)
(1.71)
де n = 0,1,2,3....
1.3.4.Проходження частинки крізь потенціальний бар’єр. Тунельний ефект.
Класична частинка не може перебувати в тих місцях, де її потенціальна енергія U(x) перевищувала б повну енергію частинки E. Щодо квантової частинки, то вона має таку властивість із-за того, що існує відмінна від нуля імовірність проникнення її крізь потенціальний бар’єр, тобто в область, де U(x) > E
Проведемо оцінку цієї імовірності шляхом розв’язування наступної задачі. Нехай квантова частинка з масою m, рухаючись в напрямі осі х, вдаряється в потенціальний бар’єр кінцевої висоти U0, тобто

причому енергія частинки e менша висоти бар’єра U0, (рис. 1.11).
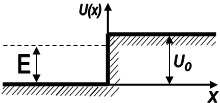
Рис. 1.11
В області потенціального бар’єра рівняння Шредінгера для стаціонарних станів набуде вигляду
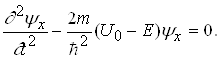 (1.72)
(1.72)
Якщо позначити вираз ![]() через
через ![]() , то рівняння (1.72) перепишеться
, то рівняння (1.72) перепишеться
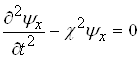 .
(1.73)
.
(1.73)
Розв’язком рівняння (1.34) може бути функція
![]() , (1.74)
, (1.74)
де А і В - деякі константи, і - уявна одиниця.
Експонента з додатним знаком фізичного змісту не має і може бути відкинута, так як не повинно бути зростання імовірності в області потенціального бар’єра. Тому в області потенціального бар’єра (х>0), хвильова функція частинки Yx визначається рівністю
Yx = Be-i![]() x (1.75)
x (1.75)
Коефіцієнт В у виразі (1.75) пов’язаний з інтенсивністю променя частинок, які рухаються в напрямі бар’єра, а тому задається довільно. Як правило х>0 координати частинок розподіляються з густиною імовірності
![]() , (1.76)
, (1.76)
де w(0) дорівнює значенню |Yx|2 при х=0.
Рівняння (1.76) показує, що із збільшенням глибини проникнення в область потенціального бар’єра, густина імовірності w(х) зменшується експоненційно. Це зменшення буде тим швидше, чим більша різниця енергій U0 - E.
Знайдемо глибину проникнення елементарної частинки в область потенціального бар’єра при умові, що m = 9,1 10-31кг (електрон), U0 - E = 10-4 eB, а густина імовірності w(х) на цій відстані зменшується в е разів
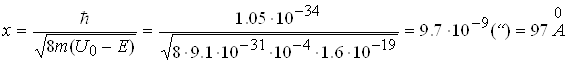 .
.
Ця відстань перевищує на два порядки діаметр атома водню. Глибина проникнення зменшується на порядок, якщо різниця енергій U0 - E зросте до 10-2 еВ.
Здатність квантових частинок проникати в область потенціального бар’єра приводить до тунельного ефекту. Його суть полягає в проникненні частинки із однієї області в іншу область, які поділені потенціальним бар’єром навіть в тих випадках, коли енергія частинки Е менше висоти потенціального бар’єра U0.
Таке проходження частинки виявляється можливим дякуючи існуванню під бар’єром хвильової функції, яка «прокладає» шлях частинки на будь-яку відстань. Тунельний ефект є головною причиною a - розпаду радіоактивних ядер.
2. Фізика атомів і молекул
2.1. Атом водню
2.1.1. Використання рівняння Шредінгера до атома водню.
Хвильова функція. Квантові числа.
2.1.2. Енергія атома водню і його спектр. Виродження рівнів.
Правила відбору.
2.1.3. Механічний і магнітний моменти атома водню.
2.1.1.Використання рівняння Шредінгера до атома водню.
Хвильова функція. Квантові числа.
Теорія Бора будови і властивостей енергетичних рівнів електронів у воднево подібних системах знайшла своє підтвердження в квантовій механіці. Квантова механіка також стверджує, що:
a) електрони в атомах водню знаходяться лише в дискретних енергетичних станах. При переході електронів із одних станів в інші випромінюється або поглинається фотон;
б).не існує певних колових орбіт електронів. В силу хвильової природи електрони «розмиті» в просторі подібно до хмарки негативного заряду. Розміри і форму такої хмарки в заданому стані можна розрахувати.
Розглянемо рух електрона в кулонівському полі ядра з зарядом Ze, потенціальна енергія якого виражається формулою
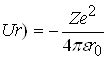 ,
(2.1.1)
,
(2.1.1)
де r - відстань між електроном і ядром.
Стан електрона в атомі водню або воднево подібному атомі описується деякою хвильовою функцією Y, яка задовольняє стаціонарному рівнянню Шредінгера:
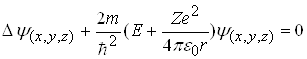 , (2.1.2)
, (2.1.2)
де 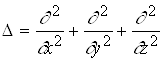 - оператор Лапласа; Е - значення повної енергії електрона в атомі; m - маса частинки;
- оператор Лапласа; Е - значення повної енергії електрона в атомі; m - маса частинки; ![]()
![]() (x,y,z) - хвильова функція в декартові системі координат.
(x,y,z) - хвильова функція в декартові системі координат.
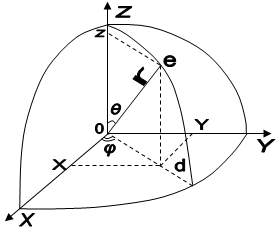 Для розв’язування рівняння Шредінгера (2.1.2), тобто знаходження виду хвильової функції для електрона в атомі водню слід перейти від декартових координат до сферичних. В цьому випадку зв’язок між параметрами цих систем координат визначається з рис.2.1.
Для розв’язування рівняння Шредінгера (2.1.2), тобто знаходження виду хвильової функції для електрона в атомі водню слід перейти від декартових координат до сферичних. В цьому випадку зв’язок між параметрами цих систем координат визначається з рис.2.1.
Рис.2.1.
Співвідношення, які зв’язують координати x,y,z декартової прямокутної системи координат з сферичними координатами r, q, j наступні:
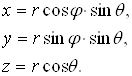 (2.1.3)
(2.1.3)
Таким чином можна вважати, що хвильова функція y електрона в атомі водню залежить від сферичних координат, тобто y=y(r, q, j).
Опустивши не складні, але досить громіздкі перетворення переходу від декартової системи координат до сферичної, одержимо:
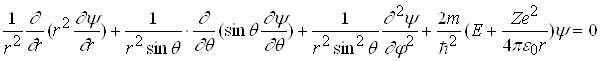 .
.
(2.1.4)
Якщо розглядати основний (не збуджений) стан атома водню, то другою і третьою складовими в рівнянні (2.1.4) можна знехтувати. Електрон в такому стані рухається лише по коловій траєкторії, і хвильова функція не залежить від q і j. Тому
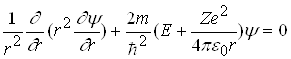 .
(2.1.5)
.
(2.1.5)
Хвильова функція y електрона в основному стані (2.1.5) є функцією лише r, тобто y=y( r). Такий стан називається s-станом; він має сферично-симетричний характер. Імовірність виявити електрон у заданій точці атома - залежатиме лише від r. Умовам стаціонарного стану відповідає легко диференціруєма центральносиметрична функція, яка має вигляд:
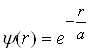 ,
(2.1.6)
,
(2.1.6)
де a - деяка стала величина, яка має розмірність довжини.
Необхідні похідні від (2.1.6) підставимо в (2.1.5). Після скорочення на ![]() одержимо:
одержимо:
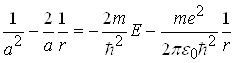 .
(2.1.7)
.
(2.1.7)
Рівність (2.1.7) має місце для будь-яких значень r при виконанні наступних умов:
![]()
 (2.1.8)
(2.1.8)
З рівностей (2.1.8) одержуємо
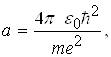 (2.1.9)
(2.1.9)
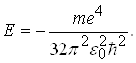 (2.1.10)
(2.1.10)
Покажемо, що вираз (2.1.9) є найбільш імовірною відстанню електрона в атомі водню до ядра. Імовірність знайти електрон на відставні r від ядра, точніше в інтервалі відстаней від r до r+dr, тобто в кульковому шарі з об¢ємом dV=4pr2 dr, дорівнює:
![]() .
(2.1.11)
.
(2.1.11)
З урахуванням (2.1.6), хвильової функції основного стану маємо:
![]() , (2.1.12)
, (2.1.12)
де 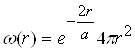 - густина імовірності.
- густина імовірності.
Дослідимо вираз (2.1.12) на максимум, тобто похідну від w(r) прирівняємо до нуля
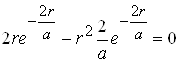 .
.
Звідки
r=a. (2.1.13)
Цей результат є окремим випадком загального висновку: борівські орбіти електрона в атомі водню є геометричними місцями точок, в яких з найбільшою імовірністю можна виявити електрон.
Залежність густини імовірності w(r) виявити електрон на різних відстанях від ядра показана на рис.2.2.
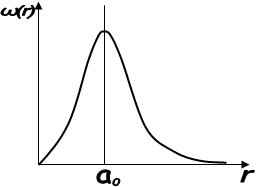
Рис.2.2.
За теорією Бора імовірність виявити електрон у стані з n=1 відмінна від нуля лише для r=a, а згідно з висновками квантової механіки ця відстань є лише найбільш імовірною.
Теорія Бора дає можливість визначити значення енергії електрона в будь-якому енергетичному стані, а також радіус відповідних борівських орбіт:
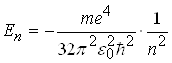 , (2.1.14)
, (2.1.14)
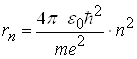 , (2.1.15)
, (2.1.15)
де m - маса електрона; e - заряд електрона; e0 - діелектрична проникність вакууму; ![]() - стала Планка, поділена на 2p; n=1,2,3... - головні квантові числа.
- стала Планка, поділена на 2p; n=1,2,3... - головні квантові числа.
Співставлення (2.1.9) і (2.1.14), а також (2.1.9) і (2.1.15) показують, що висновки квантової механіки і теорії Бора повністю співпадають. Це співподання підкреслює значну історичну роль теорії Бора, яка ще не є квантовою, однак і не класичною теорією.
Хвильові функції для наступних двох енергетичних рівнів електронів в атомі водню мають вигляд
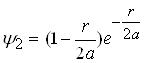 , (2.1.16)
, (2.1.16)
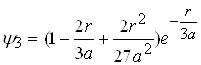 .
(2.1.17)
.
(2.1.17)
Ці хвильові функції також є розв¢язками рівняння (2.1.4) при умові, що ![]() і
і ![]() . Можна показати, що формула (2.1.14) є значенням енергії електрона на будь-якому енергетичному рівні.
. Можна показати, що формула (2.1.14) є значенням енергії електрона на будь-якому енергетичному рівні.
Однак для повного пояснення стану електрона в атомі водню необхідні ще два квантові числа, які входять у відповідні рівняння хвильових функцій і які характеризують момент імпульсу електрона в атомі.
Для збуджених атомів хвильові функції не є центрально симетричними і залежать не лише від r, а і від q і j. Ці хвильові функції містять три цілочислові параметри, які називають квантовими числами. Серед них:
n - головне квантове число, співпадає з аналогічним квантовим числом теорії Бора і набуває значень від 1 до ¥;
l - орбітальне квантове число, квантує момент імпульсу
![]() .
(2.1.18)
.
(2.1.18)
Орбітальне квантове число набуває значень l=0,1,2,... .
ml- магнітне квантове число, квантує проекцію орбітального моменту імпульсу на вісь Z напрямку зовнішнього магнітного поля
![]() .
(2.1.19)
.
(2.1.19)
Магнітне квантове число набуває значень ml= 0,±1,±2,±3... .
Похожие работы
... івнює , а в домішкових напівпровідниках має зміст енергії іонізації донорів чи акцепторів. Отже, питома електропровідність напівпровідників експоненційно збільшується з ростом температури, чим останні принципово відрізняються від металів. Розділ VII. Фізика ядра та елементарних часток. § 7.1. Склад і характеристики ядра Ядро атома, як центральну позитивно заряджену масивну частину атома, ...
... ї й експериментальної фізики, раніше розроблені для вивчення макромолекул небіологічного походження. Неможливо провести границю між молекулярною біофізикою і біофізичною хімією, так само як не можна провести границю між молекулярною фізикою і фізичною хімією. Класифікація областей знання має завжди історичний і не строго визначений характер. Молекулярна фізика і відповідні розділи фізичної хімії ...
... математики. Фізика є теоретичним фундаментом для вивчення професійно-орієнтованих, військово-технічних і військових дисциплін. Тема 1. Кінематика і динаміка матеріальної точки Навчальний потік інженери Час 2 години Місце Навчальна та виховна мета _________________________________________ ____________________________________________________________ Навчальні питання і розподіл часу ...
... на цій же осі. Згідно Френелю, дія такої перешкоди зводиться до того, що екран якби усуває ту частину хвильового фронту, яку він прикриває. На відкритій же частині світлове поле не змінюється. Це наближення геометричної оптики, а тому воно виконується, якщо радіус отвору >> Визначимо розміри і число зон Френеля, що вкладаються в отвір Нехай - діаметр отвору, а та віддалені від його ...

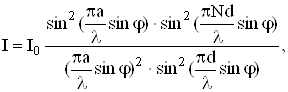
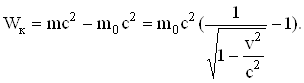


0 комментариев