Навигация
Енергія атома водню і його спектр. Виродження рівнів
2.1.2. Енергія атома водню і його спектр. Виродження рівнів.
Правила відбору.
Знаючи кількісне співвідношення для енергії електрона на енергетичному рівні в атомі водню, можна розрахувати весь його спектр. Нехай енергія більш високого збудженого енергетичного рівня дорівнює
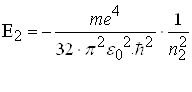 (2.1.19)
(2.1.19)
а енергія нижчого рівня
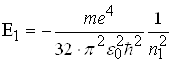 (2.1.19)
(2.1.19)
Частоти, які відповідають різним спектральним лініям, можна записати у вигляді
![]() ,
,
або
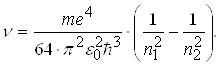 (2.1.21)
(2.1.21)
Серія спектральних ліній, яким відповідає n1=1, називається серією Лаймана. Всі лінії цієї серії розміщені в ультрафіолетовій області спектра електромагнітного випромінювання. У випадку, коли n1=2, виникає друга серія випромінювання, яка називається серією Бальмера. Перші чотири лінії цієї серії знаходяться у видимій області спектра. Інші спектральні лінії цієї серії перебувають на межі видимої і ультрафіолетової області спектра.
Формула (2.1.21) називається формулою Бальмера. У цій формулі вираз перед дужками є сталою величиною, яку називають сталою Рідберга. Стала Рідберга R розрахована з великою точністю. Її величина дорівнює
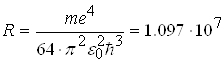 м-1.
м-1.
Число знаків, до яких визначена стала Рідберга показує рівень точності сучасної спектроскопії і ілюструє повне співпадання розрахунків за формулою Бальмера з результатами спостережень.
Якщо n1=3, то за формулою (2.1.21) можна розрахувати наступну серію випромінювання - серію Пашена. Всі лінії цієї серії перебувають в інфрачервоній області спектра.
Наступна серія випромінювання для n1=4 носить назву серії Бреккета. Лінії цієї серії перебувають в інфрачервоній області спектра.
Характер утворення спектральних серій атомом водню наведено на рис. 2.3.
Кожному значенню енергії електрона в атомі водню En (за винятком Е1) відповідає декілька значень хвильової функції ![]() . Вони відрізняються значеннями квантових чисел l i ml. Це означає, що атом водню може мати однакове значення енергії і перебувати в кількох різних квантових станах.
. Вони відрізняються значеннями квантових чисел l i ml. Це означає, що атом водню може мати однакове значення енергії і перебувати в кількох різних квантових станах.
Стани з однаковою енергією називаються виродженими, а число таких станів з одним значенням енергії, називається порядком виродження.
Порядок виродження легко обчислити виходячи з числа можливих значень l i ml. Кожному значенню числа n відповідає 2l+1 значень квантового числа ml. Тому число різноманітних станів для даного значення n, дорівнює
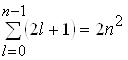 (2.1.22)
(2.1.22)
Таким чином кожен рівень енергії атома водню має порядок виродження 2n2.
В квантовій механіці доводиться, що можливі лише такі переходи електронів між енергетичними рівнями, для яких виконується умова зміни орбітального квантового числа l на одиницю:
Dl=±1 . (2.1.23)
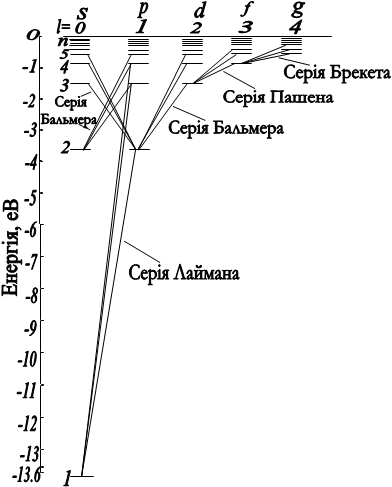
Рис. 2.3.
Умова, яка виражена співвідношенням (2.1.23) називається правилом відбору. Існування цього правила обумовлено тим, що фотон має власний момент імпульсу, який називають спіном, рівним наближено ![]() . При випромінюванні фотон забирає від атома цей момент, а при поглинанні віддає атому. Тому правило відбору є відповідним наслідком закону збереження моменту імпульсу.
. При випромінюванні фотон забирає від атома цей момент, а при поглинанні віддає атому. Тому правило відбору є відповідним наслідком закону збереження моменту імпульсу.
Переходи електронів в атомі водню, які дозволені правилом відбору показані на рис. 2.3.
Серії Лаймана відповідають переходи
np®1s, (n=2,3,4,...).
Серії Бальмера відповідають переходи
np®2s, ns®2p i nd®2p, (n=3,4,5,...).
Стан 1s є основним станом атому водню. В цьому стані атом має найменшу енергію. Для виведення атома з основного стану йому слід надати необхідної енергії за рахунок зовнішнього джерела. Таким джерелом енергії може бути нагрівання, електричний розряд або опромінення.
При опромінені водню фотонами від зовнішнього джерела їх енергія поглинається повністю лише у випадку коли енергія фотонів в точності співпадає з різницею енергії двох енергетичних рівнів. В цьому випадку фотон зникає повністю, передаючи атому всю свою енергію. Атом не може поглинути частину фотона, так як фотон є неподільним.
2.1..3. Механічний і магнітний моменти атома водню.
Орбітальне квантове число l визначає стан електрона в атомі. Якщо рух електрона характеризується значенням квантового числа l=0, то електрон перебуває в s- стані, а сам електрон називається s-електроном. Квантовому числу l=1 відповідає р-стан електрона, l=2 - d-стан, l=3 - f-стан і т. д.
Для електрона, що знаходиться в атомі водню на n-му енергетичному рівні, можливі одна колова орбіта при l=n-1 i n-1 еліптичних орбіт. Із зменшенням l збільшується ступінь витягнутості орбіти. Отже, при заданому головному квантовому числі орбітальне квантове число l визначає форму орбіти.
У квантовій механіці орбітальний момент імпульсу електрона визначається таким співвідношенням:
![]() , де (l=0,1,2,...n-1). (2.1.24)
, де (l=0,1,2,...n-1). (2.1.24)
Цей вираз свідчить про можливість таких рухів електрона, для яких (при l=0) орбітальний момент імпульсу електрона дорівнює нулю.
Третє квантове число ml, яке називається магнітним квантовим числом, визначає просторовий розподіл траєкторії руху електрона, а також і проекцію вектора механічного моменту або моменту імпульсу орбіти на заданий напрям.
Орбіту, по якій рухається електрон, можна розглядати як контур струму. Такий контур характеризується певним значенням орбітального магнітного моменту електрона ![]() , векторною величиною, що направлена вздовж осі орбіти в той бік, куди направлена індукція магнітного поля, створюваного цим контуром. Між вектором
, векторною величиною, що направлена вздовж осі орбіти в той бік, куди направлена індукція магнітного поля, створюваного цим контуром. Між вектором ![]() і
і ![]() існує наступний зв’язок
існує наступний зв’язок
![]() = -
= - 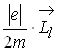 =-g
=-g![]() , (2.1.25)
, (2.1.25)
де е - заряд електрона; m - маса електрона; g![]() - гіромагнітне відношення.
- гіромагнітне відношення.
Враховуючи значення Ll з (2.1.24) одержимо:
![]() =-g
=-g ![]() =-
=-![]() б
б![]() , (2.1.26)
, (2.1.26)
де ![]() б=g
б=g![]() - магнетон Бора.
- магнетон Бора.
Як видно з (2.1.26) вектори ![]() і
і ![]() мають протилежні напрямки.
мають протилежні напрямки.
Вектор ![]() може мати 2l+1 просторових орієнтацій, а це означає, що при даному l електрон в атомі, який вміщено в зовнішнє магнітне поле, може рухатися по 2l+1 орбітах, які відрізняються своєю орієнтацією щодо напрямку магнітного поля.
може мати 2l+1 просторових орієнтацій, а це означає, що при даному l електрон в атомі, який вміщено в зовнішнє магнітне поле, може рухатися по 2l+1 орбітах, які відрізняються своєю орієнтацією щодо напрямку магнітного поля.
![]() , (2.1.27)
, (2.1.27)
де ml - магнітне квантове число.
На рис. 2.4. зображено можливі значення проекції орбітального механічного моменту на напрям осі z зовнішнього магнітного поля для випадків l=1 i l=2.
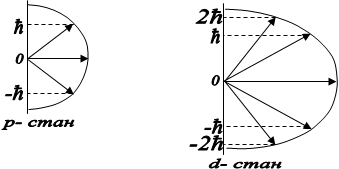
Рис. 2.4.
Таким чином просторове квантування приводить до розчеплення в магнітному полі енергетичного рівня електрона на ряд підрівнів, а отже, і до розчеплення спектральних ліній. Таке явище спостерігав Зеєман. Розчеплення спектральних ліній також можливе в електричному полі - дослід Штарка.
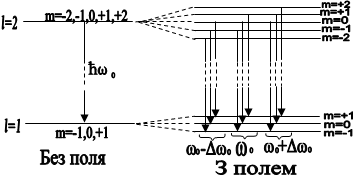
Рис. 2.5
Між розщепленими рівнями можливі переходи електронів згідно правил відбору (рис. 2.5)
Dl=±1 i Dml=0 ; ±1.
2.2 Багатоелектронні атоми.
2.2.1. Досліди Штерна і Герлаха. Спін електрона.
2.2.2. Принцип нерозрізненості тотожних частинок. Принцип
Паулі.
2.2.3. Розподіл електронів за станами. Періодична система
елементів.
2.2.4. Рентгенівські промені. Суцільний спектр і його межі.
Характеристичний спектр. Закон Мозлі.
2.2.1. Досліди Штерна і Герлаха. Cпін електрона
Висновки квантової механіки про просторове квантування потребували експериментального підтвердження . Виявилось, що всі електронні лінії мають так звану «тонку структуру», яка спостерігається навіть при відсутності зовнішнього магнітного поля. Так, всі спектральні лінії водню і лужних металів є дублетами, тобто складаються з двох окремих, близько розташованих ліній. Була висунута гіпотеза про наявність у електронів власного механічного моменту, пов’язаного з обертанням його навколо власної осі. Пізніше власний механічний момент електронів S назвали спіном. Чисельно спін електрона дорівнює 1/2![]() . Електрону властивий також магнітний момент, що дорівнює магнетону Бора mБ=
. Електрону властивий також магнітний момент, що дорівнює магнетону Бора mБ=![]() g, де g - гіромагнітне відношення, рівне e/2m; Власний механічний і магнітний моменти електрона можуть бути орієнтовані лише двома способами: паралельно або антипаралельно відносно вибраного напрямку. Ці дві орієнтації визначаються четвертим квантовим числом, яке називається спіновим. Спінове квантове число може набувати значень 1/2 і -1/2 . Отже, на ряду з уже введеними раніше трьома квантовими числами n, l, ml є ще четверте квантове число ms - яке квантує власний механічний момент електрона.
g, де g - гіромагнітне відношення, рівне e/2m; Власний механічний і магнітний моменти електрона можуть бути орієнтовані лише двома способами: паралельно або антипаралельно відносно вибраного напрямку. Ці дві орієнтації визначаються четвертим квантовим числом, яке називається спіновим. Спінове квантове число може набувати значень 1/2 і -1/2 . Отже, на ряду з уже введеними раніше трьома квантовими числами n, l, ml є ще четверте квантове число ms - яке квантує власний механічний момент електрона.
Гіпотезу про існування власного механічного моменту (спіну) і власного магнітного моменту було пояснено в дослідах Штерна і Герлаха, виконаних ними ще в 1921-1923р.р.
Для дослідження були використані нейтральні атоми срібла, на зовнішніх оболонках яких рухається по одному електрону. Схема установки дослідів Штерна і Герлаха показана на рис. 2.6.
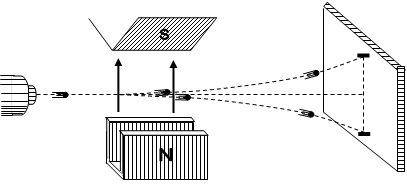
Рис. 2.6
В установці на рис. 2.6. було створено досить неоднорідне магнітне поле за рахунок особливої конструкції магнітних полюсів постійного магніту.
Потенціальна енергія атомів срібла пов’язана з Рм і В співвідношенням
![]() (2.1.28)
(2.1.28)
де ![]() - вектор магнітного моменту атому срібла:
- вектор магнітного моменту атому срібла:
![]() - вектор індукції зовнішнього магнітного поля.
- вектор індукції зовнішнього магнітного поля.
Якщо зовнішнє магнітне поле буде постійним, то магнітні моменти атомів срібла, здійснювали б прецесію навколо вектора ![]() , а магнітні сили були б відсутні.
, а магнітні сили були б відсутні.
В сильно неоднорідному магнітному полі цього не спостерігається, так як
 , тому що
, тому що ![]()
Отже
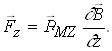 (2.1.29)
(2.1.29)
Під дією цієї магнітної сили (2.1.29.) повинно бути розчеплення спектральних рівнів.
Якщо просторового квантування немає, тобто орієнтація магнітних моментів атомів у зовнішньому магнітному полі довільна, то на екрані спостерігатиметься неперервний розподіл атомів. При просторовому квантуванні пучок атомів після проходження неоднорідного поля розчеплюється на кілька пучків. Таке розчеплення атомних пучків спостерігали Штерн і Герлах і тим самим довели справедливість положення про просторове квантування магнітних моментів атомів. Проте виявилося, що в окремих дослідах є розбіжність між результатами експерименту і вимогами теорії.
Так, в експерименті з атомами срібла спостерігалось розчеплення пучка атомів, що проходили неоднорідне магнітне поле на два пучки, тоді як за теорією ці атоми не повинні зазнавати дії магнітного поля, оскільки їх орбітальні магнітні моменти в основному стані дорівнюють нулю.
Аномальне розчеплення атомних пучків водню, літію, срібла на два пучки неоднорідним магнітним полем пов’язане з квантуванням власного магнітного моменту атомів.
![]() (2.1.30)
(2.1.30)
де ms - спінове квантове число, рівне 1/2 і -1/2.
В дослідах Штерна і Герлаха було встановлено, що власний магнітний момент електронів дорівнює
![]() (2.1.31)
(2.1.31)
Спінове гіромагнітне відношення в два рази перевищує орбітальне. Наявність власного механічного моменту електрона заборонена теорією відносності. Це говорить про те, що класичної інтерпретації власний механічний момент немає.
З квантової точки зору цю властивість частинок називають спіном, і інтерпретують як невід’ємну властивість елементарних частинок.
Спін та власний магнітний момент мають протони, нейтрони та інші елементарні частинки.
Похожие работы
... івнює , а в домішкових напівпровідниках має зміст енергії іонізації донорів чи акцепторів. Отже, питома електропровідність напівпровідників експоненційно збільшується з ростом температури, чим останні принципово відрізняються від металів. Розділ VII. Фізика ядра та елементарних часток. § 7.1. Склад і характеристики ядра Ядро атома, як центральну позитивно заряджену масивну частину атома, ...
... ї й експериментальної фізики, раніше розроблені для вивчення макромолекул небіологічного походження. Неможливо провести границю між молекулярною біофізикою і біофізичною хімією, так само як не можна провести границю між молекулярною фізикою і фізичною хімією. Класифікація областей знання має завжди історичний і не строго визначений характер. Молекулярна фізика і відповідні розділи фізичної хімії ...
... математики. Фізика є теоретичним фундаментом для вивчення професійно-орієнтованих, військово-технічних і військових дисциплін. Тема 1. Кінематика і динаміка матеріальної точки Навчальний потік інженери Час 2 години Місце Навчальна та виховна мета _________________________________________ ____________________________________________________________ Навчальні питання і розподіл часу ...
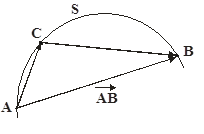
... на цій же осі. Згідно Френелю, дія такої перешкоди зводиться до того, що екран якби усуває ту частину хвильового фронту, яку він прикриває. На відкритій же частині світлове поле не змінюється. Це наближення геометричної оптики, а тому воно виконується, якщо радіус отвору >> Визначимо розміри і число зон Френеля, що вкладаються в отвір Нехай - діаметр отвору, а та віддалені від його ...

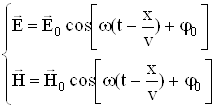
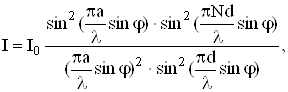


0 комментариев