Навигация
Основы математического анализа
17907
знаков
0
таблиц
3
изображения
1. Множества и операции над множествами
Напомним основные обозначения, понятия, относящиеся к множествам, которых будем придерживаться дальше.
Начнем с основного понятия, которое встречается практически в каждом разделе математики - это понятие множества.
Множество - это совокупность, набор элементов, объединенных общими свойствами.
Множества обозначаются заглавными латинскими буквами 
, а элементы множества строчными латинскими буквами 
.
Запись 
означает, что есть множество 
с элементами 
, которые связаны между собой какой-то функцией 
.
Замечание. Элементы в множество входят по одному разу, т.е. без повторений.
Основные операции:
1. Принадлежность элемента множеству:
где 
-- элемент и -- множество (элемент принадлежит множеству ).
2. Непринадлежность элемента множеству:
где -- элемент и -- множество (элемент не принадлежит множеству ).
3. Объединение множеств: 
.
Объединением двух множеств и 
называется множество 
, которое состоит из элементов множеств и , т.е.
или 
4. Пересечение множеств: 
.
Пересечением двух множеств и называется множество , которое состоит из общих элементов множеств и , т.е.
и
5. Разность множеств: 
.
Разностью двух множеств и , например, множество минус множество , называется множество , которое состоит из элементов множества , которых нет в множестве , т.е.
и 
6. Симметрическая разность множеств:
.
Симметрической разностью двух множеств и называется множество , которое состоит из не общих элементов множеств и , т.е.
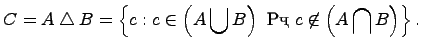
7. Дополнение множества: 
.
Если предположим, что множество является подмножеством некоторого универсального множества 
, тогда определяется операция дополнения:
и
8. Вхождение одного множества в другое множество: 
.
Если любой элемент множества является элементом множества , то говорят, что множество есть подмножество множества (множество входит в множество ).
9. Не вхождение одного множества в другое множество: 
.
Если существует элемент множества , который не является элементом множества , то говорят, что множество не подмножество множества (множество не входит в множество ).
Похожие работы
... y = 0 корней не имеет, , , х = 1/5 – асимптота y(0.007) = -0.3 5. y(0.4 + 4πk) = 4.9 + 48πk y(-0.4 + 4πk) = -4.9 + 48πk , знак совпадает со знаком ctg(x/2) Литература 1. Зорич В.А. Математический анализ. Ч. 1, М., 2001. Ч. 2. 2001. 2. Ильин В.А., Позняк Э.Г. Основы ...
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
... задатков) Как следует организовать и проводить обучение, с тем чтобы, учитывая все эти факторы, вести за собой умственное развитие ребенка, является весьма сложной и до конца еще не решенной психолого-педагогической проблемой. Другие аспекты развития мышления в процессе обучения (развитие логического мышления, мотивация мышления, мышление и решение задач и др.) мы еще рассмотрим в своей работе. ...
0 комментариев