Навигация
1. P(m) справедливо;
2. P(n) будучи истинным предложением, влечет истинность предложения P(n + 1) для любого натурального n, n ≥ m, тогда P(n) - истинное предложение для любого натурального n, n ≥ m.
В дальнейшем рассмотрим примеры применения метода математической индукции.
Пример 1. Доказать следующие равенства
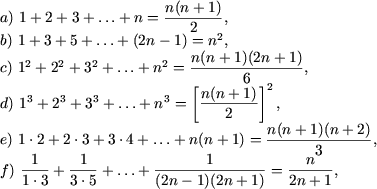
g) формула бинома Ньютона:
![]()
где n Î N.
Решение. a) При n = 1 равенство примет вид ![]() 1=1, следовательно, P(1) истинно. Предположим, что данное равенство справедливо, то есть, имеет место
1=1, следовательно, P(1) истинно. Предположим, что данное равенство справедливо, то есть, имеет место
![]() .
.
Следует проверить (доказать), что P(n + 1), то есть
![]()
истинно. Поскольку (используется предположение индукции)
![]()
получим
![]()
то есть, P(n + 1) - истинное утверждение.
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
Замечание 2. Этот пример можно было решить и иначе. Действительно, сумма 1 + 2 + 3 + ... + n есть сумма первых n членов арифметической прогрессии с первым членом a1 = 1 и разностью d = 1. В силу известной формулы ![]() , получим
, получим
![]()
b) При n = 1 равенство примет вид: 2·1 - 1 = 12 или 1=1, то есть, P(1) истинно. Допустим, что имеет место равенство
1 + 3 + 5 + ... + (2n - 1) = n2
и докажем, что имеет место P(n + 1):
1 + 3 + 5 + ... + (2n - 1) + (2(n + 1) - 1) = (n + 1)2
или
1 + 3 + 5 + ... + (2n - 1) + (2n + 1) = (n + 1)2.
Используя предположение индукции, получим
1 + 3 + 5 + ... + (2n - 1) + (2n + 1) = n2 + (2n + 1) = (n + 1)2.
Таким образом, P(n + 1) истинно и, следовательно, требуемое равенство доказано.
Замечание 3. Этот пример можно решить (аналогично предыдущему) без использования метода математической индукции.
c) При n = 1 равенство истинно: ![]() 1=1. Допустим, что истинно равенство
1=1. Допустим, что истинно равенство
![]()
и покажем, что
![]()
то есть истинность P(n) влечет истинность P(n + 1). Действительно,
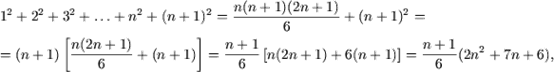
и, так как 2n2 + 7n + 6 = (2n + 3)(n + 2), получим
![]()
и, следовательно, исходное равенство справедливо для любого натурального n.
d) При n = 1 равенство справедливо: ![]() 1=1. Допустим, что имеет место
1=1. Допустим, что имеет место
![]()
и докажем, что
![]()
Действительно,
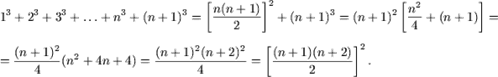
e) Утверждение P(1) справедливо: ![]() 2=2. Допустим, что равенство
2=2. Допустим, что равенство
![]()
справедливо, и докажем, что оно влечет равенство
![]()
Действительно,
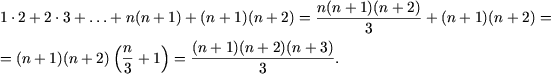
Следовательно, исходное равенство имеет место для любого натурального n.
f) P(1) справедливо: ![]() 1/3 = 1/3. Пусть имеет место равенство P(n):
1/3 = 1/3. Пусть имеет место равенство P(n):
![]() .
.
Покажем, что последнее равенство влечет следующее:
![]()
Действительно, учитывая, что P(n) имеет место, получим
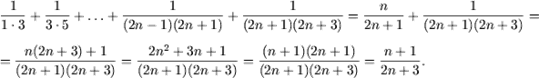
Таким образом, равенство доказано.
g) При n = 1 имеем a + b = b + a и, следовательно, равенство справедливо.
Пусть формула бинома Ньютона справедлива при n = k, то есть,
![]()
Тогда
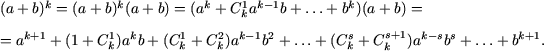
Используя равенство ![]() получим
получим
![]()
Пример 2. Доказать неравенства
a) неравенство Бернулли: (1 + )n ≥ 1 + n, > -1, n N.
b) x1 + x2 + ... + xn ≥ n, если x1x2· ... ·xn = 1 и xi > 0, ![]() .
.
c) неравенство Коши относительно среднего арифемтического и среднего геометрического
![]() где xi > 0,
где xi > 0, ![]() , n ≥ 2.
, n ≥ 2.
d) sin2na + cos2na ≤ 1, n Î N.
e) ![]()
f) 2n > n3, n Î N, n ≥ 10.
Решение. a) При n = 1 получаем истинное неравенство
1 + a ≥ 1 + a.
Предположим, что имеет место неравенство
(1 + a)n ≥ 1 + na (1)
и покажем, что тогда имеет место и
(1 + a)n + 1 ≥ 1 + (n + 1)a.
Действительно, поскольку a > -1 влечет a + 1 > 0, то умножая обе части неравенства (1) на (a + 1), получим
(1 + a)n(1 + a) ≥ (1 + na)(1 + a)
или
(1 + a)n + 1 ≥ 1 + (n + 1)a + na2
Поскольку na2 ≥ 0, следовательно,
(1 + a)n + 1 ≥ 1 + (n + 1)a + na2 ≥ 1 + (n + 1)a.
Таким образом, если P(n) истинно, то и P(n + 1) истинно, следовательно, согласно принципу математической индукции, неравенство Бернулли справедливо.
b) При n = 1 получим x1 = 1 и, следовательно, x1 ≥ 1 то есть P(1) - справедливое утверждение. Предположим, что P(n) истинно, то есть, если adica, x1,x2,...,xn - n положительных чисел, произведение которых равно единице, x1x2·...·xn = 1, и x1 + x2 + ... + xn ≥ n.
Покажем, что это предложение влечет истинность следующего: если x1,x2,...,xn,xn+1 - (n + 1) положительных чисел, таких, что x1x2·...·xn·xn+1 = 1, тогда x1 + x2 + ... + xn + xn + 1 ≥ n + 1.
Рассмотрим следующие два случая:
1) x1 = x2 = ... = xn = xn+1 = 1. Тогда сумма этих чисел равна (n + 1), и требуемое неравество выполняется;
2) хотя бы одно число отлично от единицы, пусть, например, больше единицы. Тогда, поскольку x1x2· ... ·xn·xn + 1 = 1, существует еще хотя бы одно число, отличное от единицы (точнее, меньше единицы). Пусть xn + 1 > 1 и xn < 1. Рассмотрим n положительных чисел
x1,x2,...,xn-1,(xn·xn+1).
Произведение этих чисел равно единице, и, согласно гипотезе,
x1 + x2 + ... + xn-1 + xnxn + 1 ≥ n.
Последнее неравенство переписывается следующим образом:
x1 + x2 + ... + xn-1 + xnxn+1 + xn + xn+1 ≥ n + xn + xn+1
или
x1 + x2 + ... + xn-1 + xn + xn+1 ≥ n + xn + xn+1 - xnxn+1.
Поскольку
(1 - xn)(xn+1 - 1) > 0,
n + xn + xn+1 - xnxn+1 = n + 1 + xn+1(1 - xn) - 1 + xn = = n + 1 + xn+1(1 - xn) - (1 - xn) = n + 1 + (1 - xn)(xn+1 - 1) ≥ n + 1.
Следовательно,
x1 + x2 + ... + xn + xn+1 ≥ n+1,
то есть, если P(n) справедливо, то и P(n + 1) справедливо. Неравенство доказано.
Замечание 4. Знак равенства имеет место тогда и только тогда, когда x1 = x2 = ... = xn = 1.
c) Пусть x1,x2,...,xn - произвольные положительные числа. Рассмотрим следующие n положительных чисел:
![]()
Поскольку их произведение равно единице:
![]()
согласно ранее доказанному неравенству b), следует, что
![]()
откуда
![]()
Замечание 5. Равенство выполняется если и только если x1 = x2 = ... = xn.
d) P(1) - справедливое утверждение: sin2a + cos2a = 1. Предположим, что P(n) - истинное утверждение:
sin2na + cos2na ≤ 1
и покажем, что имеет место P(n + 1). Действительно,
sin2(n + 1)a + cos2(n + 1)a = sin2na·sin2a + cos2na·cos2a < sin2na + cos2na ≤ 1
(если sin2a ≤ 1, то cos2a < 1, и обратно: если cos2a ≤ 1, то sin2a < 1). Таким образом, для любого n Î N sin2na + cos2n ≤ 1 и знак равенства достигается лишь при n = 1.
e) При n = 1 утверждение справедливо: ![]() 1 < 3/2.
1 < 3/2.
Допустим, что ![]() и докажем, что
и докажем, что
![]()
Поскольку
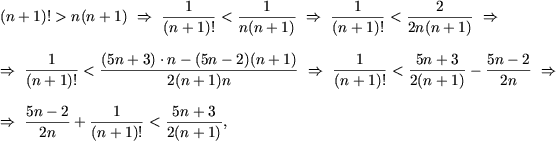
учитывая P(n), получим
![]()
f) Учитывая замечание 1, проверим P(10): 210 > 103, 1024 > 1000, следовательно, для n = 10 утверждение справедливо. Предположим, что 2n > n3 (n > 10) и докажем P(n + 1), то есть 2n+1 > (n + 1)3.
Поскольку при n > 10 имеем ![]() или
или ![]() , следует, что
, следует, что
2n3 > n3 + 3n2 + 3n + 1 или n3 > 3n2 + 3n + 1.
Учитывая неравенство (2n > n3), получим
2n+1 = 2n·2 = 2n + 2n > n3 + n3 > n3 + 3n2 + 3n + 1 = (n + 1)3.
Таким образом, согласно методу математической индукции, для любого натурального n Î N, n ≥ 10 имеем 2n > n3.
Пример 3. Доказать, что для любого n Î N
a) n(2n2 - 3n + 1) делится на 6,
b) 62n-2 + 3n+1 + 3n-1 делится на 11.
Решение. a) P(1) - истинное утверждение (0 делится на 6). Пусть P(n) справедливо, то есть n(2n2 - 3n + 1) = n(n - 1)(2n - 1) делится на 6. Покажем, что тогда имеет место P(n + 1), то есть, (n + 1)n(2n + 1) делится на 6. Действительно, поскольку
n(n + 1)(2n + 1) = n(n - 1 + 2)(2n - 1 + 2) = (n(n - 1) + 2n)(2n - 1 + 2) =
= n(n - 1)(2n - 1) + 2n(n - 1) + 2n(2n + 1) = n(n - 1)(2n - 1) + 2n·3n =
= n(n - 1)(2n - 1) + 6n2
и, как n(n - 1)(2n - 1), так и 6n2 делятся на 6, тогда и их сумма n(n + 1)(2n + 1) делится 6.
Таким образом, P(n + 1) - справедливое утверждение, и, следовательно, n(2n2 - 3n + 1) делится на 6 для любого n N.
b) Проверим P(1): 60 + 32 + 30 = 11, следовательно, P(1) - справедливое утверждение. Следует доказать, что если 62n-2 + 3n+1 + 3n-1 делится на 11 (P(n)), тогда и 62n + 3n+2 + 3n также делится на 11 (P(n + 1)). Действительно, поскольку
62n + 3n+2 + 3n = 62n-2+2 + 3n+1+1 + 3n-1+1 =
= 62·62n-2 + 3·3n+1 + 3·3n-1 = 3·(62n-2 + 3n+1 + 3n-1) + 33·62n-2
и, как 62n-2 + 3n+1 + 3n-1, так и 33·62n-2 делятся на 11, тогда и их сумма 62n + 3n+2 + 3n делится на 11. Утверждение доказано.
Несобственные интегралы
Пусть функция f(x) определена на полуинтервале (a, b] и ![]() ,
, ![]() ; кроме того
; кроме того
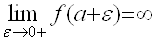
Определение: Несобственным интегралом 1рода от f(x) на (a, b] называется предел:

если этот предел существует. В этом случае говорят, что несобственный интеграл сходится.
Пример:

Если a = 1, то
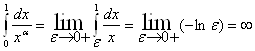
Следовательно, при a < 1 интеграл
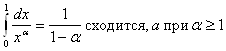

Аналогично определяется несобственный интеграл, если

Определение несобственного интеграла 2 рода:
Пусть ![]() :
: ![]() и существует предел:
и существует предел:
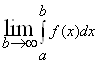
Тогда этот предел называется несобственным интегралом 2 рода, т.е.
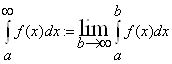
Пример:
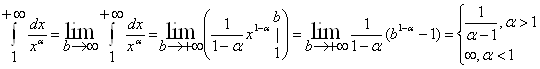
Если a = 1, то

Следовательно, несобственный интеграл
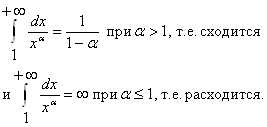
Для исследования сходимости и расходимости несобственных интегралов применяется признак сравнения:
Пусть функция f(x) и g(x) удовлетворяют неравенству: ![]() и несобственный интеграл
и несобственный интеграл 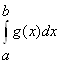 сходится. Тогда сходится и несобственный интеграл
сходится. Тогда сходится и несобственный интеграл 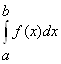 .
.
Доказательство: В силу сходимости 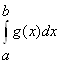 по критерию Коши для функции
по критерию Коши для функции ![]() , выполняется неравенство
, выполняется неравенство 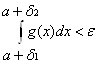 . Но тогда, ввиду неравенств:
. Но тогда, ввиду неравенств: ![]() аналогично неравенство будет справедливо и для функции f(x), т.е.
аналогично неравенство будет справедливо и для функции f(x), т.е.
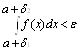
Следовательно, по критерию Коши существует предел:
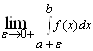 ,
,
т.е. этот интеграл сходится.
Замечание1: Аналогичный признак сравнения справедлив и для несобственных интегралов 2 рода.
Замечание2: Отрицанием признака сравнения будет следующее утверждение: если несобственный интеграл 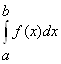 расходится, то расходится и несобственный интеграл
расходится, то расходится и несобственный интеграл
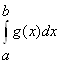 .
.
Эйлеровы интегралы G(a) и B(a, b).
Определим функцию G(a) равенством:
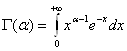 .
.
Покажем, что интеграл сходится при a > 0. Представим этот интеграл в виде суммы двух интегралов:
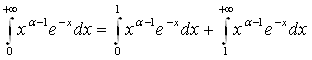
и докажем сходимость каждого из этих интегралов при a > 0.
Обозначим
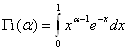 и
и ![]() .
.
Если xÎ(0, 1], то: ![]() . Так как интеграл
. Так как интеграл 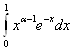 , как это было доказано выше сходится при 1 - a< 1, т.е. при a>0, то по признаку сравнения интеграл
, как это было доказано выше сходится при 1 - a< 1, т.е. при a>0, то по признаку сравнения интеграл ![]() сходится при a>0. Если xÎ[1, +
сходится при a>0. Если xÎ[1, + ![]() ) , то для некоторой константы c>0 выполняется неравенство:
) , то для некоторой константы c>0 выполняется неравенство: ![]() .
.
Заметим, что
![]() ,
,
т.е. этот интеграл сходится при любых aÎR. Следовательно, функция Эйлера G(a) = G1(a) + G2(a) определена для всех a>0.
Далее, определим функцию
B(a, b) = 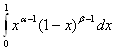
и докажем, что эта функция определена для любых a>0 и b>0.
Обозначим:
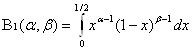 и
и 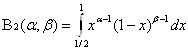 .
.
Если xÎ(0, 1/2], то ![]() . Интеграл
. Интеграл 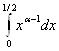 сходится по признаку сравнения 1 - a<1, т.е. при a>0 и при любых значениях b. Заметим, что, если в интеграле B2(a, b) сделать замену t = 1 – x, то мы B1(b, a), который, как мы выяснили, сходится при b>0 и при любых a.
сходится по признаку сравнения 1 - a<1, т.е. при a>0 и при любых значениях b. Заметим, что, если в интеграле B2(a, b) сделать замену t = 1 – x, то мы B1(b, a), который, как мы выяснили, сходится при b>0 и при любых a.
Следовательно, функция Эйлера B(a, b) = B1(a, b) + B2(a, b) определена для любых a>0 и b>0. Отметим (без доказательства) следующие свойства интегралов Эйлера:
1) G(1) = 1
2) G(a + 1) = aG(a), a>0
3) G(n + 1) = n!, nÎN
4) G(a)G(1 - a) =![]() , 0<a<1
, 0<a<1
5) G(1/2) = ![]()
6) B(a, b) = ![]()
Пример:
Вычислить интеграл вероятности
![]() .
.
В силу чётности функции ![]() интеграл вероятности можно представить в виде:
интеграл вероятности можно представить в виде:
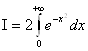 .
.
Сделав в этом интеграле замену t = x2 , получим следующий интеграл:
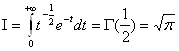
Похожие работы
... y = 0 корней не имеет, , , х = 1/5 – асимптота y(0.007) = -0.3 5. y(0.4 + 4πk) = 4.9 + 48πk y(-0.4 + 4πk) = -4.9 + 48πk , знак совпадает со знаком ctg(x/2) Литература 1. Зорич В.А. Математический анализ. Ч. 1, М., 2001. Ч. 2. 2001. 2. Ильин В.А., Позняк Э.Г. Основы ...
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
... задатков) Как следует организовать и проводить обучение, с тем чтобы, учитывая все эти факторы, вести за собой умственное развитие ребенка, является весьма сложной и до конца еще не решенной психолого-педагогической проблемой. Другие аспекты развития мышления в процессе обучения (развитие логического мышления, мотивация мышления, мышление и решение задач и др.) мы еще рассмотрим в своей работе. ...


0 комментариев