Міністерство освіти і науки України
Донбаський державний технічний університет
Кафедра Вищої Математики
КОНТРОЛЬНА РОБОТАПо дисципліні “Теорія ймовірностей та математична статистика”
Варіант №26
(завдання №14, 2, 4, 12, 11, 15, 2, 14, 3, 6)
Виконала: студентка групи
Перевірила: доцент кафедри вищ. мат.
Алчевськ 2009
РОЗДІЛ I “ТЕОРІЯ ЙМОВІРНОСТЕЙ”
ЗАВДАННЯ №1
14) В урні 2 білі і 3 чорні кульки. Двоє по черзі беруть навмання по одній кульці. Яка імовірність того, що з них перша біла, а друга чорна?
РОЗВ’ЯЗАННЯ
Для білої:
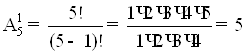
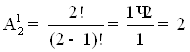
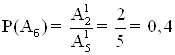
Для чорної:
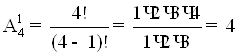
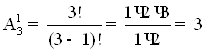

Загальна вірогідність:
![]()
або
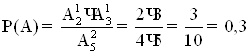
ЗАВДАННЯ №2
2) В першій урні 3 білих і 2 чорних кульки, а в другій 4 білих і 4 чорних кульки. З першої урни в другу навмання перекладають одну кульку, потім з другої урни взяли одну кульку. Яка імовірність, що вона біла?
РОЗВ’ЯЗАННЯ
Вірогідність того, що з першої урни переклали білу кульку:
![]()
Вірогідність того, що з другої урни узяли білу кульку:
![]()
ЗАВДАННЯ №3
4) 4.1 Обчислити ймовірність того, що деяка подія не відбудеться, якщо відомо, що при ![]() випробуваннях вона в середньому відбувається в
випробуваннях вона в середньому відбувається в ![]() випадках.
випадках.
РОЗВ’ЯЗАННЯ
![]()
4.2 З 60 питань, що входять до екзаменаційних білетів, студент підготував 50. Яка ймовірність того, що взятий навмання студентом білет, який містить два питання, буде складатися з підготовлених ним питань?
РОЗВ’ЯЗАННЯ
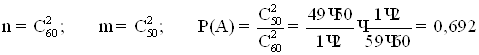
4.3 Яка ймовірність того, що серед вийнятих навмання 4 карт з повної колоди (52 карти), дві виявляться пікової масті?
РОЗВ’ЯЗАННЯ
![]()
ЗАВДАННЯ №4
12) Проведено ![]() незалежних випробувань, в кожному з яких може відбутися подія
незалежних випробувань, в кожному з яких може відбутися подія ![]() з імовірністю
з імовірністю ![]() .
.
I) за локальною теоремою Муавра-Лапласа знайти імовірність того, що подія відбудеться рівно ![]() разів;
разів;
II) за інтегральною теоремою Муавра-Лапласа знайти імовірність того, що подія відбудеться від 700 разів до ![]() разів.
разів.
РОЗВ’ЯЗАННЯ
I) ![]()
1) Скористуємось формулою Муавра-Лапласа:
![]()
2) Знайдемо ![]() :
:
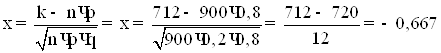
3) Знайдемо ![]() :
:
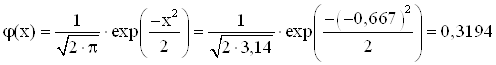
4) Шукана ймовірність:
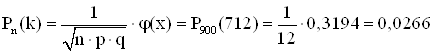
II) ![]()
За інтегральною теоремою Лапласа:

1) Знайдемо межі інтеграла ![]() і
і ![]() :
:
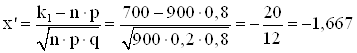

2) Знайдемо функції Лапласа ![]() і
і ![]() :
:
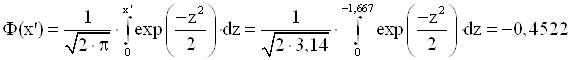
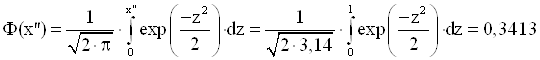
3) Шукана ймовірність:
![]()
ЗАВДАННЯ №5
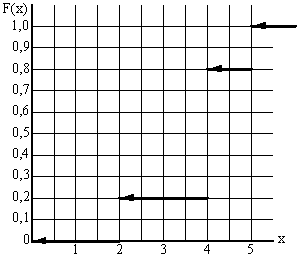
11) Дискретна випадкова величина задана рядом розподілу. Знайти функцію розподілу і побудувати її графік. Знайти математичне сподівання і дисперсію випадкової величини.
| Х | 2 | 4 | 5 |
| Р | 0,2 | 0,6 | 0,2 |
РОЗВ’ЯЗАННЯ
1) Математичне сподівання знайдемо за формулою:
![]()
2) Складемо закон розподілу для ![]() :
:
| Х | 4 | 16 | 25 |
| Р | 0,2 | 0,6 | 0,2 |
![]()
![]()
3) Дисперсію знайдемо за формулою:
![]()
4) Середнє квадратичне відхилення знайдемо за формулою:
![]()
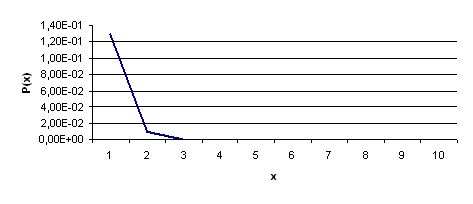
5) Знайдемо функцію розподілу:

6) Графік цієї функції має вигляд:
ЗАВДАННЯ №6
15) Випадкова величина ![]() задана функцією розподілу:
задана функцією розподілу:

Знайти:
I) щільність розподілу ймовірності;
II) математичне сподівання;
III) дисперсію випадкової величини;
IV) імовірність попадання випадкової величини в інтервал ![]() ;
;
V) Накреслити графіки функцій ![]() і
і ![]() .
.
РОЗВ’ЯЗАННЯ
I) щільність розподілу ймовірностей:
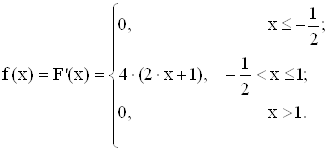
II) математичне сподівання:

III) дисперсія:
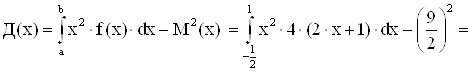
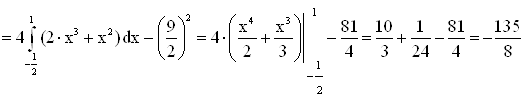
IV) імовірність того, що випадкова величина прийме значення з інтервалу
V) Графіки функцій ![]() і
і ![]() :
:
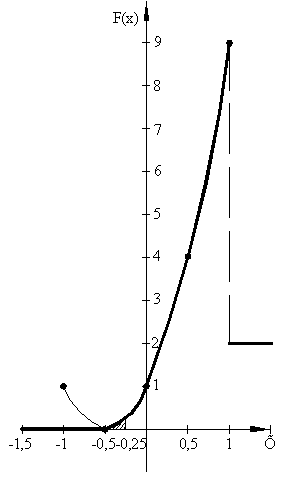
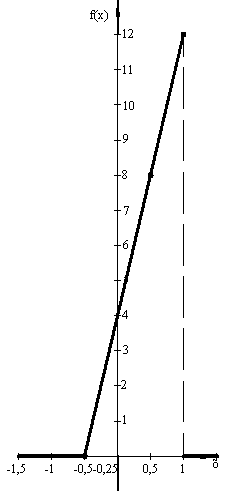
ЗАВДАННЯ №7
2) Відоме математичне сподівання ![]() і дисперсія
і дисперсія ![]() випадкової величини
випадкової величини ![]() .
.
Знайти:
I) імовірність попадання цієї величини в заданий інтервал ![]() ;
;
II) імовірність того, що абсолютна величина відхилення випадкової величини від свого математичного сподівання менша за число ![]() .
.
РОЗВ’ЯЗАННЯ
I) Імовірність влучення випадкової величини ![]() у інтервал
у інтервал ![]() :
:

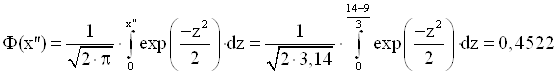
![]()
II) Імовірність того, що абсолютна величина відхилення випадкової величини від свого математичного сподівання буде менше 2, можна обчислити за формулою:
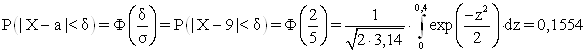
РОЗДІЛ II
14) РОЗРАХУНКОВА РОБОТА №1 “СТАТИСТИЧНИЙ РОЗПОДІЛ ВИБІРКИ”
| 23 | 26 | 31 | 35 | 38 | 43 | 48 | 39 | 36 | 27 |
| 43 | 39 | 37 | 34 | 31 | 27 | 21 | 33 | 32 | 44 |
| 24 | 28 | 30 | 35 | 33 | 39 | 40 | 41 | 46 | 36 |
| 42 | 39 | 35 | 32 | 27 | 29 | 33 | 35 | 38 | 41 |
| 25 | 30 | 30 | 31 | 32 | 34 | 36 | 37 | 38 | 40 |
перший інтервал 21-25
Представити кожну вибірку у вигляді таблиці частот згрупованої вибірки, побудувати гістограму і полігон частот, записати емпіричну функцію розподілу і побудувати їх графік.
РОЗВ’ЯЗАННЯ
1) Складемо таблицю частот згрупованої вибірки:
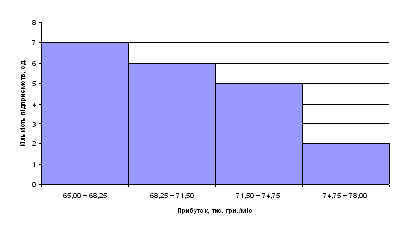
| Межі інтервалу xi | Середина інтервалу xi0 | Частота ni | Накопичувальна частота Σni | Відносна частота ni/n | Накопичувальна відносна частота Σni/n | |
| 21 | 23 | 4 | 4 | 0,08 | 0,08 | |
| 25 | 27 | 6 | 10 | 0,12 | 0,20 | |
| 29 | 31 | 12 | 22 | 0,24 | 0,44 | |
| 33 | 35 | 11 | 33 | 0,22 | 0,66 | |
| 37 | 39 | 11 | 44 | 0,22 | 0,88 | |
| 41 | 43 | 4 | 48 | 0,08 | 0,96 | |
| 45 | 47 | 2 | 50 | 0,04 | 1 |
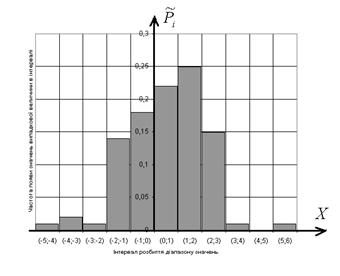
2) Побудуємо гістограму частот:
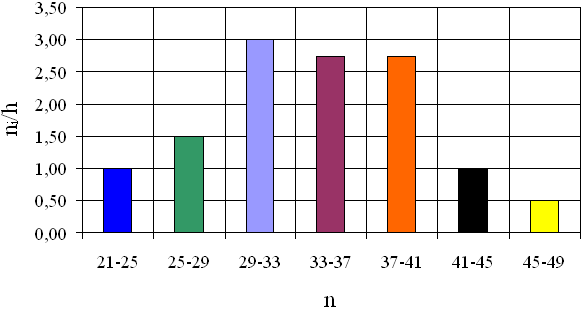
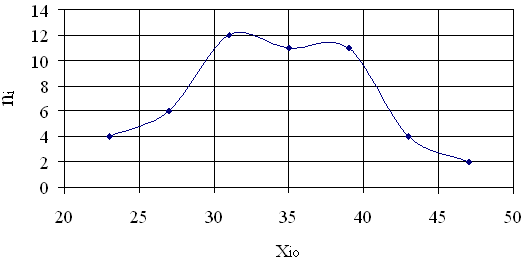
3) Побудуємо полігон частот:
4) Емпірична функція розподілу визначається значеннями накопичувальних відносних частот:

5) Графік розподілу емпіричної функції:
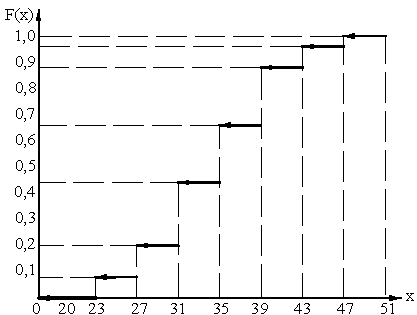
6) Знайдемо методом творів вибіркову середню і вибіркову дисперсію по заданому розподілу вибірки об'єму n=50:
| Середина інтервалу xi0 | 23 | 27 | 31 | 35 | 39 | 43 | 47 |
| Частота ni | 4 | 6 | 12 | 11 | 11 | 4 | 2 |
6.1) Складемо заповнимо таблицю:
| хi0 | ni | Ui | ni×Ui | ni×Ui2 | ni×(Ui+1)2 |
| 23 | 4 | -2 | -8 | 16 | 4 |
| 27 | 6 | -1 | -6 | 6 | 0 |
| 31 | 12 | 0 | 0 | 0 | 12 |
| 35 | 11 | 1 | 11 | 11 | 44 |
| 39 | 11 | 2 | 22 | 44 | 99 |
| 43 | 4 | 3 | 12 | 36 | 64 |
| 47 | 2 | 4 | 8 | 32 | 50 |
| 39 | 145 | 273 | |||
6.2) Обчислимо умовні моменти 1-го і 2-го порядку:

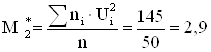
6.3) Знайдемо крок h (різниця між сусідніми інтервалами): ![]() .
.
6.4) Обчислимо шукані, вибіркові, середню дисперсію, враховуючи що помилковий нуль ![]() :
:
![]()
![]()
![]()
3) РОЗРАХУНКОВА РОБОТА №2
“МЕТОД НАЙМЕНЬШИХ КВАДРАТІВ”
За наданими статистичними даними підібрати емпіричну функцію, якщо вона не задана, та:
1. Побудувати діаграму розсіювання.
2. Записати емпіричну функцію.
3. Записати систему нормальних рівнянь.
4. Скласти розрахункову таблицю.
5. Вирішити отриману систему й записати емпіричну функцію зі знайденими параметрами.
Уважаючи, що залежність між змінними ![]() й
й ![]() має вигляд
має вигляд ![]() , знайти оцінки параметрів по наступних вибірках:
, знайти оцінки параметрів по наступних вибірках:
|
| 1 | 3 | 4 | 2 | 5 | 7 | 8 | 9 |
|
| 80 | 90 | 120 | 100 | 110 | 150 | 160 | 130 |
РОЗВ’ЯЗАННЯ
По вибірці спостережень побудуємо в системі координат ![]() и
и ![]() діаграму розсіювання, тобто побудуємо крапки:
діаграму розсіювання, тобто побудуємо крапки:
![]()
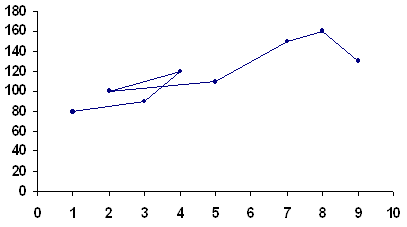
Аналіз дослідницьких даних показує, що в якості емпіричної (підібраної) функції можна використати функцію ![]() . Необхідно знайти параметри а й b, для чого застосуємо МНК. Тоді для визначення параметрів а й b будемо мати систему нормальних рівнянь:
. Необхідно знайти параметри а й b, для чого застосуємо МНК. Тоді для визначення параметрів а й b будемо мати систему нормальних рівнянь:
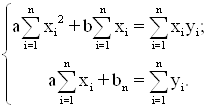
Для зручності обчислень складемо наступну розрахункову таблицю (![]() ):
):
|
|
|
|
|
|
| 1 | 1 | 80 | 1 | 80 |
| 2 | 3 | 90 | 9 | 270 |
| 3 | 4 | 120 | 16 | 480 |
| 4 | 2 | 100 | 4 | 200 |
| 5 | 5 | 110 | 25 | 550 |
| 6 | 7 | 150 | 49 | 1050 |
| 7 | 8 | 160 | 64 | 1280 |
| 8 | 9 | 130 | 81 | 1170 |
|
|
|
|
|
|
Підставимо дані останнього рядка таблиці в нормальну систему рівнянь:

Вирішуючи систему, одержимо ![]() .
.
5) Підставляючи ці значення параметрів, одержимо емпіричну функцію:
![]()
6) РОЗРАХУНКОВА РОБОТА №3
“ЗНАХОДЖЕННЯ ВИБІРКОВОГО КОЕФІЦІЕНТА КОРЕЛЯЦІЇ ТА ПРЯМИХ ЛІНІЙ РЕГРЕСІЇ”
Розподіл 40 заводів кольорової металургії за середньодобовим виробленням металу| |
|
| ||||
| 10-15 | 15-20 | 20-25 | 25-30 | 30-35 | ||
| 2,0-2,5 | 6 | 6 | ||||
| 2,5-3,0 | 6 | 6 | 12 | |||
| 3,0-3,5 | 6 | 4 | 10 | |||
| 3,5-4,0 | 2 | 4 | 2 | 8 | ||
| 4,0-4,5 | 4 | 4 | ||||
|
| 6 | 4 | 8 | 10 | 12 | 40 |
За відповідним рівнянням регресії оцінити середні затрати електроенергії на 1 тн. металу тих заводів, у яких середньодобове вироблення металу складає 22,5 тис.т., та порівняти їх з відповідним груповим середнім.
Надано таблицю, яка визначає деякий неперервний розподіл. За цим розподілом треба утворити дискретний розподіл, взявши значеннями ![]() і
і ![]() середини відповідних інтервалів і припускаючи, що між
середини відповідних інтервалів і припускаючи, що між ![]() і
і ![]() існує лінійна кореляційна залежність, виконати таку роботу:
існує лінійна кореляційна залежність, виконати таку роботу:
1. Обчислити коефіцієнт кореляції та проаналізувати тісноту та напрям зв'язку між ![]() і
і ![]() .
.
2. Скласти рівняння прямих регресії ![]() на
на ![]() та
та ![]() на
на ![]() .
.
3. Обчислити для даного значення однієї змінної відповідне значення іншої, використавши для цього одне з одержаних рівнянь регресії (підхоже) та порівняти це значення з відповідним груповим середнім (це останнє завдання подано разом з кореляційною таблицею).
РОЗВ’ЯЗАННЯ
1) Перейдемо до дискретних розподілів, тобто значення змінних Х и Y приймемо середини відповідних інтервалів:
| |
|
| ||||
| 12,5 | 17,5 | 22,5 | 27,5 | 32,5 | ||
| 2,25 | 6 | 6 | ||||
| 2,75 | 6 | 6 | 12 | |||
| 3,25 | 6 | 4 | 10 | |||
| 3,75 | 2 | 4 | 2 | 8 | ||
| 4,25 | 4 | 4 | ||||
|
| 6 | 4 | 8 | 10 | 12 | 40 |
2) Для обчислення вибіркового коефіцієнта кореляції потрібно обчислити вираження ![]() , для чого скласти кореляційну таблицю в умовних варіантах.
, для чого скласти кореляційну таблицю в умовних варіантах.
За хибний нуль ![]() узята варіанта
узята варіанта ![]() , а за хибний нуль
, а за хибний нуль ![]() узята варіанта
узята варіанта ![]() , які розташовані приблизно в серединах відповідних варіаційних рядів.
, які розташовані приблизно в серединах відповідних варіаційних рядів.
3) У кожній клітці, у якій частота ![]() , записуємо в правому верхньому куті добуток частоти
, записуємо в правому верхньому куті добуток частоти ![]() на
на ![]() .
.
4) Знаходимо суму всіх чисел, що коштують у правих кутах кліток одного рядка й записуємо її в клітку стовпця ![]() .
.
5) Множимо варіанту ![]() на
на ![]() й отриманий добуток записуємо в останню клітку того ж рядка.
й отриманий добуток записуємо в останню клітку того ж рядка.
6) З метою контролю аналогічні обчислення робимо по стовпцях, причому добуток ![]() записуємо в лівому нижньому куті кожної клітки із частотами
записуємо в лівому нижньому куті кожної клітки із частотами ![]() , після чого їх складаємо й отриману суму записуємо в рядок
, після чого їх складаємо й отриману суму записуємо в рядок ![]() .
.
Потім множимо варіанту и на ![]() й результат записуємо в останньому рядку.
й результат записуємо в останньому рядку.
| | -2 | -1 | 0 | 1 | 2 |
|
| |||||||||||
| -2 | -12 | 6 | 12 | 6 | 12 | -24 | ||||||||||||
| -1 | -6 | 6 | 6 | -6 | 6 | 12 | 12 | 18 | -18 | |||||||||
| 0 | 0 | 6 | 0 | 0 | 4 | 4 | 10 | 4 | 0 | |||||||||
| 1 | 2 | 2 | -4 | 4 | 4 | -4 | 2 | 2 | 0 | 8 | -8 | -8 | ||||||
| 2 | 8 | 4 | -8 | 4 | -8 | -16 | ||||||||||||
|
| 6 | 4 | 8 | 10 | 12 | 40 | ||||||||||||
|
| 10 | 4 | 2 | -6 | -18 | |||||||||||||
|
| -20 | -4 | 0 | -6 | -36 | -66 | ||||||||||||
7) Обчислюємо ![]() й
й ![]() :
:
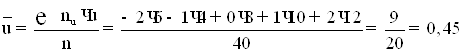
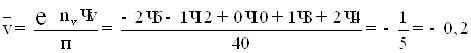
8) Обчислюємо допоміжні величини ![]() й
й ![]() :
:
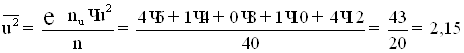
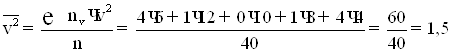
9) Обчислимо ![]() й
й ![]() :
:
![]()
![]()
10) Шуканий вибірковий коефіцієнт кореляції:
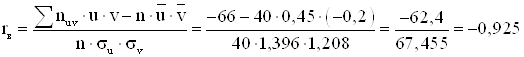
Тому що ![]() , цей зв'язок зворотній.
, цей зв'язок зворотній.
11) Вибіркове рівняння прямої лінії регресії Y на Х має вигляд:
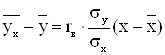 .
.
Обчислимо ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() :
:
![]()
![]()
![]()
![]()
12) Рівняння прямої лінії регресії Y на Х:
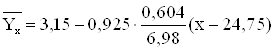
![]()
13) Рівняння прямої лінії регресії Х на Y:
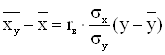
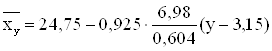
![]()
14) За відповідним рівнянням регресії середнє значення затрат електроенергії на 1 тн. металу тих заводів, у яких середньодобове вироблення металу складає 22,5 тис.т., складає:
![]()
![]()
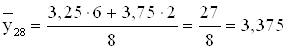
Як видно, узгодження розрахункового і спостережуваного умовних середніх – задовільне.
Похожие работы
... и математическая статистика: Учеб. пособ. для студ. вузов. - 7. изд., стереотип. - М.: Высшая школа, 2001. - 479 с. 3. Задорожня Т.М., Коляда Ю.В., Мамонова Г.В. Збірник задач з теорії ймовірності та математичної статистики (для студентів економічних спеціальностей): Навч. посіб. для студ. вищ. навч. закл. / Державна податкова адміністрація України; Академія держ. податкової служби України. - ...
... Це означає, що оцінки, одержані з використанням нерівності (6), - завищені. Більш точні оцінки можна одержати за допомогою теореми Ляпунова. Список використаної літератури 1. Барковський В.В., Барковська Н.В., Лопатін О.К. теорія ймовірностей та математична статистика. – К.: ЦУЛ, 2002. – 448с. 2. Гмурман В.Е. теория вероятностей и математическая статистика. – М.: Высшая школа, 1980. ...
... ія розподілення експоненціального закону: , а імовірність попадання у інтервал (a,b) безперервної випадкової величини Х, розподіленою за експоненціальним законом дорівнює: . 2. Види типових задач з математичної статистики Тип 1 Ланка дослідів дала певну послідовність результатів. Вирахувати середнє значення виміряння, дисперсію, похибки, а також встановити закони розподілення ...
... Метод моментів Метод моментів є одним із методів точечного оцінювання параметрів розподілу. Нехай закон розподілу випадкової величини X відомий із точністю до числових значень його параметрів 1,2,…,k. Це означає, що відомий вид функції щільності fx(х, ), де = (1,2,…,k), якщо X безперервна (відомий вид функції ймовірності Р (X= х,), якщо X дискретна), але числові значення k параметрів не відомі. ...
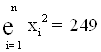
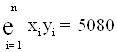
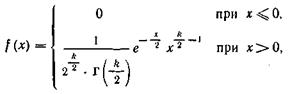
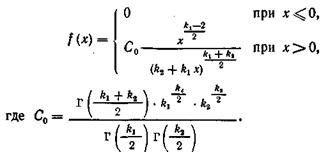

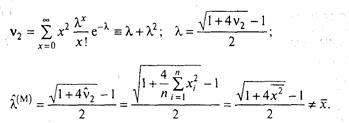
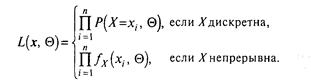
0 комментариев