Навигация
Многомерные и многосвязные системы
Задание Для многомерной системы, заданной матрицами А, В, С, получить:
1. Передаточную функцию ![]() ;
;
2. Частотную передаточную функцию ![]() ;
;
3. Годограф;
4. Импульсную характеристику ![]() ;
;
5. Переходную характеристику ![]() ;
;
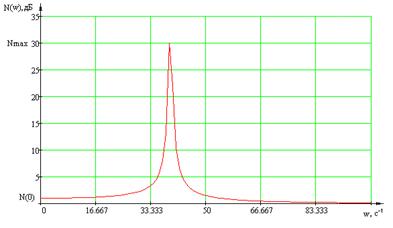
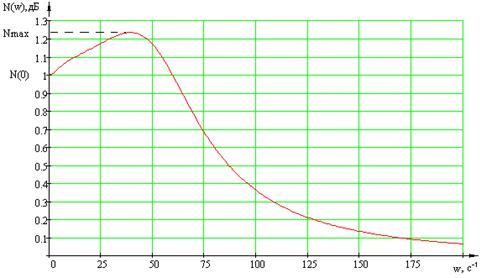
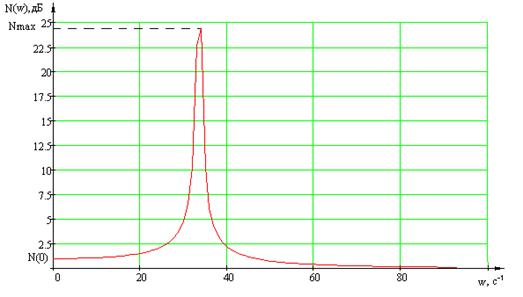
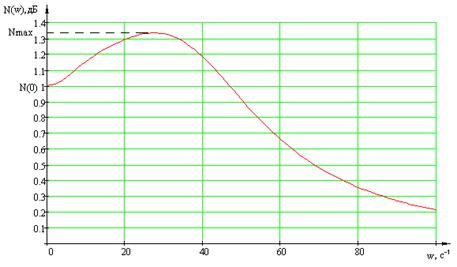
6. ЛАЧХ ![]() ;
;
7. ФЧХ ![]() .
.
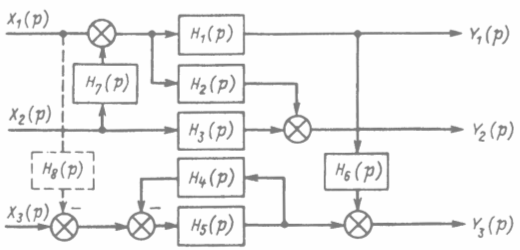
Составить структурную схему системы.
Дано:
![]() ;
;
![]() ;
;
![]() .
.
Рассматриваем линейную систему с постоянными параметрами:
![]() ,
,
![]() .
.
Преобразуем по Лапласу матричные уравнения:
![]() ; (1)
; (1)
![]() , (2)
, (2)
где
![]() ;
; ![]() ;
; ![]()
– лапласовы преобразования координат состояния ![]() , выходных
, выходных ![]() и входных
и входных ![]() сигналов.
сигналов.
Преобразуем уравнение (1):
![]()
Выносим за скобки:
![]()
где
![]() – единичная матрица.
– единичная матрица.
Умножаем слева на обратную матрицу:
![]()
Откуда получаем:
![]() .
.
Подставляем в уравнение (2):
![]()
Получаем:
![]()
Выражение ![]() называют передаточной функцией системы.
называют передаточной функцией системы.
Находим её:
![]()
Находим обратную матрицу:
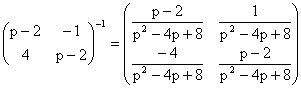
Подставляем:
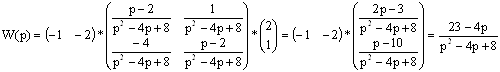 .
.
Для получения частотной передаточной функции производим замену в передаточной функции ![]() :
:
![]() ,
,
получаем:
 .
.
Выделим действительную и мнимую части:
![]() ,
,
для этого умножим числитель и знаменатель ![]() на комплексно – сопряжённый знаменатель:
на комплексно – сопряжённый знаменатель:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Годограф – это график частотной передаточной функции ![]() на комплексной плоскости при изменении частоты
на комплексной плоскости при изменении частоты ![]() от нуля до бесконечности.
от нуля до бесконечности.
Изменяя частоту, производим расчёт действительной ![]() и мнимой
и мнимой ![]() частей частотной передаточной функции.
частей частотной передаточной функции.
Результат расчёта записываем в таблицу 1.
Таблица 1. Расчёт годографа
|
|
|
|
|
|
|
|
|
|
| 0 | 2,8750000 | 0,0000000 | 10 | -0,0512719 | 0,4570747 | 200 | -0,00018 | 0,020008 |
| 1 | 2,7230769 | 0,9846154 | 20 | -0,0163435 | 0,2074170 | 300 | -0,000078 | 0,013336 |
| 2 | 1,9500000 | 1,9000000 | 30 | -0,0075500 | 0,1355448 | 400 | -0,000044 | 0,010001 |
| 3 | 0,8344828 | 1,9862069 | 40 | -0,0043030 | 0,1009350 | 500 | -0,000028 | 0,008001 |
| 4 | 0,2250000 | 1,5500000 | 50 | -0,0027705 | 0,0804792 | 600 | -0,000019 | 0,006667 |
| 5 | 0,0130624 | 1,1611030 | 60 | -0,0019302 | 0,0669441 | 700 | -0,000014 | 0,005715 |
| 6 | -0,0500000 | 0,9000000 | 70 | -0,0014209 | 0,0573176 | 800 | -0,000019 | 0,005000 |
| 7 | -0,0645030 | 0,7269777 | 80 | -0,0010893 | 0,0501171 | 900 | -0,000009 | 0,004445 |
| 8 | -0,0634615 | 0,6076923 | 90 | -0,0008614 | 0,0445267 | 1000 | -0,000007 | 0,004000 |
| 9 | -0,0578113 | 0,5216604 | 100 | -0,0006982 | 0,0400600 | 2000 | -0,000002 | 0,002000 |
Можно построить график на комплексной плоскости – рис. 1.
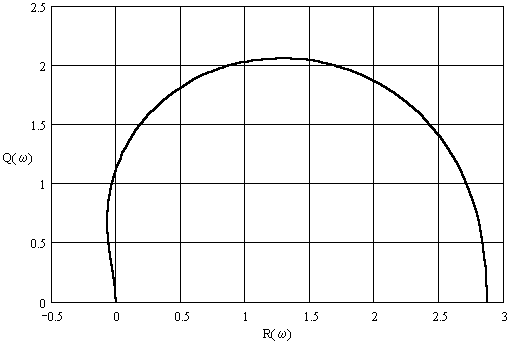
Рис. 1. Годограф
Импульсная характеристика вычисляется как обратное преобразование Лапласа от передаточной функции:
 .
.
Найдём полюса передаточной функции:
![]()
![]()
Видим – полюса расположены в правой полуплоскости, а это значит, что процесс будет расходящимся.
Разложим передаточную функцию на простые дроби:
![]() .
.
Используя табличные значения, находим:
![]() ,
,
![]() .
.
Таким образом, получаем:
![]() .
.
Изменяя время от нуля до 5 секунд, производим расчёт по формуле, результаты заносим в таблицу 2.
Таблица 2. Импульсная характеристика
|
| 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 |
|
| -4 | 11,28 | 62,69 | 100,8 | -167,1 | -1236 | -2395 | 2097 | 23854 | 54578 | -15944 |
Строим график импульсной характеристики – рис. 2.
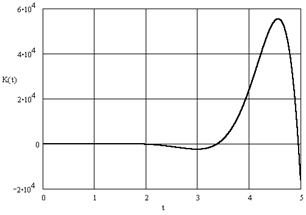
Рис. 2. Импульсная характеристика
Похожие работы
... имеют некоторый типовой вид. Сложные (многосвязные) технические объекты в совокупности с узлами (устройствами) управления первого, исполнительного уровня образуют подсистемы оперативного управления, которые представляют собой многосвязные системы автоматического регулирования (МСАР) по типу следящих систем. Задающие воздействия для них формируются на втором, тактическом уровне, а цели управления ...
... kL>kN, где через kL, kG, kN обозначены порядки старших производных полиномов от р в соответствующих матрицах L(p), G(p) и N(p). Уравнение движения САУ составляется на основе ее структуры и математического описания, входящих в систему элементов, и имеет вид уравнения (1.1.1), где u(t)=z(t) и z(t) - вектор задающих воздействий на систему. Уравнение движения САУ (1.1.1), записанное относительно ...
... по соответствующему полю). В окне Конструктора таблиц созданные связи отображаются визуально, их легко изменить, установить новые, удалить (клавиша Del). 1 Многозвенные информационные системы. Модель распределённого приложения БД называется многозвенной и её наиболее простой вариант – трёхзвенное распределённое приложение. Тремя частями такого приложения являются: ...
... , а 3 формируется путем умножения построчно колонок 1 и 2. Модель в абсолютных единицах после определения коэффициентов записывается в виде Динамическая идентификация Многие технологические объекты управления, функционирование которых в динамике еще недостаточно изучено, не могут быть описаны аналитически. Для получения их динамических моделей также применяются экспериментальные методы. ...

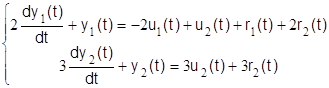
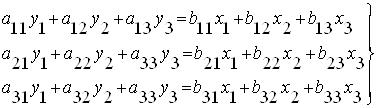
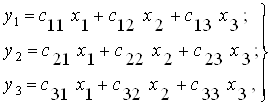
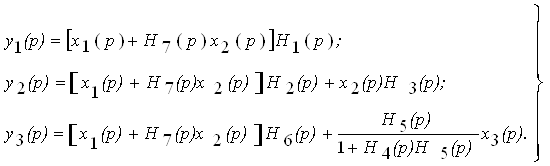
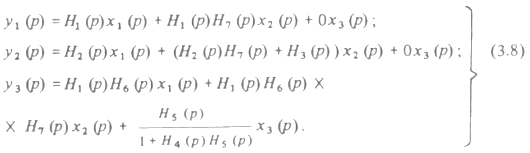
0 комментариев