Навигация
3.2. Проведение игры.
- Итак, начинаем игру. Сейчас мы будем работать с вами по 1 таблице
Таблица №1
| 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
-Итак, сверху вы видите номера ответов, а под ними соответствующие ответы. Я задаю вопрос, вы 5 секунд, думаете и поднимаете таблички с правильными ответами.
1. Какой вид имеет квадратное уравнение.
2. Назовите формулы корней квадратного уравнения.
3. Назовите неполное квадратное уравнение.
4. Назовите, чему равен дискриминант квадратного уравнения.
-Хорошо с этим заданием вы справились хорошо, почти все учащиеся поднимали таблички с правильными ответами. А кто ошибался, он еще раз увидел правильные формулы и надеюсь, так же доучит материал.
-А теперь мы все переходим во второй тур. Во втором туре мы выясним знание правил по данной теме. Работать будем со второй таблицей.
Таблица №2
| 1 | 2 | 3 | 4 | 5 |
| Теорема обратная теореме Виета | Квадратное уравнение | Теорема Виета | Неполное квадратное уравнение | Приводимое квадратное уравнение |
-Я буду говорить вам правило, а вы поднимайте соответствующую карточку.
1) Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
-Верно, следующий вопрос, слушайте и поднимайте таблички.
1) Если в квадратном уравнении ![]() хотя бы один из коэффициентов в или с равен нулю, то такое уравнение называется….
хотя бы один из коэффициентов в или с равен нулю, то такое уравнение называется….
-Верно, приведите пример квадратного уравнения.
2) Уравнение вида ![]() , где х переменная, а, в, с – некоторые числа, причем а ¹ 0 называется….
, где х переменная, а, в, с – некоторые числа, причем а ¹ 0 называется….
-Верно, приведите пример квадратного уравнения
Следующий вопрос
3) Если числа м и n таковы, что их сумма равна р, а произведение q, то эти числа являются корнями уравнения вида ![]()
-Верно, скажите, сколько корней имеет неполное квадратное уравнение каждого вида.
-Верно.
4) Как называются полные квадратные уравнения, у которых все три коэффициента отличны от нуля и в которых первый коэффициент равен 1.
-Хорошо и с этим заданием вы справились.
4. Самостоятельная работа. (Третий тур).
-Вам в этом туре необходимо выполнить следующие задания. На доске выписаны квадратные уравнения.
1. х2 – 15х – 16 = 0.
2. х2 – 9х + 20 = 0.
3. 2х2 + 2х – 112 = 0.
4. х2 – 6х + 8 = 0.
-Вы самостоятельно решаете эти уравнения в тетради, а потом мы проверим.
-Итак, я буду называть вам уравнения, а вы поднимайте карточку, соответствующую правильному ответу.
-Хорошо давайте проверим.
-Поднимите карточку, соответствующую правильному ответу для уравнения 2х2 + 2х – 112 = 0.
-А теперь составьте три неполных квадратных уравнения и решите их.
-Давайте посмотрим, какие уравнения вы составили
5. Подведение итогов
-Итак, вот и подходит к концу наша игра. В ходе игры мы повторили теоретический и практический материал, и теперь мы можем подвести урок игры. Подсчитайте свои звездочки
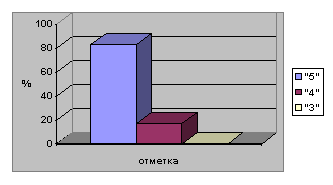
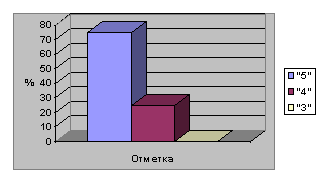
-Кто набрал от 20 до 25 звезд получают «5»
-Кто набрал от 20 до 15 звезд получают «4»
-Кто набрал 15 звезд и меньше получают «3»
Заключение
Автором была выполнена курсовая работа по теме «Формирование умения решения квадратных уравнений в 8-ом классе». При выполнении данной работы понадобились не только те знания, которые имеются у самого автора, но и необходимая работа с дополнительной литературой, составление конспектов уроков.
Благодаря выполнению этой работы можно сказать, что материал, связанный с уравнениями, составляет значительную часть школьного курса математики. На изучение темы «Квадратные уравнения» по программе дается всего 22 ч. Их изучение в современной методике математики связано с тремя главными областями своего возникновения и функционирования: прикладная направленность, теоретико-математическая направленность и направленность на установление связей с остальным содержанием курса математики.
Для этой темы характерна большая глубина изложения и богатство устанавливаемых с ее помощью связей в обучении, логическая обоснованность изложения. Поэтому она занимает исключительное положение в линии уравнений и неравенств. К изучению темы «Квадратные уравнения» учащиеся приступают, уже накопив определенный опыт, владея достаточно большим запасом алгебраических и общематематических представлений, понятий, умений. владение содержанием линии уравнений позволяет расширить список выполнимых преобразований. Так, умение решать квадратные уравнения позволяет осуществлять сокращение дробей, в числителе или знаменателе которых имеется квадратный трехчлен. В итоге изучения материала линии уравнений учащиеся должны не только овладеть применением алгоритмических предписаний к решению конкретных заданий, но и научиться использовать логические средства для обоснования решений в случаях, когда это необходимо.
Список литературы
1) Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. – 2-е изд. – М.: Просвещение, 2003. – 287 с.
2) Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров и др. – 10-е изд. – М.: Просвещение, 2003. – 255с.
3) Башмаков М.И. Алгебра: учеб. для 8 кл. общеобразоват. учреждений. – М.: Просвещение, 2004. – 287с.
4) Бекаревич А.Б. Уравнения в школьном курсе математики. – М., 1968.– 196 с.
5) Бурмистрова Т.А. Программы общеобразовательных учреждений // Математика.- М.: Просвещение,1994.
6) Глейзер Г.И. История математики в школе VII – VIII классы. – М., 1982.
7) Колягин Ю.М. Методика преподавания математике в средней школе. Частные методики. – М.: Просвещение, 1977.
8) Лягущенко Е.И. Методика обучения математике в 5 кл. – Минск, 1976.
9) Маркушевич Л.А., Черкасов Р.С. Уравнения и неравенства в заключительном повторении курса алгебры средней школы // Математика в школе. – 1994. - №1. – с.
10) Методика и технология обучения математике. Курс лекций: пособие для вузов / под ред. Н.Л.Стефановой, Н.С. Подходовой. – М.: Дрофа, 2005. – 416 с.
11) Мишин В.И. Методика преподавания математики в средней школе. – М.,1990.
12) Оганесян В.А. Методика преподавания математики в средней школе. – М.: Просвещение, 1980. – 368 с.
13) Панкратова Л. Обобщающий урок по теме «Квадратные уравнения» в форме игры «Звездный час» // Математика.-2002.-№21.
14) Сабинина Л.В. Методика в понятиях и терминах. Ч.1. – М.: Просвещение, 1978. – 320 с.
15) Столяр А.А. Общая методика преподавания математики. – М., 1985.
16) Шаталова С. Урок – практикум по теме «Квадратные уравнения».- 2004. -№42
Похожие работы
... список или выбрать из 2-3 текстов наиболее интересные места. Таким образом, мы рассмотрели общие положения по созданию и проведению элективных курсов, которые будут учтены при разработке элективного курса по алгебре для 9 класса «Квадратные уравнения и неравенства с параметром». Глава II. Методика проведения элективного курса «Квадратные уравнения и неравенства с параметром» 1.1. Общие ...
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
... и практическое использование различных форм уроков математики Для того чтобы доказать или опровергнуть, что использование различных форм уроков способствует улучшению качества знаний школьников по теме "Квадратные уравнения", были разработаны и проведены разнообразные формы уроков в 8 классе МОУ “Иштеряковская средняя общеобразовательная школа". При изучении темы были выбраны такие формы ...
... на качественно новую ступень овладения содержанием школьной математики. Глава II. Методико - педагогические основы использования самостоятельной работы, как средство обучения решению уравнений в 5 - 9 классах. § 1. Организация самостоятельной работы при обучения решению уравнений в 5 - 9 классах. При традиционном способе преподавания учитель часто ставит ученика в положение объекта ...
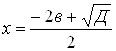
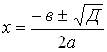
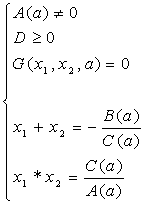






0 комментариев