Навигация
Найдем значение коэффициента корреляции
13837
знаков
21
таблица
25
изображений
3. Найдем значение коэффициента корреляции
Отсюда можно сделать вывод что зависимость прямая умеренная.
61-70. Найти выборочное уравнение прямой регрессии У на Х по данной корреляционной таблице.
61.
| Y | X | |||||||
| 4 | 9 | 14 | 19 | 24 | 29 |
| ||
| 10 | 2 | 3 | __ | __ | __ | __ | 5 | |
| 20 | __ | 7 | 3 | __ | __ | __ | 10 | |
| 30 | __ | __ | 2 | 50 | 2 | __ | 54 | |
| 40 | __ | __ | 1 | 10 | 6 | __ | 17 | |
| 50 | __ | __ | __ | 4 | 7 | 3 | 14 | |
|
| 2 | 10 | 6 | 64 | 15 | 3 | n=100 | |
Выберем в качестве ложных нулей варианты по х и у с наибольшими частотами.
Перейдем к условным вариантам
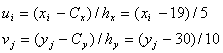
Получим таблицу в условных вариантах.
| V | U | |||||||
| -3 | -2 | -1 | 0 | 1 | 2 |
| ||
| -2 | 2 | 3 | __ | __ | __ | __ | 5 | |
| -1 | __ | 7 | 3 | __ | __ | __ | 10 | |
| 0 | __ | __ | 2 | 50 | 2 | __ | 54 | |
| 1 | __ | __ | 1 | 10 | 6 | __ | 17 | |
| 2 | __ | __ | __ | 4 | 7 | 3 | 14 | |
|
| 2 | 10 | 6 | 64 | 15 | 3 | n=100 | |
Найдем выборочные средние 
Найдем вспомогательные величины
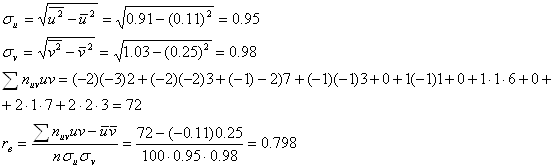
Перейдем теперь к исходным вариантам и составим уравнение регрессии
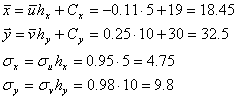
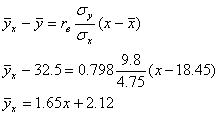
65.
| Y | X | |||||||
| 10 | 15 | 20 | 25 | 30 | 35 |
| ||
| 6 | 4 | 2 | __ | __ | __ | __ | 6 | |
| 12 | __ | 6 | 2 | __ | __ | __ | 8 | |
| 18 | __ | __ | 5 | 40 | 5 | __ | 50 | |
| 24 | __ | __ | 2 | 8 | 7 | __ | 17 | |
| 30 | __ | __ | __ | 4 | 7 | 8 | 19 | |
|
| 4 | 8 | 9 | 52 | 19 | 8 | n=100 | |
Выберем в качестве ложных нулей варианты по х и у с наибольшими частотами.
Перейдем к условным вариантам
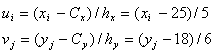
Получим таблицу в условных вариантах.
| V | U | |||||||
| -3 | -2 | -1 | 0 | 1 | 2 |
| ||
| -2 | 4 | 2 | __ | __ | __ | __ | 6 | |
| -1 | __ | 6 | 2 | __ | __ | __ | 8 | |
| 0 | __ | __ | 5 | 40 | 5 | __ | 50 | |
| 1 | __ | __ | 2 | 8 | 7 | __ | 17 | |
| 2 | __ | __ | __ | 4 | 7 | 8 | 19 | |
|
| 4 | 8 | 9 | 52 | 19 | 8 | n=100 | |
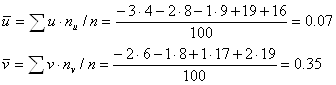Найдем выборочные средние Найдем вспомогательные величины
Вычислим коэффициент корреляции
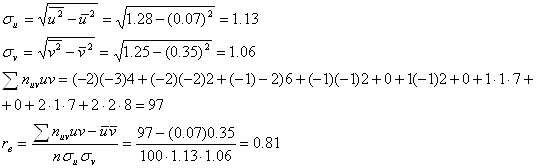
Перейдем теперь к исходным вариантам и составим уравнение регрессии
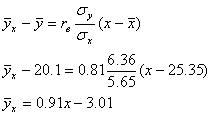
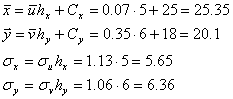
Уравнение регрессии
Похожие работы
... случайной величиной и все статистические выводы приходится делать, опираясь только на результаты «пробных» испытаний. Именно такие модели в основном рассматриваются в математической статистике. В математической статистике употребляют также понятие параметрической и непараметрической модели. Параметрическая модель возникает тогда, когда нам известен вид функции распределения наблюдаемого признака, ...
... Вариационные ряды позволяют получить первое представление об изучаемом распределении. Далее необходимо исследовать числовые характеристики распределения (аналогичные характеристикам распределения теории вероятностей): характеристики положения (средняя арифметическая, мода, медиана); характеристики рассеяния (дисперсия, среднее квадратическое отклонение, коэффициент вариации); характеристики ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... , вторая в среднем убывает. 3. D(x±h)=D(x)+D(h)±2mxh Доказательство. D(x±h)=M((x±h)2)—M2(x±h)=M(x2±2xh+h2)—(M(x)±M(h))2=M(x2)±2M(xh)+M(h2)—+M2(x)+2M(x)*M(h)—M2(h)=D(x)+D(h)±2(M(xh))—M(x)*M(h)=D(x)+D(h)±2mxh Вопрос 31 Мат. статистика опирается на теорию вероятностей, и ее цель – оценить характеристики генеральной совокупности по выборочным данным. Генеральной совокупностью называется ...
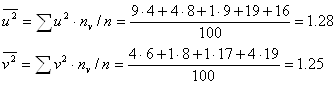
0 комментариев