Навигация
2. k = k+1
3. Вычисляем 
4. Ищем координату 
: 
5. Образуем вектор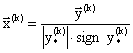 
6. Если 
, то собственным значением является 
;
= 
; в противном случае перейти к п. 2.
Существует модификация степенного метода, которая отличается от предыдущего алгоритма критерием остановки итерационного процесса.
Формульно-словесное описание метода:
1. Выбираем 
: 
, k=0, ε – точность вычисления максимального по модулю собственного значения, 
- некоторый допуск (близость к нулю компонент вектора );
2. k = k+1;
3. Вычисляем ;
4. Ищем координату : ;
5. Образуем вектор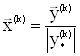 
;
6. Вычисляем 
для таких i, что 
, где - допуск;
7. Если 
, то собственным значением является 
, где j – число индексов, для которых выполняется условие ; в противном случае перейти к п. 2.
Основным достоинством степенного метода является то, что векторы получаются только с помощью умножения матрицы на вектор (плюс некоторая работа по вычислению нормирующих множителей); никаких преобразований самой матрицы 
при этом не требуется. Главный недостаток этого метода заключается в том, что он может сходиться очень медленно. Скорость сходимости в первую очередь определяется отношением 
. Если это отношение по модулю близко к 1, что характерно для многих практических задач, то сходимость будет медленной.
Степенной метод имеет и другие недостатки. Если имеется несколько собственных значений с максимальным модулем, например 
(а так всегда бывает в случае вещественной матрицы с доминирующей парой комплексно-сопряженных собственных значений), то итерационная последовательность (2) вообще не сходится.
Задание на лабораторную работу
Цель работы: изучение степенных методов расчета максимального по модулю собственного значения и соответствующего собственного вектора квадратной матрицы.
1. Ознакомиться со степенным методом вычисления максимального по модулю собственного значения матрицы A и его модификациями.
2. Составить и отладить программы, рассчитывающие максимальное по модулю собственное значение и соответствующий ему собственный вектор матрицы А произвольной.
3. Элементы матрицы А должны считываться из файла, точность расчета ε вводится с клавиатуры.
4. При проверке работоспособности программ для n=2 и n=3 выполнить ручной расчет собственных значений и собственных векторов матрицы А.
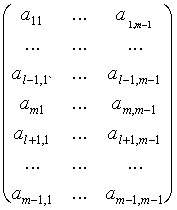
5. Нахождение собственных векторов и собственных значений следует провести, используя самостоятельно составленные и предложенные ниже тестовые примеры:
, 
,
.
6. При заданной точности расчета ε фиксировать выполненное число итераций k.
7. Составить отчет, который должен содержать следующие разделы:
- описание степенного метода и его модификаций
- описание исходных данных
- схемы-алгоритмов
- тексты программ;
- результаты расчетов тестовых примеров с использованием разработанных программ;
- анализ полученных результатов, выводы по работе;
- список литературы.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Вержбицкий В.М. Основы численных методов: Учебник для вузов. – М.: Высш. шк., 2002. – 840с.
2. Волков Е.А. Численные методы: Учебное пособие. – 3-е изд., испр. – СПб: Лань, 2004. – 248с.
3. Кетков Ю.Л. MATLAB 6: программирование численных методов. – СПб.: БВХ-Петербург, 2004. – 672с.
4. Турчак Л.И. Основы численных методов: Учебное пособие. – М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 320с.
Похожие работы
... на главной и двух побочных диагоналях, равны нулю при та В общем случае системы линейных алгебраических уравнений с трехдиагональной матрицей имеют вид Для численного решения систем трехдиагональными матрицами применяется метод прогонки, который представляет собой вариант метода последовательного исключения неизвестных. Т.е. матрицу А можно записать Идея метода прогонки состоит в ...
... D2 ∙ c = p. Отсюда получаем, что: c = D2 ∙ ( p - D1∙ u ) Таким образом, искомые константы найдены. Далее показано как применять этот метод для решения «жестких» краевых задач. Запишем V∙ K(1←0) ∙ ∙ = p. совместно с K(1←0) = K(1←x2) ∙ K(x2←x1) ∙ K(x1←0) и получим: V∙ K(1←x2) ∙ K(x2&# ...
... системы на ЭВМ, а так же требование его экономичности обуславливают применение регулярных сеток, расположение узлов в которых подчиняется определённым закономерностям. В практике численного моделирования микроэлектронных структур примеяются как непрерывные прямоугольные (неравномерные), так и треугольные сетки (рис.2.). Треугольная сетка позволяет с меньшим количеством дополнительных узлов сгущать ...
... Вывод Программа, разработанная в данной курсовой работе, реализует метод Зейделя для решения СЛАУ 6-го порядка. Она даёт гарантированно правильное решение системы линейных уравнений, если каждый элемент главной диагонали матрицы коэффициентов является единственным максимальным в своей строке, ненулевым, либо справедливы условия: максимальный элемент строки является единственным максимальным в ...
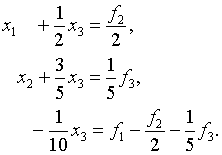
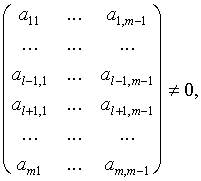
0 комментариев