Класс F равномерно ограничен, то есть существует L>0, такое, что f(t)£L при t³0, fÎF;

1. Класс F равномерно ограничен, то есть существует L>0, такое, что f(t)£L при t³0, fÎF;

2. ;

3. Множества I_k^- (k-1, U) – открыты для всех k>n+1;

4. Из любой последовательности {f_i}_i³1ÌI^-_k+1 (k>n) такой, что

,

можно выделить подпоследовательность, слабо относительно класса U сходящуюся к некоторой функции .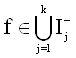

Пусть система  образует T₊ - систему на [0, ¥).

Рассмотрим систему функций , такую, что w_i=u_i для  и  - T₊ - системы для m³n (см. [1]).

Теорема 1. Пусть система  образует T₊ - систему на [0, ¥), F-нижний W-индексационный с дефектом n класс функций на [0, ¥). Тогда

.

Доказательство. Пусть . Согласно условию 2 определения индексационного класса, существует последовательность {f_j}_j³1ÌI_k^- такая, что . Зафиксируем произвольное f_l.

Если f_lÎI_k^-, где k£n+1, то положим f_l^*=f_l.

Пусть k>n+1 и s={} – (k-1, W) окрестность f_l в I_k^-.

Рассмотрим произвольные  и . Допустим, что . Согласно лемме 1, отношения и  невозможны для s£k-1. Следовательно,  и , что невозможно.

Таким образом, отображение  непрерывно и взаимно однозначно. Из принципа инвариативности области (см. [3]) следует, что  - открытое множество в R^k-1, содержащее .

Пусть ,  и  - многочлен по системе , имеющий k-2 нулей x₁, …, x_k-2. Условие b_k-1=0 противоречит чебышевости системы . Положим b_k-1>0. Тогда (см. [5]) P(t)>0 при t>x_k-2.

Имеем

,

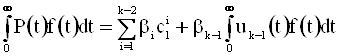где c_lⁱ – i-ая компонента вектора , и, следовательно,

.

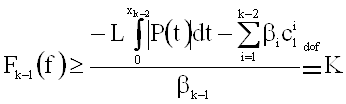Так как константа К не зависит от f, то m_l>-¥.

Кроме того, .

Возьмем последовательность , такую, что

F_k-1(f_lp)>F_k-1(f_lq)=m_l при p<q и

,

Рассмотрим произвольные f_lp и f_lq, где p<q. Так как , то отношения  и  невозможны для s£k-2. Отношения  и  невозможны, так как f_lp, f_lqÎI_k^-. Из леммы 1 получаем .

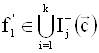Так как , то найдется функция , такая, что F_k-1(f_l^’)=m_l.

Отношение f_l^’ÎI_k^- невозможно, в силу определения числа m_l и принципа инвариативности области. Отношения f_l^’ÎI_m^- для m<k-1 невозможны, так как . Следовательно .

Продолжая таким образом, через k-n-2 шагов получим функцию , такую, что . Из условия 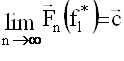 следует утверждение теоремы 1.

Замечание 1. Класс F непрерывных слева, неотрицательных функций на [0, ¥) назовем верхним U-индексационным с дефектом n, если: