Навигация
Класс F равномерно ограничен;
1. Класс F равномерно ограничен;
2.  ;
;
3. Множества Ik+ (k-1, U) – открыты для всех k>n+1;
4. Для k>n из любой последовательности {fi}i³1ÌIk+ такой, что
![]() ,
,
можно выделить подпоследовательность, относительно класса U слабо сходящуюся к некоторой функции 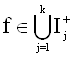 ;
;
5. Ik+ÌFU для k³n+1.
Теорема 2. Пусть система ![]() образует T+-систему на [0, ¥), F-верхний W-индексационный с дефектом n класс функций на [0, ¥). Тогда
образует T+-систему на [0, ¥), F-верхний W-индексационный с дефектом n класс функций на [0, ¥). Тогда
 .
.
Определение 6. Систему ![]() непрерывных на [0, ¥) функций назовем T+1-системой, если она является T+-системой, и, кроме того, системы u1, …, ul-1, ul+1, …, un также являются T+-системами для
непрерывных на [0, ¥) функций назовем T+1-системой, если она является T+-системой, и, кроме того, системы u1, …, ul-1, ul+1, …, un также являются T+-системами для ![]() .
.
Лемма 2. Пусть ![]() - T+1-система на [0, ¥), функции f и g таковы, что
- T+1-система на [0, ¥), функции f и g таковы, что
(-1)n-i Fi(f) ³ (-1)n-i Fi(g), ![]() .
.
Тогда отношения ![]() ,
, ![]() и
и ![]() ,
, ![]() , невозможны.
, невозможны.
Доказательство. Допустим, что имеет место отношение ![]() и 1£p£n.
и 1£p£n.
Пусть x1, …, xp-1 (-¥<x1<…<xp-1<¥) – точки перемен знака функции ![]() ; xо=-¥, xn=¥;
; xо=-¥, xn=¥; 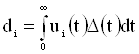 . Выберем точки xn-1<xn-2<…<xp<xp-1 так, чтобы
. Выберем точки xn-1<xn-2<…<xp<xp-1 так, чтобы ![]() ,
, ![]() ,
, ![]() . Рассмотрим систему равенств
. Рассмотрим систему равенств
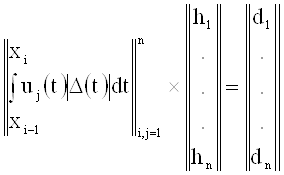 , (4)
, (4)
где hi=±1. Из условия ![]() следует, что hn=1. С другой стороны, из (4) получаем
следует, что hn=1. С другой стороны, из (4) получаем
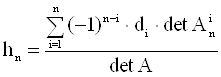 ,
,
где А – матрица, записанная в (4) слева, Ani – матрица, получаемая из А удалением i-ой строки и n-го столбца. Так как ![]() - T+1-система на [0, ¥), то detA>0, detAni>0,
- T+1-система на [0, ¥), то detA>0, detAni>0, ![]() . Следовательно, hn£0. Получили противоречие.
. Следовательно, hn£0. Получили противоречие.
Случай ![]() ,
, ![]() , рассматривается аналогично.
, рассматривается аналогично.
Теорема 3. Пусть ![]() - T+1-система на [0, ¥), F-нижний W-индексационный с дефектом n класс функций на [0, ¥). Тогда
- T+1-система на [0, ¥), F-нижний W-индексационный с дефектом n класс функций на [0, ¥). Тогда
![]() .
.
Доказательство. Пусть ![]() . Возьмем последовательность векторов
. Возьмем последовательность векторов ![]() так, чтобы
так, чтобы ![]() при
при ![]() и
и
![]()
для ![]() , j³1.
, j³1.
Согласно теореме 1, для любого ![]() найдется последовательность
найдется последовательность 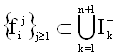 такая, что
такая, что ![]() .
.
Существует j1, такое, что ![]() , где r - какая-либо метрика в Rn, и
, где r - какая-либо метрика в Rn, и
![]() ,
, ![]() .
.
Выберем j2 так, чтобы ![]() и
и
![]() ,
, ![]() .
.
Продолжая таким образом, получим последовательность ![]() такую, что
такую, что 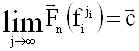 и
и
![]() (5)
(5)
Рассмотрим произвольные ![]() и
и ![]() . Отношения
. Отношения ![]() и
и ![]() для k>n невозможны, в силу условий
для k>n невозможны, в силу условий  .
.
Из неравенств (5), в силу леммы 2, имеем
![]() ,
,
т. е. существует функция 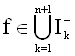 такая, что
такая, что ![]() . Включение
. Включение 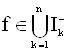 противоречит условию
противоречит условию ![]() , в силу принципа инвариативности области.
, в силу принципа инвариативности области.
Глава 1 Неравенство Маркова на индексационных классах
§ 1 Экстремальная задача
Пусть Â – некоторый класс функций распределения (ФР) на [a, b], -¥<a<b<¥; W(t) – (n+1) раз непрерывно дифференцируемая функция на [a, b], причем W(k)(t)>0 для tÎ[a, b] и ![]() ; c1, …, cn – вещественные константы; xÎ[a, b].
; c1, …, cn – вещественные константы; xÎ[a, b].
Экстремальная задача. Найти супремум и инфимум интеграла
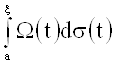
на множестве ![]()
![]() ФР из Â, удовлетворяющих ограничениям
ФР из Â, удовлетворяющих ограничениям
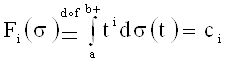 ,
, ![]() .
.
Для классов Âo - всех ФР на [a, b] и ВL – ФР на [a, b], удовлетворяющих условию 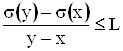 , -¥<x<y<¥, задача решена в [1].
, -¥<x<y<¥, задача решена в [1].
Важность решение экстремальных задач на разных классах ФР обоснована, например, в [1 - 5].
Задача при x=b решена в [4] для мажоризационных классов.
Анализ задачи на мажоризационных классах в общем случае наталкивается на трудности. Выход мы видим в рассмотрении классов с иной структурой – индексационных классов ФР.
Ниже предполагается, что Â - индексационный с дефектом n класс ФР на [a, b]. Определение индексационного с дефектом n класса приведено в [5]. Индексационными являются многие важные классы ФР, например, Âo, BL, класс унимодальных ФР на [a, b] и др.
Обозначим (k³1, AÌÂ, sÎÂ): Ik+ (Ik-) –множество всех ФР из Â, имеющих индекс k+ (k-); ![]() ;
; ![]() - пространство моментов порядка k;
- пространство моментов порядка k;  ;
; ![]() ;
; ![]() ,
, ![]() .
.
Основной результат работы содержится в утверждении.
Теорема. Пусть ![]() ,
, ![]() . Тогда:
. Тогда:
1. 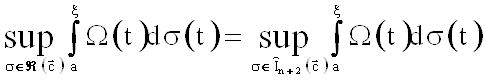 ,
,
2. 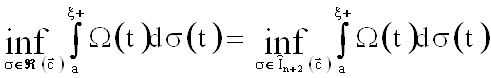
![]() ,
,
3. 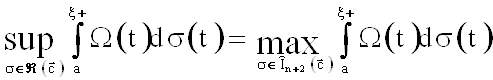 ,
,
4. 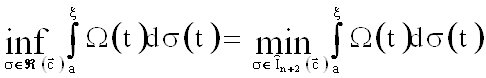 .
.
§ 2 Свойства отображения 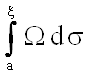
Нам понадобятся два факта из [6].
1. Для любого ![]() существует и единственная ФР
существует и единственная ФР ![]() .
.
2. Если ![]() , то множество
, то множество ![]() одноэлементно. Если
одноэлементно. Если ![]() , то существуют непрерывные, однопараметрические семейства
, то существуют непрерывные, однопараметрические семейства ![]() (т. е.
(т. е. ![]() при
при ![]() и
и ![]() (значок Þ обозначает слабую сходимость)) и
(значок Þ обозначает слабую сходимость)) и ![]() ФР такие, что
ФР такие, что ![]() ,
,![]() ,
, ![]() , для aÎ(0,1) и
, для aÎ(0,1) и ![]() для bÎ(0,1).
для bÎ(0,1).
Пусть ![]() и
и 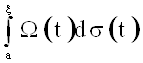 , где
, где ![]() , xÎ[a, b].
, xÎ[a, b].
Функция Ás непрерывна слева на [a, b] и Ás(a)=0 для всех sÎÂ. Так как W(t)>0 при tÎ[a, b], то Ás(x) не убывает по x.
Далее, из skÞs при k®¥ следует ![]() Á
Á![]() ÞÁs. Следовательно, семейства распределений {Á
ÞÁs. Следовательно, семейства распределений {Á![]() } и {Á
} и {Á![]() } непрерывны.
} непрерывны.
Определение 1. Функция f имеет на [a, b] m строгих перемен знака, если существуют множества B0(f)<…<Bm(f) (под X<Y (X, YÌR1) понимаем x<y для всех xÎX, yÎY) из [a, b] такие, что (-1)jf(x)>0 (или (-1)j+1f(x)>0 при xÎBj(f), ![]() и f(x)=0 при
и f(x)=0 при 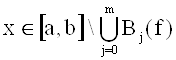 .
.
Лемма 1. Для любого распределения Á![]() (Á
(Á![]() ) и для любого Ám,
) и для любого Ám, ![]() , функция Ám - Á
, функция Ám - Á![]() (Ám - Á
(Ám - Á![]() ) имеет либо n+1, либо n+2 строгих перемен знака на [a, b].
) имеет либо n+1, либо n+2 строгих перемен знака на [a, b].
Доказательство. Предположим, что функция Ám - Á![]() имеет более n+2 строгих перемен знака. Тогда существуют a<x0<x1<…<xn+3£b такие, что (-1)i [Ám
имеет более n+2 строгих перемен знака. Тогда существуют a<x0<x1<…<xn+3£b такие, что (-1)i [Ám![]() -Á
-Á![]() ] > 0,
] > 0, ![]() . Кроме того, Ám(a)=Á
. Кроме того, Ám(a)=Á![]() (a)=0. Следовательно, существуют точки y0Î[a, x0), y1Î[x0, x1), …, yn+3Î[xn+2, xn+3) такие, что функция (-1)i[m(t) - ha(t)] возрастает в точке yi,
(a)=0. Следовательно, существуют точки y0Î[a, x0), y1Î[x0, x1), …, yn+3Î[xn+2, xn+3) такие, что функция (-1)i[m(t) - ha(t)] возрастает в точке yi, ![]() , что противоречит условию
, что противоречит условию ![]() .
.
Равенство ![]() запишем в виде
запишем в виде
 Ás(t)=ci,
Ás(t)=ci, ![]() ,
,
где 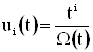 ,
, ![]() , с0 = 1.
, с0 = 1.
Очевидно, что последовательности u0, …, uk, ![]() , образуют T+ - системы на [a, b]. Из условия W(k)(t)>0 для tÎ[a, b] и
, образуют T+ - системы на [a, b]. Из условия W(k)(t)>0 для tÎ[a, b] и ![]() следует (см. [1]), что последовательности –u0, …,-uk
следует (см. [1]), что последовательности –u0, …,-uk![]() , также образуют T+ - системы. Следовательно, выполнены условия мажоризационной теоремы (см. [4]) и функция Ám - Á
, также образуют T+ - системы. Следовательно, выполнены условия мажоризационной теоремы (см. [4]) и функция Ám - Á![]() не может иметь n+1 строгих перемен знака.
не может иметь n+1 строгих перемен знака.
Пусть функция f(t) имеет k строгих перемен знака на [a, b]. Наряду с множествами Bi(f) строгого знакопостоянства рассмотрим множества P0(f)=(-¥, infB1(f)], Pi(f)=[supBi-1(f), infBi+1(f)],
![]() , Pk(f)=[supBk-1(f), +¥).
, Pk(f)=[supBk-1(f), +¥).
Зафиксируем ФР ![]() . Рассмотрим два класса функций
. Рассмотрим два класса функций
{Da=Ás - Á![]() :aÎ[0,1]} и {db=Ás - Á
:aÎ[0,1]} и {db=Ás - Á![]() :bÎ[0,1]}.
:bÎ[0,1]}.
Число a (число b) назовем: параметром первого типа, если функция Da (db) имеет n+2 строгих перемен знака (в этом случае на последнем множестве строго знакопостоянства функция Da (db) отрицательна (положительна)); параметром второго типа, если функция Da (db) имеет n+1 строгих перемен знака, причем на последнем множестве строгого знакопостоянства она отрицательна; параметром третьего типа, если функция Da (db) имеет n+1 перемен знака, причем на последнем множестве строгого знакопостоянства она положительна.
Каждому aÎ[0,1] (bÎ[0,1]) сопоставим набор из n+3 множеств X0(a), …, Xn+2(a) (Y0(b), …, Yn+2(b)) следующим образом. Если a (b) есть:
1.параметр первого типа, то
Xi(a)=Pi(Da), ![]() (Yi(b)=Pi(db),
(Yi(b)=Pi(db), ![]() );
);
2.
3.параметр второго типа, то
Xi(a)=Pi-1(Da), ![]() , X0(a)=(-¥, infB0(Da)],
, X0(a)=(-¥, infB0(Da)],
(Yi(b)=Pi(db), ![]() , Yn+2(b)=(supBn+1(db), +¥));
, Yn+2(b)=(supBn+1(db), +¥));
4.параметр третьего типа, то
Xi(a)=Pi(Da), ![]() , Xn+2(a)=[supBn+1(Da), +¥)),
, Xn+2(a)=[supBn+1(Da), +¥)),
(Yi(b)=Pi-1(db), ![]() , Y0(b)=(-¥, infB0(db)]).
, Y0(b)=(-¥, infB0(db)]).
Таким образом:
(-1)n-iDa(t)£0 при tÎIntXi(a), ![]() , (1)
, (1)
(-1)n-idb(t)³0 при tÎIntYi(b), ![]() .
.
При этом ни для какого i не существует интервала X, для которого выполнено строгое включение XÉIntXi(a) и (-1)n-iDa(t)£0 при tÎX. Ни для какого i не существует интервала YÉIntYi(b) и (-1)n-idb(t)³0 при tÎY.
Заметим также, что Xi(0)=Yi+1(0), Xi+1(1)=Yi(1).
Определение 2. Отображение Z(g): gÎ[0, 1]®Z(g)ÌR1 непрерывно, если из gi®g0, xi®x0, где g0, gi Î[0, 1], xiÎZ(gi), i³1, следует x0ÎZ(g0).
Лемма 2. Отображения Xi(a), Yi(b), ![]() непрерывны.
непрерывны.
Доказательство. Пусть aj®a, j®¥. Обозначим через ![]() границы отрезка Xi(aj). Определим a0=-¥. Возьмем произвольную точку a1 сгущения последовательности {a1(j)}j³1. Пусть для удобства
границы отрезка Xi(aj). Определим a0=-¥. Возьмем произвольную точку a1 сгущения последовательности {a1(j)}j³1. Пусть для удобства ![]() . Проделаем ту же операцию с последовательностями {ai(j)}j³1,
. Проделаем ту же операцию с последовательностями {ai(j)}j³1, ![]() и {bi(j)}j³1,
и {bi(j)}j³1, ![]() . Положим bn+2=+¥.
. Положим bn+2=+¥.
Итак,
![]() ,
, ![]() ,
, ![]() (2)
(2)
причем -¥=a0<a1£b0£a2£b1£…£an+1£bn£an+2£bn+1<bn+2=+¥.
Из (1) и (2) следует, что для(-1)n-iDa(t)£0 (3)
при tÎ(ai, bi), если ai¹bi.
Из (3) и 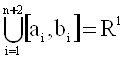 следует, что ai¹bi,
следует, что ai¹bi, ![]() , так как в противном случае функция Da имело бы не более n строгих перемен знака, что противоречит лемме 1. Отсюда и из определения Xi(a) следует [ai, bi]ÌXi(a),
, так как в противном случае функция Da имело бы не более n строгих перемен знака, что противоречит лемме 1. Отсюда и из определения Xi(a) следует [ai, bi]ÌXi(a),![]() . Для любого i из xjÎ[ai(j), bi(j)] и xj®x0 вытекает, что x0Î[ai, bi]. Следовательно, x0ÎXi(a).
. Для любого i из xjÎ[ai(j), bi(j)] и xj®x0 вытекает, что x0Î[ai, bi]. Следовательно, x0ÎXi(a).
Непрерывность отображений Yi(b) доказывается аналогично.
§ 3 Доказательство теоремы
В случае ![]() утверждение теоремы очевидно.
утверждение теоремы очевидно.
Пусть ![]() .
.
Лемма 3. Для любого ФР ![]() и любой точки xÎ[a, b] существует ФР
и любой точки xÎ[a, b] существует ФР ![]() такая, что Áv(t)³Ás(t) (Áv(t)£Ás(t)) в некоторой окрестности точки x.
такая, что Áv(t)³Ás(t) (Áv(t)£Ás(t)) в некоторой окрестности точки x.
Доказательство. Если не существует такого i, 0£i£n+2, что n-1 четно и xÎYi(0), то в некоторой окрестности точки x имеет место d0£0. В этом случае положим ![]() .
.
Пусть существует i такое, что n-i четно и xÎYi(0).
Случай I, i¹n+2. a) Предположим, что xÏYi(1). Пусть ![]() . Согласно лемме 2, xÎYi(b¢). В силу сделанного предположения, b¢<1 и, следовательно, существует последовательность {bj}j³1 такая, что xÎYi(bj) и bj®b¢. Пусть для некоторого bl не существует такого k, что n-k четно и xÎYk(bl). Тогда
. Согласно лемме 2, xÎYi(b¢). В силу сделанного предположения, b¢<1 и, следовательно, существует последовательность {bj}j³1 такая, что xÎYi(bj) и bj®b¢. Пусть для некоторого bl не существует такого k, что n-k четно и xÎYk(bl). Тогда ![]() в некоторой окрестности точки x. В этом случае полагаем
в некоторой окрестности точки x. В этом случае полагаем ![]() . Если же для всех bj, j³1, существует kj такие, что n-kj четны и
. Если же для всех bj, j³1, существует kj такие, что n-kj четны и ![]() , то существует m, m¹i, такое, что n-m четно и xÎYm(bj) для бесконечного числа элементов последовательности {bj}. По лемме 2 xÎYm(b¢). Так как n-i и n-m четны, то m¹i-1, m¹i+1. Вместе с m¹i это противоречит включению xÎYi(b¢).
, то существует m, m¹i, такое, что n-m четно и xÎYm(bj) для бесконечного числа элементов последовательности {bj}. По лемме 2 xÎYm(b¢). Так как n-i и n-m четны, то m¹i-1, m¹i+1. Вместе с m¹i это противоречит включению xÎYi(b¢).
б) Предположим, что xÎYi(1)=Xi+1(1). Пусть a¢=inf{a:xÎXi+1(a)}. Согласно лемме 2, xÎXi+1(a¢). Если a¢=0, то xÎXi+1(0)=Yi+2(0). Это противоречит условию xÎXi+1(a¢). Поэтому a¢¹0 и дальнейшее рассмотрение аналогично приведенному в а).
Случай II, i=n+2. а) При x¹Yn+2(1) доказательство аналогично доказательству пункта а) случая I.
б) Пусть xÎYn+2(1). Так как Yn+2(1)ÌYn+1(1), то xÎYn+1(1). Точка x не может совпадать с левым концом отрезка Yn+1(1), так как в этом случае множества Yn+1(1) и Yn+2(1) совпадают, что невозможно. Так как xÎYn+1(1) и не совпадает с левым концом отрезка Yn+1(1), то d1(t)£0 в некоторой окрестности точки x. В этом случае полагаем ![]() .
.
Итак, доказано существование такой ФР ![]() , что Ás-Án£0 в некоторой окрестности точки x. Случай Ás-Án³0 рассматривается аналогично.
, что Ás-Án£0 в некоторой окрестности точки x. Случай Ás-Án³0 рассматривается аналогично.
Теорема следует из леммы 3 и утверждения:
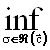 Ás(x) и
Ás(x) и 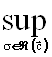 Ás(x+0) достижимы. Докажем последнее.
Ás(x+0) достижимы. Докажем последнее.
Пусть d=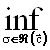 Ás(x) . Пусть последовательность ФР
Ás(x) . Пусть последовательность ФР ![]() , i³1, такова, что Á
, i³1, такова, что Á![]() . Выберем подпоследовательность последовательности {si}, слабо сходящуюся к некоторой ФР
. Выберем подпоследовательность последовательности {si}, слабо сходящуюся к некоторой ФР ![]() . Покажем, что Ás(x)=d. Для произвольного e>0 выберем x¢<x такое, что Ás(x)-Ás(x¢)<e¤2 и x¢- точка непрерывности Ás. Существует номер N такой, что для любого j>N выполнено неравенство ½Á
. Покажем, что Ás(x)=d. Для произвольного e>0 выберем x¢<x такое, что Ás(x)-Ás(x¢)<e¤2 и x¢- точка непрерывности Ás. Существует номер N такой, что для любого j>N выполнено неравенство ½Á![]() (x¢)-Ás(x¢)½<e¤2, из которого следует, что Ás(x¢) - Á
(x¢)-Ás(x¢)½<e¤2, из которого следует, что Ás(x¢) - Á![]() (x¢)<e, j>N. Так как Á
(x¢)<e, j>N. Так как Á![]() (x¢) £ Á
(x¢) £ Á![]() (x), то Ás(x) - Á
(x), то Ás(x) - Á![]() (x)<e, откуда следует Ás(x) - d£e. Последнее неравенство влечет Ás(x)=d.
(x)<e, откуда следует Ás(x) - d£e. Последнее неравенство влечет Ás(x)=d.
Глава 2 О чебышевской экстремальной задаче на [0, ¥)
В настоящей работе на конкретных классах функций распределения (ФР) даны два подхода к решению чебышевской экстремальной задачи на [0, ¥).
Чебышевская экстремальная задача. Пусть Â - выпуклый класс ФР на [0, ¥), системы u0º1 на [0, ¥) функций образуют T+-системы на [0, ¥).
Положим (1£i£n, sÎÂ):
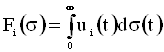 ,
, ![]() ,
,
![]() - моментное пространство класса Â относительно системы
- моментное пространство класса Â относительно системы ![]() .
.
Пусть ![]() .
.
Найти 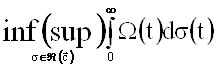 , где
, где ![]() .
.
10. Первый подход заключается в урезании справа класса  в точке x>0, наложении условий, при которых задача на «урезанном» классе Âх решается, и в переносе предельным переходом x®¥ решения на класс Â.
Для любого x>0 введем подкласс класса Â: Âх={sÎÂ:s(x+0)=1}.
Очевидно, для любых x1<x2
![]() (1)
(1)
Предположим, что для любого x>0 Âх - индексационный с дефектом n класс ФР на [0, x] ([5]).
Примерами таких классов служат: класс всех ФР на [0, ¥), класс ФР вогнутых на [0, ¥),класс ФР s на [0, ¥), удовлетворяющих при 0£x<y<¥ неравенству 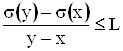 , L>0 и т. д.
, L>0 и т. д.
Перечисленные выше классы являются нижними индексационными ([2]), т. е. для них выполнено включение
 (
(![]() -замыкание множества XÌRn),
-замыкание множества XÌRn),
где Ii- - множество всех ФР, имеющих индекс i- в Â.
Кроме того, для этих классов справедливо включение ![]() , и следовательно,
, и следовательно,
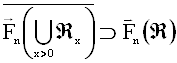 (2)
(2)
Лемма 1. ![]() .
.
Доказательство. Пусть ![]() . Из выпуклости множества
. Из выпуклости множества ![]() следует, что точка
следует, что точка ![]() является внутренней точкой некоторого (n+1)-мерного симплекса, лежащего в
является внутренней точкой некоторого (n+1)-мерного симплекса, лежащего в ![]() , т. е. существуют векторы
, т. е. существуют векторы ![]() , и числа l1>0, …, ln>0, ln+1>0 такие, что
, и числа l1>0, …, ln>0, ln+1>0 такие, что ![]() .
.
Из (2) следует существование последовательностей ![]() , таких, что
, таких, что
 .
.
Тогда для достаточно больших k выполнено равенство
![]() ,
,
где ![]() ,
, ![]() .
.
Следовательно, 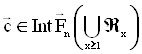 .
.
Из леммы 1 следует, что ![]() для достаточно больших x. Так как класс Âx является индексационным на [0, x], то ([5])
для достаточно больших x. Так как класс Âx является индексационным на [0, x], то ([5])
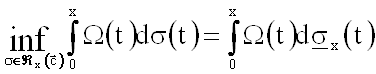 ,
,
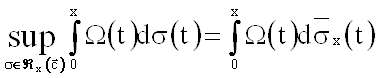 ,
,
где ![]() ,
, ![]() (
(![]() ) – ФР с нижним (верхним) индексом n+1 в классе Âx.
) – ФР с нижним (верхним) индексом n+1 в классе Âx.
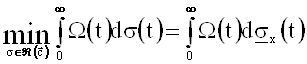 .
.
Из (1) следует, что
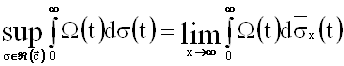 .
.
Вид экстремальных ФР ![]() и
и ![]() для рассматриваемых классов имеется в [5].
для рассматриваемых классов имеется в [5].
20. Второй подход продемонстрируем на примере класса Â0 всех ФР на [0, ¥).
Лемма 2. Если u0, u1, …, un – T+-система на [0, ¥), то для всех i и j существуют пределы 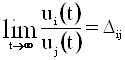 .
.
Доказательство. Из определения T+-системы следует, что для произвольных i, j и чисел a, b функции uj(t) и auj(t)+buj(t) обращаются в нуль более, чем в n+1 точках.
Пусть х – наибольшее решение уравнения uj(t)=0. Рассмотрим уравнение
auj(t)+buj(t)=0, t>x. (3)
Уравнение 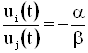 (ui(t)¹0, t>x) имеет не более (n+1) решений на (x, ¥) при любых a, b.
(ui(t)¹0, t>x) имеет не более (n+1) решений на (x, ¥) при любых a, b.
Пусть 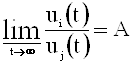 ,
, 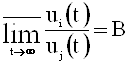 .
.
Допустим, что 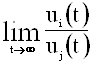 не существует, т. е. А<B.
не существует, т. е. А<B.
Введем последовательности {ti}i³1, {ti}i³1, удовлетворяющие условиям:
а) tk®¥, tk®¥ при k®¥;
б) 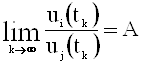 ,
, 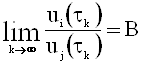 ;
;
в) t1<t1<t2<t2<…<tm<tm<… .
Пусть cÎ(A, B).
Из-за непрерывности функции ![]() на (x, ¥) уравнение
на (x, ¥) уравнение
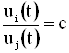
имеет бесконечное множество решений на (x, ¥).
Выберем 0£j0£n так, чтобы ![]() для всех
для всех ![]() и обозначим
и обозначим ![]() .
.
Пусть число t0 таково, что ![]() при t>t0.
при t>t0.
Рассмотрим функцию 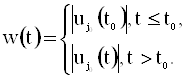
Пусть 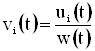 ,
, ![]() ,
, 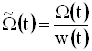 .
.
Легко видеть, что системы v0, v1, …, vn и v0, v1, …, vn, W являются T+-системами на [0, ¥).
Предположим, что эти системы являются T+-системами также на [0, ¥], т. е. для любых 0£t0<t1<…<tn-1<tn<¥
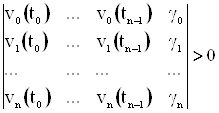 ,
,  ,
,
где 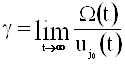 .
.
Через ![]() обозначим множество ФР sÎÂ0, для которых интегралы
обозначим множество ФР sÎÂ0, для которых интегралы 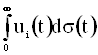 ,
, ![]() , абсолютно сходятся.
, абсолютно сходятся.
Пусть ![]() - моментное пространство класса
- моментное пространство класса ![]() относительно системы
относительно системы ![]() .
.
Рассмотрим класс непрерывных слева и неубывающих на [0, ¥) функций 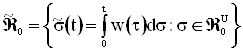 .
.
Имеем 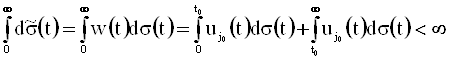 , т. е.
, т. е. 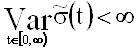 .
.
Заметим, что отображение ![]() является взаимно однозначным, причем
является взаимно однозначным, причем 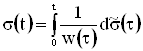 .
.
Таким образом, ![]() - множество всех неубывающих, непрерывных слева функций ограниченной вариации на [0, ¥).
- множество всех неубывающих, непрерывных слева функций ограниченной вариации на [0, ¥).
Пусть ![]() .
.
Необходимо найти
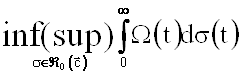 . (4)
. (4)
Из равенств (sÎÂ0U)
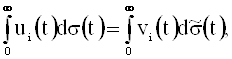
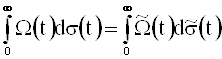
следует, что задача (4) эквивалентна следующей.
Найти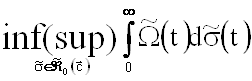 , (5)
, (5)
где ![]() - множество функций
- множество функций ![]() , удовлетворяющих равенствам
, удовлетворяющих равенствам
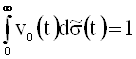 ,
, 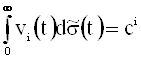 ,
, ![]() .
.
Таким образом, задача в классе Â0 сведена к задаче (5), решение которой приведено, например, в [3].
Именно для любого ![]()
![]()
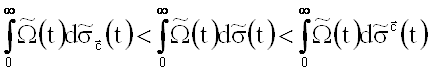 ,
,
где ![]() - ступенчатая функция, имеющая положительные скачки в точках
- ступенчатая функция, имеющая положительные скачки в точках ![]() при нечетном n и в точках
при нечетном n и в точках ![]() при четном n,
при четном n, ![]() - ступенчатая функция, имеющая положительные скачки в точках
- ступенчатая функция, имеющая положительные скачки в точках ![]() при нечетном n и в точках
при нечетном n и в точках ![]() при четном n.
при четном n.
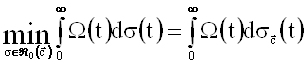 ,
,
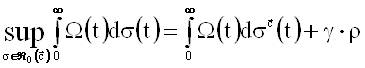 ,
,
где 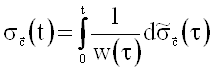 ,
, 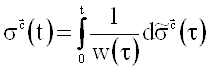 ,
,
r - величина скачка функции ![]() в точке ¥.
в точке ¥.
Литература
1. Крейн М.Г., Нудельман А.А. Проблема моментов Маркова и экстремальные задачи. – Москва: Наука, 1973.
2. Таталян К.Р. Экстремальные задачи проблемы моментов на классах распределений. – Дисс. на соиск. ученой степени кандидата физ.-мат. наук. Москва, МИЭМ, 1988.
3. Карлин С., Стадден В. Чебышевские системы и их применение в анализе и статистике. – Москва: Наука, 1976.
4. Даниэлян Э.А., Таталян К.Р. О проблеме моментов на мажоризируемых классах. – Ереван: Межвуз. сб. научн. трудов “Прикладная математика”, № 7, 1988.
5. Манукян В.Р. О проблеме моментов для индексационных классов распределений. – Ереван: ДАН РА, том XCI, № 4, 1990.
0 комментариев