Навигация
Построение прямой аппроксимирующей свойства тренда с помощью МНК
1. Построение прямой аппроксимирующей свойства тренда с помощью МНК
Наша ошибка сгенерирована по логнормальному закону с математическим ожиданием равным 0 и дисперсией равной 1. Гистограмма распределения шума представлена на рисунке 5.
![]()
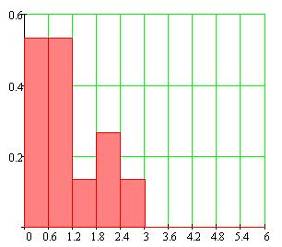
Рисунок 5. (Гистограмма распределения значений шума по интервалам).
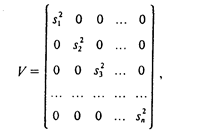
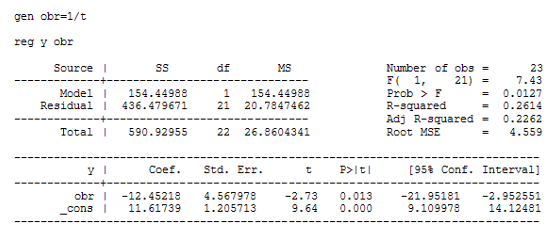
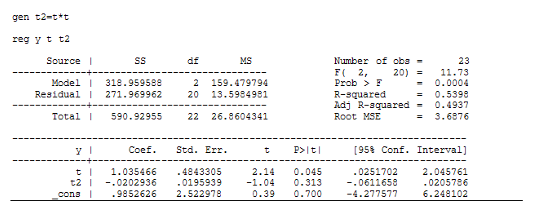
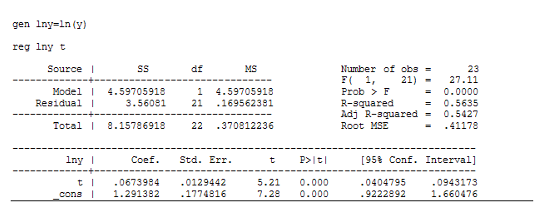
С помощью формул (21) и (22) вычислим коэффициенты линейного уравнения тренда с учетом шума с помощью метода МНК:
![]()
![]()
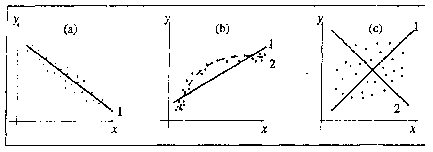
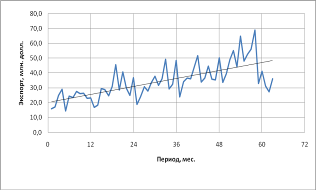
По найденным коэффициентам строим график прямой, которая аппроксимирует основные свойства линейного тренда. График показан на рисунке 6:
![]()
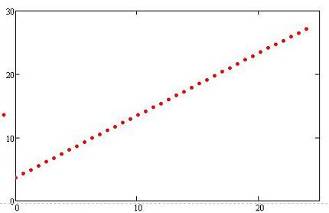
Рисунок 6. (Прямая, построенная по методу наименьших квадратов).
2. Прогнозирование дальнейшего продвижения тренда
Наша задача состоит в том, чтобы спрогнозировать дальнейшее поведение уравнения тренда и определить расхождения с спрогнозированными значениями.
Для этого увеличиваем участок наблюдения за линейным трендом без шума до τ =2t=50
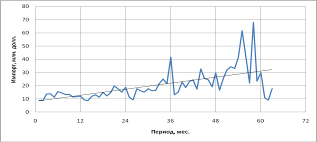
График расхождения исходного тренда и аппроксимированного тренда по МНК виден на рисунке 7. (Yτ – исходный тренд; Zτ – аппроксимированный тренд по МНК)
![]()
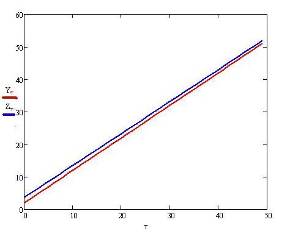
Рисунок 7 (На рисунке показаны тренд и аппроксимирующая его свойства прямая, построенная по методу наименьших квадратов).
Расхождения вычислены на удаленно отрезке(τ=50):
Δ= Zτ - Yτ =0.864
Проведем серию из 25 экспериментов по вычислению расхождений Δ по модулю:
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Δ | 0.661 | 0.673 | 0.756 | 2.366 | 0.488 | 3.569 | 0.864 | 5.651 | 2.328 | 0.851 | 1.259 | 1.718 | 0.618 |
| N | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
|
| Δ | 3.765 | 0.502 | 3.762 | 1.369 | 2.185 | 0.494 | 1.851 | 0.067 | 2.012 | 4.429 | 3.441 | 0.601 |
|
Рассчитаем среднее значение Δ и среднеквадратичное отклонение по формулам (6) и (8):
Δср=1.851; σ=1.484
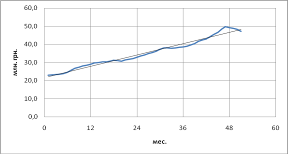
График на рисунке 8 отображает расхождения между исходной функцией и прямыми, полученными в результате аппроксимации по МНК. Синим цветом показаны полученные прямые, красным - исходная функция.
![]()
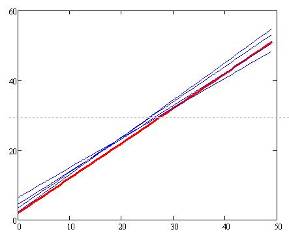
Рисунок 8. (На рисунке показаны тренд и несколько прямых, построенных по методу наименьших квадратов и аппроксимирующих свойства тренда).
Похожие работы
... рассчитать коэффициент парной регрессии, не решая системы уравнений. Ясно также, что если рассчитаны линейные регрессии х(у) и у(х), то произведение коэффициентов dx и by, равно r2: (7)[1] Взвешенный метод наименьших квадратов Далеко не все задачи исследования взаимосвязей экономических переменных описываются обычной линейной регрессионной моделью. Во-первых, исходные данные могут не ...
... Как видно из таблиц, обнаружилась автокорреляция только первого и второго порядков. Это говорит о том, что значительное влияние на урожайность озимой пшеницы в данном году оказывает урожайность двух предыдущих лет. 3. Метод экспоненциального сглаживания Выберем теперь форму зависимости (линейную или параболическую) методом экспоненциального сглаживания. Рассчитаем начальные условия ...
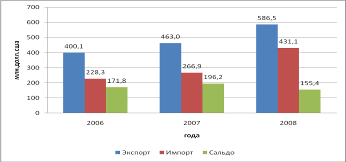
.1 Общая картина внешнеэкономической деятельность в Автономной Республике Крым в 2008 году По состоянию на 01.01.2009г. объёмы экспорта товаров в Автономной Республике Крым составили 586,5 млн.долл.США, импорта – 431,1 млн.долл.США. По сравнению с 2007 годом объёмы экспорта увеличились на 26,7%, импорта – в 1,6 раза. Положительное сальдо внешней торговли товарами составило 155,4 млн.долл. (в ...
... , проблема научного предусмотрения охватывает как теоретико-познавательный аспект, связанный с исследованием прогнозов как функции законов и теории наук, так и практический аспект, который выражается, в частности, в непосредственной связи прогнозирования с планированием и управлением.(11) 3.3 Классификация методов прогнозирования Методы прогнозирования можно разделить на две группы. Это ...

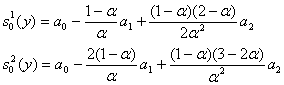


0 комментариев