Навигация
Проверка близости по критерию χ2 Пирсона закона распределения расхождений наблюдений и сгенерированного шума
4. Проверка близости по критерию χ2 Пирсона закона распределения расхождений наблюдений и сгенерированного шума
Проверим насколько расходятся значения при прогнозе и по тренду. Для этого определяются интервалы разбиения расхождений прогноза и вычисление вероятностей попасть в интервал по логнормальному закону с математическим ожиданием равным 0 и дисперсией 1 по формуле (9).
Далее посчитаем сумму квадратов расхождения между частотами и вероятностью попасть в интервал логнормального закона:
 (25)
(25)
На основе суммы квадратов расхождения Δрасх можно посчитать расчетное значение критерия согласия Пирсона:
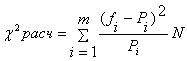 (26)
(26)
На полигоне частот (рисунок 11) показаны значения частоты распределения чисел по интервалам и вероятностей попадания в эти интервалы.
Теоретическое значение критического значения критерия Пирсона при уровне значимости α=0.1 и числом степеней свободы r=m-1 рассчитаем по формуле (11).
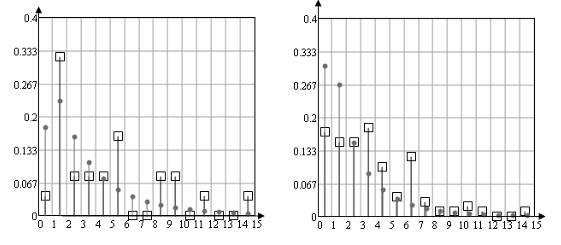
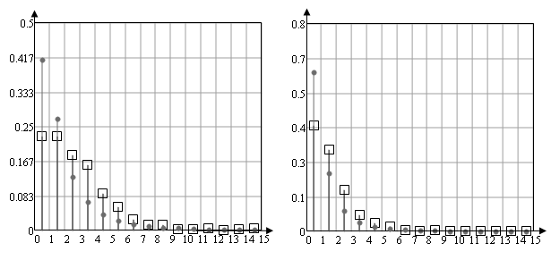
Рисунок 11.
(На рисунке показано расхождения между частотой попадания случайной величины в интервал и функцией распределения для попадания в этот интервал для выборок 25, 100, 500 и 1500. Случайная величина распределена по логнормальному закону распределения).
Ставится гипотеза: H0 – расхождение между прогнозом и трендом распределено по логнормальному закону
| Количество экспериментов | Критическое значение χ² | Эмпирическое значение χ² | Решение |
| 25 | 21.064 | 26.135 | Гипотеза H0 отвергается |
| 100 | 21.064 | 65.549 | Гипотеза H0 отвергается |
| 500 | 21.064 | 102.753 | Гипотеза H0 отвергается |
| 1500 | 21.064 | 241.778 | Гипотеза H0 отвергается |

Рисунок 12.
(На рисунке показано расхождения между частотой попадания случайной величины в интервал и функцией распределения для попадания в этот интервал для выборок 25, 100, 500, 1500 и 10000. Случайная величина распределена по нормальному закону распределения, для проверки взято теоретическое распределение с параметрами mx=0 и Dx=1).
Поставим гипотезу: H0 – расхождение между прогнозом и трендом распределено по нормальному закону распределения (с параметрами mx=0 и Dx=1).
| Количество экспериментов | Критическое значение χ² | Эмпирическое значение χ² | Решение |
| 25 | 21.064 | 14.865 | Гипотеза H0 принимается |
| 100 | 21.064 | 10.266 | Гипотеза H0 принимается |
| 500 | 21.064 | 9.161 | Гипотеза H0 принимается |
| 1500 | 21.064 | 32.575 | Гипотеза H0 отвергается |
| 10000 | 21.064 | 114.286 | Гипотеза H0 отвергается |
Отвержение гипотезы H0 о распределении случайной величины по нормальному закону при выборках 1500 и 10000 с параметрами mx=0 и Dx=1 свидетельствует об изменении параметров закона распределения (т.к. нормальный закон устойчив к линейным преобразованиям и сам закон не меняется), что является следствием линейных преобразований. Используем для проверки гипотезы о законе распределения с помощью критерия Пирсона теоретический закон распределения с дисперсией, равной оценке дисперсии отклонения прогноза от тренда, вычисленной по методу моментов.


Рисунок 13.
(На рисунке показано расхождения между частотой попадания случайной величины в интервал и функцией распределения для попадания в этот интервал для выборок 25, 100, 500, 1500 и 10000. Случайная величина распределена по нормальному закону распределения, для проверки взято теоретическое распределение с параметрами mx=0 и Dx= DΔ (DΔ =1.343; 1.149; 1,235; 1.158; 1.141)).
Поставим новую гипотезу: H0 – расхождение между прогнозом и трендом распределено по нормальному закону распределения (с параметрами mx=0 и Dx=DΔ).
| Количество экспериментов | Критическое значение χ² | Эмпирическое значение χ² | Решение |
| 25 | 21.064 | 12.251 | Гипотеза H0 принимается |
| 100 | 21.064 | 11.616 | Гипотеза H0 принимается |
| 500 | 21.064 | 11.503 | Гипотеза H0 принимается |
| 1500 | 21.064 | 14.31 | Гипотеза H0 принимается |
| 10000 | 21.064 | 11.275 | Гипотеза H0 принимается |
Заключение
а) на основании проведенных экспериментов и анализа полученных данных можно сделать вывод, подтверждающий, что логнормальное распределение является неустойчивым к линейным преобразованиям, причем с ростом числа наблюдений расхождение будет существенно возрастать;
б) при аппроксимации линейного тренда, к которому был добавлен шум, распределенный по логнормальному закону распределение все прямые, построенные по методу наименьших квадратов, всегда проходили выше прямой тренда. Это является следствием влияния ошибки наблюдений, которая была положительной величиной и говорит о том, что эффективность метода наименьших квадратов при аппроксимации тренда с положительной ошибкой наблюдений ниже, чем при аппроксимации тренда с ошибкой наблюдения, имеющее разные знаки;
в) при аппроксимации линейного тренда, к которому был добавлен шум, распределенный по нормальному закону, распределение отклонения прогноза от тренда так же подчинено нормальному закону распределения, в силу устойчивости последнего к линейным преобразованиям, но, из-за преобразований меняется его дисперсия (в нашем случае увеличивается в среднем на 12%), что было экспериментально подтверждено с использованием критерия Пирсона.
Список использованных источников
1. В.В. Бомас, В.С. Булыгин «Элементы теории Марковских процессов и ее технические приложения».
2. Феллер «Введение в теорию вероятностей и ее приложения»
3. Е.С. Вентцель «Теория вероятностей».
Похожие работы
... рассчитать коэффициент парной регрессии, не решая системы уравнений. Ясно также, что если рассчитаны линейные регрессии х(у) и у(х), то произведение коэффициентов dx и by, равно r2: (7)[1] Взвешенный метод наименьших квадратов Далеко не все задачи исследования взаимосвязей экономических переменных описываются обычной линейной регрессионной моделью. Во-первых, исходные данные могут не ...
... Как видно из таблиц, обнаружилась автокорреляция только первого и второго порядков. Это говорит о том, что значительное влияние на урожайность озимой пшеницы в данном году оказывает урожайность двух предыдущих лет. 3. Метод экспоненциального сглаживания Выберем теперь форму зависимости (линейную или параболическую) методом экспоненциального сглаживания. Рассчитаем начальные условия ...
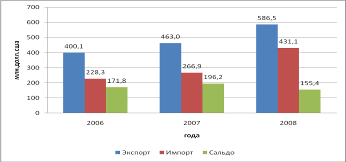
.1 Общая картина внешнеэкономической деятельность в Автономной Республике Крым в 2008 году По состоянию на 01.01.2009г. объёмы экспорта товаров в Автономной Республике Крым составили 586,5 млн.долл.США, импорта – 431,1 млн.долл.США. По сравнению с 2007 годом объёмы экспорта увеличились на 26,7%, импорта – в 1,6 раза. Положительное сальдо внешней торговли товарами составило 155,4 млн.долл. (в ...
... , проблема научного предусмотрения охватывает как теоретико-познавательный аспект, связанный с исследованием прогнозов как функции законов и теории наук, так и практический аспект, который выражается, в частности, в непосредственной связи прогнозирования с планированием и управлением.(11) 3.3 Классификация методов прогнозирования Методы прогнозирования можно разделить на две группы. Это ...



0 комментариев