Навигация
Синтез робастного регулятора матричным методом
3. Синтез робастного регулятора матричным методом.
Одним из возможных и перспективных способов решения задачи синтеза регуляторов является использования метода матричных операторов. Достоинством данного метода является возможность его применения для различных классов систем, в том числе нелинейных и нестационарных.
Рассмотрим линейную систему без неопределенности, описываемую в форме матричных операторов:
Очевидно, что для линейной системы без неопределенности справедливы следующие зависимости: ![]() ;
; ![]() ;
; ![]() .
.
Получаем следующую формулу расчета спектральной характеристики выходного сигнала: ![]()
Спектральная характеристика невязки между эталонной и реальной переходными характеристиками имеет вид:
![]() ,
,
где ![]() – варьируемые параметры корректирующих устройств, подлежащие определению.
– варьируемые параметры корректирующих устройств, подлежащие определению.
В приведенной формуле используется зависимость ![]() , усложняющая вычислительный процесс. Можно воспользоваться другим, более простым подходом. Определим спектральную характеристику невязки следующим образом:
, усложняющая вычислительный процесс. Можно воспользоваться другим, более простым подходом. Определим спектральную характеристику невязки следующим образом:
![]() .
.
Перейдем к системе с неопределенностью:
![]() ,
,
где ![]() – матричный оператор объекта, элементы которого зависят от
– матричный оператор объекта, элементы которого зависят от ![]() .
.
Необходимо минимизировать целевую функцию вида: 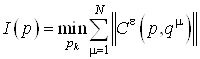 ,
,
где ![]() – число элементов выборки.
– число элементов выборки.
Полученный функционал содержит полную информацию о параметрической неопределенности.
В качестве корректирующего устройства выберем ПИД-регулятор:
![]() .
.
Пусть выборка составляет 1000 элементов. В качестве эталонного сигнала выберем ![]() . В качестве ортонормированного базиса выберем систему функций Уолша (128 функций). Интервал исследования –
. В качестве ортонормированного базиса выберем систему функций Уолша (128 функций). Интервал исследования – ![]() .
.
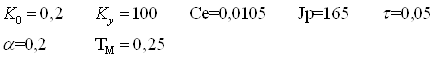 имеют интервальную неопределённость 20%
имеют интервальную неопределённость 20%
Приведем здесь клетку ![]() матричного оператора интегрирования:
матричного оператора интегрирования:

Получены следующие значения коэффициентов регулятора:
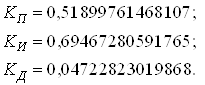
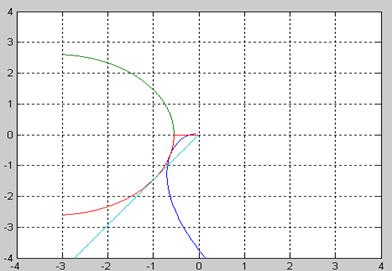
Несколько примеров для произвольно взятых ![]() , на которых представлены переходные характеристики эталонной системы и 4-х из семейства систем представлены на рис. 13.
, на которых представлены переходные характеристики эталонной системы и 4-х из семейства систем представлены на рис. 13.
![]()
![]()
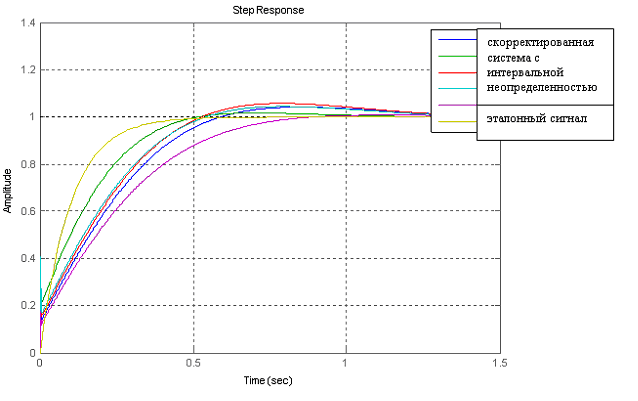
Рис. 13. Графики эталонной и реальной переходных характеристик для разных значений параметра ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]()
Приложение.
Программа 1.
Решения уравнения методом Стеффенсена.
function Stefens
clc
e=10.^-5;
x=-20;
x1=0;
i=0;
As=0.0125*(x.^3)+0.3*(x.^2)+4.886*x+61.72;
x=x-(As.^2)./((0.0125*((x+As).^3)+0.3*((x+As).^2)+4.886*(x+As)+61.72)+As);
As=0.0125*(x.^3)+0.3*(x.^2)+4.886*x+61.72;
A(1)=x;
i=i+1;
while abs(x-x1)>e
x1=x;
x=x-(As.^2)./((0.0125*((x+As).^3)+0.3*((x+As).^2)+4.886*(x+As)+61.72)+As);
As=0.0125*(x.^3)+0.3*(x.^2)+4.886*x+61.72;
A(i+1)=x;
i=i+1;
end
plot(1,A(1));
hold on
for n=1:i
plot(n,A(n),'b-o')
end
grid on
xlabel('iteraciya')
ylabel('roots')
disp('ответ');
disp(x);
disp('число итераций');
disp(i);
Программа 2.
Решение дифференциального уравнения численным способом.
clc
a2=24;
a1=390.88;
a0=4937.6;
b2=0;
b3=0;
b1=230.88;
b0=4617.6;
f1=b2;
f2=b1-a1*f1;
f3=b0-a1*f1-a2*f2;
B=[f1;f2;f3]
A=[0 1 0; 0 0 1;-a0 -a1 -a2]
h=0.02;
Xt=[0;0;0];
X(1,1)=Xt(1);
X(1,2)=Xt(2);
X(1,3)=Xt(3);
F=A*Xt+B;
% Разгонный метод
K1=h*F;t(1)=0;
K2=h*(F+K1/3);
K3=h*(F+K2/6+K1/6);
K4=h*(F+K1/8+3/8*K2);
K5=h*(F+K1/2-3/2*K3+2*K4);
Xt=Xt+(1./6)*(K1+4*K4+K5);
X(2,1)=Xt(1);
X(2,2)=Xt(2);
X(2,3)=Xt(3);
t(2)=t(1)+h;
F=A*Xt+B;
i=2;
%Неявный метод второго порядка
while t(i)<1.6
X1(1)=X(i-1,1);
X1(2)=X(i-1,2);
X1(3)=X(i-1,3);
Xt=Xt+(h./12)*(5*B+8*(A*Xt+B)-(A*X1'+B));
Xt=((eye(3)-(5./12)*h*A)^-1)*Xt;
X(i+1,1)=Xt(1);
X(i+1,2)=Xt(2);
X(i+1,3)=Xt(3);
t(i+1)=t(i)+h;
i=i+1;
end
h=0.9352-0.0629*exp(-17.6849*(t))-(0.8723*cos(16.4082*(t))-0.2357*sin(16.4082*(t))).*exp(-3.1576*(t));
for j=1:i
V(j)=X(j,1);
end
E=h-V;
plot(t,V,t,h,t,E); grid on
Программа 3.
Анализа заданной системы с использованием спектрального метода.
syms t T;
Kx=(4937.6./2)*(t-T).^2-390.88*(1./2)*(-2*(t-T))+24;
Ky=(4617.6./2)*(t-T).^2-230.88*(1./2)*(-2*(t-T));
for i=0:9
F6=0;
for j=0:i
m=i;
K=(sqrt(1.1552)*exp(-(1.1552*t)./2));
F=(factorial(m))./(factorial(m-j));
F1=((-1.1552*t).^j);
F2=(factorial(j)).^2;
F3=K.*F;
F4=F1./F2;
F5=F3.*F4;
F6=F6+F5;
L(i+1)=F6;
end
end
for i=0:9
F6=0;
for j=0:i
m=i;
K=(sqrt(1.1552)*exp(-(1.1552*T)./2));
F=(factorial(m))./(factorial(m-j));
F1=((-1.1552*T).^j);
F2=(factorial(j)).^2;
F3=K.*F;
F4=F1./F2;
F5=F3.*F4;
F6=F6+F5;
L1(i+1)=F6;
end
end
G=L'*L1;
In=Kx*G;
r=int(In,T,0,t);
Cx=int(r,t,0,1.5);
In=Ky.*G;
r=int(In,T,0,t);
Cy=int(r,t,0,1.5);
A=((Cx+eye(10))^-1)*Cy;
Cy=int(L,t,0,1.5);
Cx=A*Су'
function H=fun(t)
Cx=[-0.1275; 0.5090; 0.2483; 0.0697; -0.0459; -0.1140; -0.1472; -0.1555; -0.1468; -0.1275];
for i=0:9
F6=0;
for j=0:i
m=i;
K=(sqrt(1.1552)*exp(-(1.1552*t)./2));
F=(factorial(m))./(factorial(m-j));
F1=((-1.1552*t).^j);
F2=(factorial(j)).^2;
F3=K.*F;
F4=F1./F2;
F5=F3.*F4;
F6=F6+F5;
L(i+1)=F6;
end
end
H=(Cx'*L');
Программа 3.
Минимизация функционала.
function K=minF(X)
% Kn=X(1);
% Ku=X(2);
% Kd=X(3);
X=[0.7;
0.7;
0.7];
Kn=X(1);
Ku=X(2);
Kd=X(3);
clc
%--ПЕРЕМЕННЫЕ--%
e=0.0001;
l=1;
t=0;
h=0.001;
J1=1;
J=0;
J2=-1;
I=11;
I1=32;
alph=-10;
Xe=1-exp(alph*t);
H=eye(3);
H1=H;
Kn1=Kn+10^-3;
Kd1=Kd+10^-3;
Ku1=Ku+10^-3;
X1=[Kn1;Ku1;Kd1];
while (abs(J1-I)>e)
%--ГРАДИЕНТ--%
X3=[Kn;Ku;Kd];
U=Dif2([X3]);
J1=0;
i=1;
t=0;
while (t<2)
J1=J1+(1-exp(alph*t)-U(i))^2;
t=t+h;
i=i+1;
end
X3=[Kn+10^-3;Ku;Kd];
U=Dif2([X3]);
J=0;
i=1;
t=0;
while (t<2)
J=J+(1-exp(alph*t)-U(i))^2;
t=t+h;
i=i+1;
end
g1=(J-J1)/10^-3;
X3=[Kn;Ku+10^-3;Kd];
U=Dif2([X3]);
J=0;
t=0;
i=1;
while (t<2)
J=J+(1-exp(alph*t)-U(i))^2;
t=t+h;
i=i+1;
end
g2=(J-J1)/10^-3;
X3=[Kn;Ku;Kd+10^-3];
U=Dif2([X3]);
J=0;
t=0;
i=1;
while (t<2)
J=J+(1-exp(alph*t)-U(i))^2;
t=t+h;
i=i+1;
end
g3=(J-J1)/10^-3;
I1=J;
GradJ=[g1;g2;g3];
%--НОВОЕ ЗНАЧЕНИЕ Х--%
X1=X1-l*H*GradJ;
X=X1;
Kn1=X(1);
Ku1=X(2);
Kd1=X(3);
Kn=Kn1;
Ku=Ku1;
Kd=Kd1;
X3=[Kn;Ku;Kd];
U=Dif2([X3]);
J1=0;
i=1;
t=0;
while (t<2)
J1=J1+(1-exp(alph*t)-U(i))^2;
t=t+h;
i=i+1;
end
X3=X1+[10^-3;0;0];
U=Dif2([X3]);
J=0;
t=0;
i=1;
while (t<2)
J=J+(1-exp(alph*t)-U(i))^2;
t=t+h;
i=i+1;
end
g11=(J-J1)/10^-3;
X3=X1+[0;10^-3;0];
U=Dif2([X3]);
J=0;
t=0;
i=1;
while (t<2)
J=J+(1-exp(alph*t)-U(i))^2;
t=t+h;
i=i+1;
end
g21=(J-J1)/10^-3;
X3=X1+[0;0;10^-3];
U=Dif2([X3]);
J=0;
t=0;
i=1;
while (t<2)
J=J+(1-exp(alph*t)-U(i))^2;
t=t+h;
i=i+1;
end
I=J;
g31=(J-J1)/10^-3;
GradJ1=[g11;g21;g31];
U1=GradJ1-GradJ;
V=l*H*GradJ;
A=(V*V')/(V'*U1);
B=-(H*U1*U1')/(U1'*H*U1);
H1=H+A+B;
if J1>I
l=min_lz(X,l,H,GradJ);
X1=X;
end
X=X1;
Kn1=X(1);
Ku1=X(2);
Kd1=X(3);
Kn=Kn1;
Ku=Ku1;
Kd=Kd1;
end
Kn
Ku
Kd
function la=min_l(X,l,H,GradJ)
b=1;
a=0;
e=0.05;
x4=10;
x2=a+(-1+sqrt(1+4*(b-a)))/(2);
while (abs(x2-x4)>e)
x4=a+b-x2;
F2=X-x2*H*GradJ;
F4=X-x2*H*GradJ;
if norm(F2)<norm(F4)
b=x4;
else
x2=x4;
a=x2;
end
end
X=[0.43101603658062
0.78399472393963
0.05296602599762];
Kn=X(1);
Ku=X(2);
Kd=X(3);
a4=693/693;
a3=(160000*Kd+16632)/693;
a2=(110880+160000*Kn+3200000*Kd)/693;
a1=(160000*Ku+221760+3200000*Kn)/693;
a0=3200000*Ku/693;
b4=0;
b3=160000*Kd/693;
b2=(3200000*Kd+160000*Kn)/693;
b1=(3200000*Kn+160000*Ku)/693;
b0=3200000*Ku/693;
H=tf([b4 b3 b2 b1 b0],[a4 a3 a2 a1 a0]);
h=tf([10],[1 10]);
ltiview(H,h);
function Xre=Dif2(X)
Kn=X(1);
Ku=X(2);
Kd=X(3);
a4=693/693;
a3=(160000*Kd+16632)/693;
a2=(110880+160000*Kn+3200000*Kd)/693;
a1=(160000*Ku+221760+3200000*Kn)/693;
a0=3200000*Ku/693;
b4=0;
b3=160000*Kd/693;
b2=(3200000*Kd+160000*Kn)/693;
b1=(3200000*Kn+160000*Ku)/693;
b0=3200000*Ku/693;
f0=b4;
f1=b3-a3*f0;
f2=b2-a2*f0-a3*f1;
f3=b1-a1*f0-a2*f1-a3*f2;
f4=b0-a0*f0-a1*f1-a2*f2-a3*f3;
B=[f1;f2;f3;f4];
A=[0 1 0 0;
0 0 1 0;
0 0 0 1;
-a0 -a1 -a2 -a3];
h=0.001;
Xt=[0;0;0;0];
X(1,1)=Xt(1);
X(1,2)=Xt(2);
X(1,3)=Xt(3);
X(1,4)=Xt(4);
F=A*Xt+B;
% Разгонный метод
K1=h*F;t(1)=0;
K2=h*(F+K1/3);
K3=h*(F+K2/6+K1/6);
K4=h*(F+K1/8+3/8*K2);
K5=h*(F+K1/2-3/2*K3+2*K4);
Xt=Xt+(1./6)*(K1+4*K4+K5);
X(2,1)=Xt(1);
X(2,2)=Xt(2);
X(2,3)=Xt(3);
X(2,4)=Xt(4);
t(2)=t(1)+h;
F=A*Xt+B;
i=2;
%Неявный метод второго порядка
while t(i)<5
X1(1)=X(i-1,1);
X1(2)=X(i-1,2);
X1(3)=X(i-1,3);
X1(4)=X(i-1,4);
Xt=Xt+(h./12)*(5*B+8*(A*Xt+B)-(A*X1'+B));
Xt=((eye(4)-(5./12)*h*A)^-1)*Xt;
X(i+1,1)=Xt(1);
X(i+1,2)=Xt(2);
X(i+1,3)=Xt(3);
X(i+1,4)=Xt(4);
t(i+1)=t(i)+h;
i=i+1;
end
for j=1:i
V(j)=X(j,1);
end
Xre=V;
Программа 4.
Синтез робастного регулятора.
function I=Robsist(X)
Kp=X(1);
Ku=X(2);
Kd=X(3);
clc
N=128; %Число функций Уолша
% syms Kp Ku Kd;
m=1000;
T=1.5;
h=T/(N-1);
K0=0.2*(0.8+0.4*rand(m,1));
Ky=100*(0.8+0.4*rand(m,1));
Ce=0.0105*(0.8+0.4*rand(m,1));
Jp=165*(0.8+0.4*rand(m,1));
ta=0.05*(0.8+0.4*rand(m,1));
al=0.2*(0.8+0.4*rand(m,1));
Tm=0.25*(0.8+0.4*rand(m,1));
Int=m_intM(T,N);
I=eye(N);
H=hadamard(N); %построение матрицы Адамара
for i=0:(N-1)
t=i*h;
f(i+1)=y(t);
end
Cy=(1/sqrt(N)*H)*f';%спектр входа
for i=0:(N-1)
t=i*h;
f(i+1)=xe(t); %эталонный выход
end
Cx=(1/sqrt(N)*H)*f';%спектр эталонного выхода
for k=1:m
a4=Ce(k)*Tm(k)*ta(k);
a3=(Ky(k)*Jp(k)*Kd*ta(k)+Ce(k)*Tm(k)+Ce(k)*ta(k));
a2=(Ce(k)*Ky(k)*Jp(k)^2*K0(k)*ta(k)+Ky(k)*Jp(k)*Kd+Ky(k)*Jp(k)*Kp*ta(k)+Ce(k));
a1=(Ce(k)*Ky(k)*Jp(k)^2*K0(k)*al(k)+Ky(k)*Jp(k)*Ku*ta(k)+Ky(k)*Jp(k)*Kp);
a0=Ky(k)*Jp(k)*Ku;
b3=Ky(k)*Jp(k)*Kd*ta(k);
b2=(Ky(k)*Jp(k)*Kp*ta(k)+Ky(k)*Jp(k)*Kd);
b1=(Ky(k)*Jp(k)*Ku*ta(k)+Ky(k)*Jp(k)*Kp);
b0=Ky(k)*Jp(k)*Ku;
E=(a4*I+a3*Int+a2*Int*Int+a1*Int*Int*Int+a0*Int*Int*Int*Int)*Cx-(b3*Int+b2*Int*Int+b1*Int*Int*Int+b0*Int*Int*Int*Int)*Cy;
E1(k)=E'*E;
end
I=sum(E1(k));
X=[0.05189976146807 0.39467280591765 0.00047228019868];
Kp=X(1);
Ku=X(2);
Kd=X(3);
m=100;
K0=0.2*(0.8+0.4*rand(m,1));
Ky=100*(0.8+0.4*rand(m,1));
Ce=0.0105*(0.8+0.4*rand(m,1));
Jp=165*(0.8+0.4*rand(m,1));
ta=0.05*(0.8+0.4*rand(m,1));
al=0.2*(0.8+0.4*rand(m,1));
Tm=0.25*(0.8+0.4*rand(m,1));
for k=1:m
a4=Ce(k)*Tm(k)*ta(k);
a3=(Ky(k)*Jp(k)*Kd*ta(k)+Ce(k)*Tm(k)+Ce(k)*ta(k));
a2=(Ce(k)*Ky(k)*Jp(k)^2*K0(k)*ta(k)+Ky(k)*Jp(k)*Kd+Ky(k)*Jp(k)*Kp*ta(k)+Ce(k));
a1=(Ce(k)*Ky(k)*Jp(k)^2*K0(k)*al(k)+Ky(k)*Jp(k)*Ku*ta(k)+Ky(k)*Jp(k)*Kp);
a0=Ky(k)*Jp(k)*Ku;
b3=Ky(k)*Jp(k)*Kd*ta(k);
b2=(Ky(k)*Jp(k)*Kp*ta(k)+Ky(k)*Jp(k)*Kd);
b1=(Ky(k)*Jp(k)*Ku*ta(k)+Ky(k)*Jp(k)*Kp);
b0=Ky(k)*Jp(k)*Ku;
H(k)=tf([b3 b2 b1 b0],[a4 a3 a2 a1 a0]);
end
h=tf([10],[1 10]);
ltiview(H(1),H(10),H(45),H(78),H(58),h);
Литература.
1. Вержбитский Численные методы. – М.: Наука, 1987
2. Методы классической и современной теории автоматического управления: Учебник в 5-ти т.; 2-е изд., перераб. и доп. Т.3: Синтез регуляторов систем автоматического управления / Под редакцией К.А. Пупкова и Н.Д. Егупова. – М.: Издательство МГТУ им. Н.Э. Баумана, 2004. – 616с.; ил.
Похожие работы
... Национальный Технический Университет Кафедра Технической кибернетики ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовому проекту по курсу «Проектирование систем автоматического управления» «Проектирование системы автоматического регулирования угла поворота вала электродвигателя» Выполнила: ст. гр. А – 61з Брусинов С. Э. Проверил: Дубовик С.А. Оценка ________________ Дата «____» ...
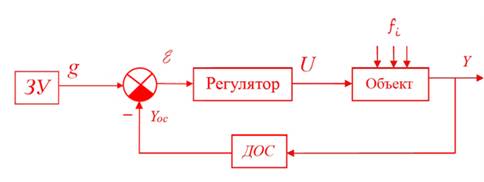
... поведение регулируемой величины. Управляющее воздействие вырабатывается устройством управления (УУ). Совокупность взаимодействующих управляющего устройства и управляемого объекта образует систему автоматического управления. Система автоматического управления (САУ) поддерживает или улучшает функционирование управляемого объекта. В ряде случаев вспомогательные для САУ операции (пуск, остановка, ...
... регулятор на нелинейный элемент. В качестве нелинейного элемента возьмём идеальное реле, статическая характеристика звена изображена на рисунке 23. Рис.23. Идеальное реле Чтобы реализовать данный регулятор в заданной системе автоматического управления, требуется рассчитать значения параметра с. Проанализируем работу системы с нелинейной характеристикой и без неё в Simulink, а затем найдём ...
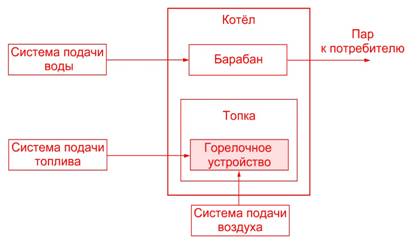
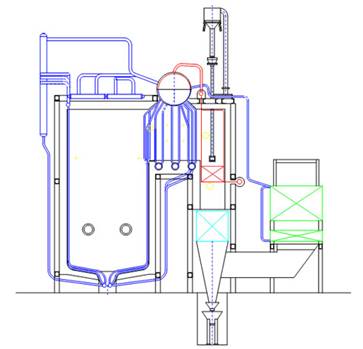
... режимов функционирования котла. Повышение экологических характеристик котельной и культуру производственного процесса. Благодаря программному управлению система автоматически отслеживает все параметры текущих процессов, реализуемых водогрейными и паровыми котлами, и управляет технологическим оборудованием, обеспечивая нормальное и безаварийное функционирование котельной установки. Кроме того, ...

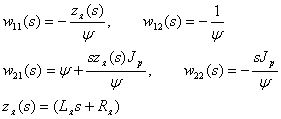

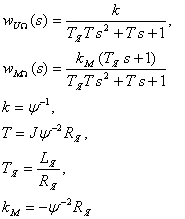




0 комментариев