Навигация
2. Квадратичные кривые
Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q0 и Q1 из условия чтобы параметр t изменялся от 0 до 1:
Точка Q0 изменяется от P0 до P1 и описывает линейную кривую Безье.
Точка Q1 изменяется от P1 до P2 и также описывает линейную кривую Безье.
Точка B изменяется от Q0 до Q1 и описывает квадратичную кривую Безье.
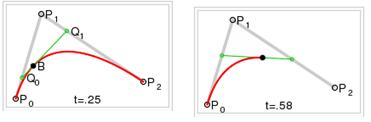
Рисунок 3 Построение квадратичной кривой Безье
3. Кривые высших степеней
Для построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки Q0, Q1 и Q2, описывающие линейные кривые, а также точки R0 и R1, которые описывают квадратичные кривые: более простое уравнение p0q0/p0q1=q1p1/p1p2=bq0/q1q0
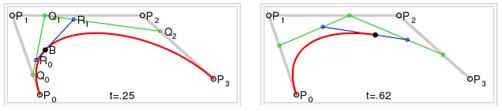
Рисунок 4 Построение кубической кривой Безье
Для кривых четвёртой степени это будут точки Q0, Q1, Q2 и Q3, описывающие линейные кривые, R0, R1 и R2, которые описывают квадратичные кривые, а также точки S0 и S1, описывающие кубические кривые Безье:
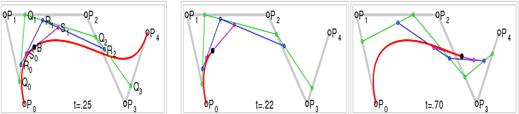
Рисунок 5 Построение кривой Безье 4-ой степени
1.4 Применение в компьютерной графике
Благодаря простоте задания и манипуляции, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые), а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение и др.) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.
Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, три смежные опорные точки обеих кривых должны лежать на одной прямой.
1.5 Преобразование квадратичных кривых Безье в кубические
Квадратичная кривая Безье с координатами ![]() преобразовывается в кубическую кривую Безье с координатами:
преобразовывается в кубическую кривую Безье с координатами:
![]()
2. Финитные функции
Финитной называется функция ![]() , определенная для всех
, определенная для всех ![]() , но отличная от нуля лишь на некоторой конечной области
, но отличная от нуля лишь на некоторой конечной области ![]() , называемой конечным носителем:
, называемой конечным носителем:
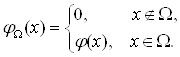 (2.1)
(2.1)
Для ![]() , определенных на
, определенных на ![]() , построение базиса
, построение базиса ![]() из финитных функций осуществляется следующим образом. Сначала область
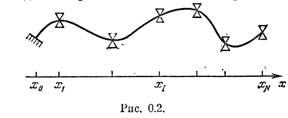
из финитных функций осуществляется следующим образом. Сначала область ![]() , в которой решается задача, некоторым регулярным образом покрывается конечным числом
, в которой решается задача, некоторым регулярным образом покрывается конечным числом ![]() перекрывающихся подобластей
перекрывающихся подобластей ![]() , например как на рис. 6.1:
, например как на рис. 6.1:
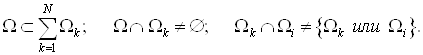 (2.2)
(2.2)
Желательно, чтобы ![]() только для
только для ![]() , смежных с
, смежных с ![]() .
.
Подобласти ![]() получили название конечные элементы.
получили название конечные элементы.
Затем на каждом ![]() как на конечном носителе строим базисную финитную функцию
как на конечном носителе строим базисную финитную функцию ![]() . Все функции таким образом выбранного базиса линейно независимы в силу условий (2.1), (2.2).
. Все функции таким образом выбранного базиса линейно независимы в силу условий (2.1), (2.2).
Отметим преимущества такого выбора базиса:
а) ввиду того, что ![]() выбираются значительно меньшими
выбираются значительно меньшими ![]() и при этом скалярные произведения
и при этом скалярные произведения
![]() (2.3)
(2.3)
равны нулю для функций с непересекающимися носителями, матрица проекционного уравнения будет сильно разрежена. Более того, если условие ![]() выполняется только для смежных носителей, то матрица получается ленточной, т.е. аналогична той, к которой приводят сеточные методы;
выполняется только для смежных носителей, то матрица получается ленточной, т.е. аналогична той, к которой приводят сеточные методы;
б) возможность выбора специфических приграничных конечных элементов и связанных с ними финитных функций, учитывающих особенности границы, позволяет эффективно решать краевые задачи на достаточно произвольной области ![]() .
.
Основная трудность аппроксимации финитными функциями состоит в сопряжении финитных функций на границах Wk таким образом, чтобы функция ![]() в целом была непрерывна вместе со своими производными достаточно высокого порядка.
в целом была непрерывна вместе со своими производными достаточно высокого порядка.
При таком выборе базиса естественно поставить вопросы о его полноте, выборе вида функций ![]() и аппроксимационных свойствах разложения искомого решения
и аппроксимационных свойствах разложения искомого решения
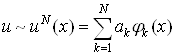 . (2.4)
. (2.4)
На все эти вопросы частично дает ответ теория Стренга-Фикса.
2.2 Теория аппроксимации финитными функциями Стренга-ФиксаИзложим основные идеи этой теории для функций одной переменной с регулярными конечными элементами.
Область ![]() покрываем равномерной сеткой
покрываем равномерной сеткой
![]() , [p] – целая часть p.
, [p] – целая часть p.
Конечные элементы ![]() выберем как отрезки длиной
выберем как отрезки длиной ![]() с центром в точке
с центром в точке ![]() :
: ![]() . Если
. Если ![]() , смежные элементы не пересекаются и их длина равна
, смежные элементы не пересекаются и их длина равна ![]() : если
: если ![]() , то длина пересечения равна
, то длина пересечения равна ![]() , длина
, длина ![]() равна
равна ![]() ; при
; при ![]() – длина пересечения
– длина пересечения ![]() , длина
, длина ![]() равна
равна ![]() . Заметим, что такое покрытие полностью удовлетворяет условиям (2.2). Все базисные финитные функции с носителями
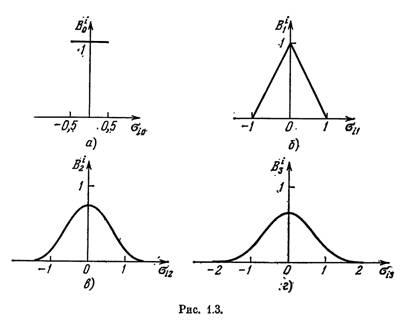
. Заметим, что такое покрытие полностью удовлетворяет условиям (2.2). Все базисные финитные функции с носителями ![]() выберем одинаковой формы как сдвиги одной «стандартной» финитной функции
выберем одинаковой формы как сдвиги одной «стандартной» финитной функции ![]() :
:
 ;
; 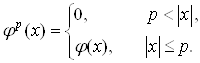 (2.5)
(2.5)
Если «стандартная» функция нормирована к единице, то ее сдвиги записываются в виде
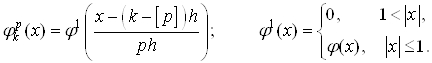 (2.6)
(2.6)
Теорема Стренга-Фикса (один из вариантов)
Допустим, что ![]() . В этом случае для
. В этом случае для ![]() существует преобразование Фурье:
существует преобразование Фурье:
прямое 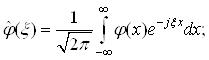 обратное
обратное 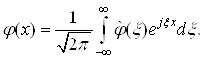
Допустим, что для преобразования Фурье стандартной финитной функции ![]() выполнено условие
выполнено условие
![]() и
и 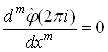 при
при ![]() (2.7)
(2.7)
(т.е. в ![]() точках
точках ![]() имеет нули
имеет нули ![]() й кратности).
й кратности).
Тогда существуют такие ![]() , что при
, что при ![]()
 .
.
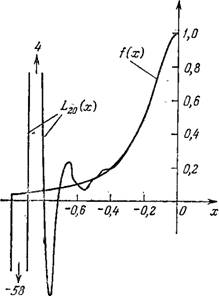
Это значит, что если, например, подобрать ![]() , у которой условия теоремы выполняются для
, у которой условия теоремы выполняются для ![]() , то аппроксимация самой функции
, то аппроксимация самой функции ![]() имеет порядок
имеет порядок ![]() , аппроксимация ее первой производной
, аппроксимация ее первой производной![]() , второй –
, второй – ![]() .
.
Наличие такой центральной теоремы, а также еще ряда доказанных Стренгом-Фиксом теорем, в частности о существовании функций, удовлетворяющих условиям (2.7), дает алгоритм для построения базисных финитных функций, обладающих необходимыми аппроксимационными свойствами.
Похожие работы
... в и представление (4) единственно. Эта формула называется представлением сплайна в виде суммы усеченных степенных функций. Итак, множество является конечномерным пространством размерности §2. Базисные сплайны с конечными носителями В математическом анализе встречаются конструкции, связанные с финитными функциями, т. е. гладкими функциями, которые определяются на всей действительной оси, ...
... часть пульта управления (или устройства вывода данных) оператора-рентгенолога. Аналогичные пульты управления можно применять и в других системах получения изображения, например на основе ядерного магнитного резонанса или компьютерной томографии. Цифровое изображение можно записать на магнитном носителе, оптическом диске или же на специальном записывающем устройстве, способном постоянно вести ...
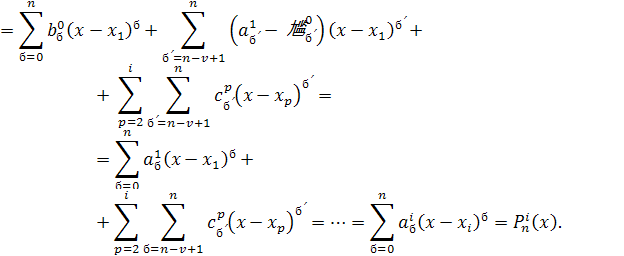
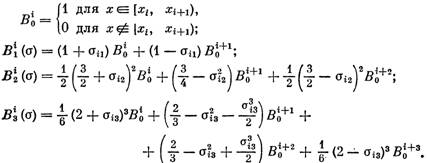
0 комментариев