Исследование методами математической статистики

2. Исследование методами математической статистики

1)  Общие методы математической статистики

Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надёжность и точность выводов, делаемых на основании ограниченного статистического материала (напр., оценить необходимый объём выборки для получения результатов требуемой точности при выборочном обследовании).

Математическая статистика — раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений[1]. В зависимости от математической природы конкретных результатов наблюдений статистика математическая делится на статистику чисел, многомерный статистический анализ, анализ функций (процессов) и временных рядов, статистику объектов нечисловой природы.

Выделяют описательную статистику, теорию оценивания и теорию проверки гипотез. Описательная статистика есть совокупность эмпирических методов, используемых для визуализации и интерпретации данных (расчет выборочных характеристик, таблицы, диаграммы, графики и т. д.), как правило, не требующих предположений о вероятностной природе данных. Некоторые методы описательной статистики предполагают использование возможностей современных компьютеров. К ним относятся, в частности, кластерный анализ, нацеленный на выделение групп объектов, похожих друг на друга, и многомерное шкалирование, позволяющее наглядно представить объекты на плоскости.

Методы оценивания и проверки гипотез опираются на вероятностные модели происхождения данных. Эти модели делятся на параметрические и непараметрические. В параметрических моделях предполагается, что характеристики изучаемых объектов описываются посредством распределений, зависящих от (одного или нескольких) числовых параметров. Непараметрические модели не связаны со спецификацией параметрического семейства для распределения изучаемых характеристик. В математической статистике оценивают параметры и функции от них, представляющие важные характеристики распределений (например, математическое ожидание, медиана, стандартное отклонение, квантили и др.), плотности и функции распределения и пр. Используют точечные и интервальные оценки.

Большой раздел современной математической статистики — статистический последовательный анализ, фундаментальный вклад в создание и развитие которого внес А. Вальд во время Второй мировой войны. В отличие от традиционных (непоследовательных) методов статистического анализа, основанных на случайной выборке фиксированного объема, в последовательном анализе допускается формирование массива наблюдений по одному (или, более общим образом, группами), при этом решение об проведении следующего наблюдения (группы наблюдений) принимается на основе уже накопленного массива наблюдений. Ввиду этого, теория последовательного статистического анализа тесно связана с теорией оптимальной остановки.

В математической статистике есть общая теория проверки гипотез и большое число методов, посвящённых проверке конкретных гипотез. Рассматривают гипотезы о значениях параметров и характеристик, о проверке однородности (то есть о совпадении характеристик или функций распределения в двух выборках), о согласии эмпирической функции распределения с заданной функцией распределения или с параметрическим семейством таких функций, о симметрии распределения и др.

Большое значение имеет раздел математической статистики, связанный с проведением выборочных обследований, со свойствами различных схем организации выборок и построением адекватных методов оценивания и проверки гипотез.

Задачи восстановления зависимостей активно изучаются более 200 лет, с момента разработки К. Гауссом в 1794 г. метода наименьших квадратов.

Разработка методов аппроксимации данных и сокращения размерности описания была начата более 100 лет назад, когда К. Пирсон создал метод главных компонент. Позднее были разработаны факторный анализ[2] и многочисленные нелинейные обобщения[3].

Различные методы построения (кластер-анализ), анализа и использования (дискриминантный анализ) классификаций (типологий) именуют также методами распознавания образов (с учителем и без), автоматической классификации и др.

В настоящее время компьютеры играют большую роль в математической статистике. Они используются как для расчётов, так и для имитационного моделирования (в частности, в методах размножения выборок и при изучении пригодности асимптотических результатов).

2)  Исследование выборочных статистических данных

Объем продаж компьютерной техники в магазине «Горбушкин двор» изменяется в зависимости от времени года, ассортимента товаров, цен производителя и т.д. Известны статистические данные этого показателя в течение некоторого времени.

1)  Необходимо сгруппировать данные, образовав 8-10 интервалов. Найти распределение частот и относительных частот .

2)  Найти и построить эмпирическую функцию распределения

Найдем эмпирическую функцию распределения по формуле:

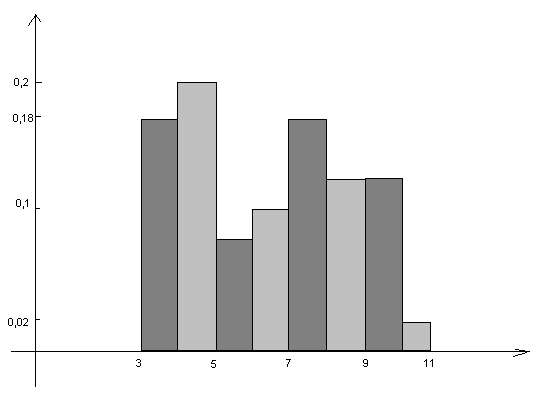
3)  Построить полигон распределения. Построить гистограмму частот и относительных частот распределения. Объяснить основное свойство гистограммы

4)  Выдвинуть гипотезу о вероятном распределении показателя. Найти точечные оценки числовых характеристик распределения

5)  Методом моментов найти оценку параметров распределения, считая его равномерным на заданном интервале значений

6)  Оценить истинные значения параметров выборочного распределения с помощью доверительного интервала с надежностью 0.95,считая распределение нормальным

7)  Использовать критерий Пирсона, при уровне значимости 0.05 проверить согласуется ли гипотеза о

а) нормальном распределении выборки

б) показательном распределении выборки

в) равномерном распределении выборки

1.  Сгруппировав данные получим 8 интервалов:

	[3;5)	[5;7)	[7;9)	[9;11)	[11;13)	[13;15)	[15;17)	[17;19]
	1	1	4	9	17	12	4	1

Найдем распределение частот:

	4	6	8	10	12	14	16	18
	1	1	4	9	17	12	4	1

 

Найдем распределение относительных частот

n= 1+1+4+9+17+12+4+1=49

	4	6	8	10	12	14	16	18
	0.02	0.02	0.08	0.18	0.35	0.24	0.082	0.02

2. 

 

1.  x(-

0

2.  x

=0.02

3.  x

=0.02+0.02=0.04

4.  x

=0.04+0.08=0.12

5.  x  

=0.12+0.18=0.3

6.  x

=0.3+0.35=0.65

7.  x

=0.65+0.24=0.89

8.  x

0.89+0.082=0.972

9.  x

0.97+0.02=1

Итак, эмпирическая функция распределения будет выглядеть так

 

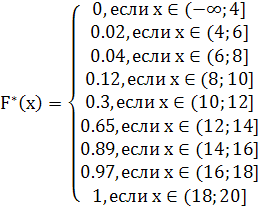
Построим эмпирическую функцию распределения

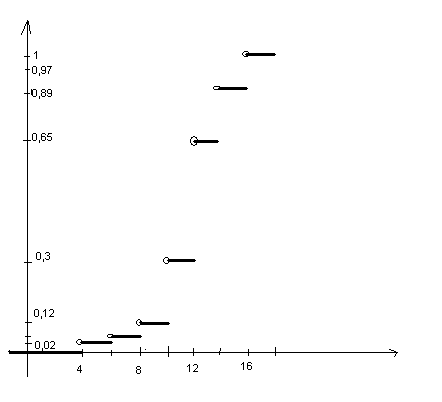
3. 

Полигон распределения

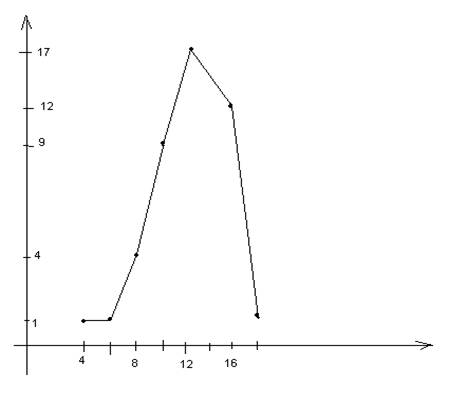
Гистограммой – называется фигура состоящая из прямоугольника . Основания прямоугольников – интервальные задания случайной величины, высота прямоугольников

-  для гистограммы частот находится по формуле:

=

=0.5

=0.5

 

 

-  для гистограммы относительных частот находится по формуле:

 

 

 

4.   .

5.  Метод моментов применяется для оценки неизвестных параметров распределения, суть методов заключается в том, что приравниваются теоретические и эмпирические моменты. Если закон распределения содержит 1 параметр, то для оценки этого параметра составляется одно уравнение, в котором теоретический момент приравнивают к эмпирическому моменту. Если распределение случайной величины содержит 2 параметра, то составляют два уравнения и т.д.

Считая распределение равномерным на заданном интервале значений запишем дифференциальный закон:

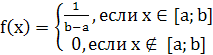 2 параметра распределения a и b

M(x)= 

D(x)=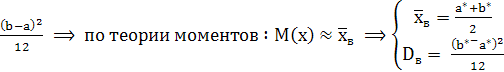

D(x)  

(4+6+32+90+204+168+64+18)==11.959

=

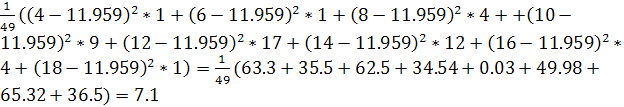
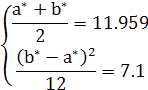
6. Доверительным называют интервал который с заданной надежностью  показывает заданный параметр.

Истинное значение измеряемой величины равно ее математическому ожиданию a. Поэтому задача сводится к оценке математического ожидания (при известном ) при помощи доверительного интервала

 = 2.009

Все величины кроме S(среднеквадратического отклонения) известны. Для нахождения S сначала найдем (исправленную дисперсию).

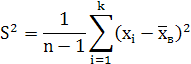
*175.4=3.58

=1.89

7. а) 1.

2. Вычислим теоретические частоты, учитывая, что n=49, h=1, =2.6, по формуле:

i
1	4	-3,06	0.0037	0,07
2	6	-2,29	0.0290	0,55
3	8	-1,52	0.1257	2,37
4	10	-0,75	0.3011	5,67
5	12	0,015	0.3989	7,52
6	14	0,78	0.2943	5,55
7	16	1,55	0.1200	2,26
8	18	2,32	0.0270	0,51