Навигация
1.3 Рішення задач
Задача 1. Що невірно в наступних міркуваннях? Оскільки n = O(n) і 2n = O(n) і так далі, те містимо, що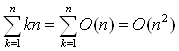 
?
Рішення:
Заміна kn на O(n) має на увазі різні Із для різних k; а потрібно, щоб усе О мали загальну константу. У дійсності, у цьому випадку потрібно, щоб О позначало множину функцій двох змінних, k і n. Правильно буде записати
.
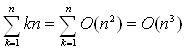Задача 2. Доведіть або спростуйте: О(f(n) + g(n)) = f(n) + O(g(n)), якщо f(n) і g(n) позитивні для всіх nÎN.
Рішення:
Твердження невірне.
Нехай f(n) = n2, а g(n) = 1. Знайдемо таку функцію j(n), яка б належала лівій множині, але не належала б правій множині, тобто ($З1) ("n) [j(n) £ C1(n2 + 1)] і ("З2) ($n³n0) [j(n) > n2 + C2].
Візьмемо j(n) = 2n2.
1). Нехай З1 = 3, тоді ("n³n0) 2n2 £ 3(n2 + 1). Значить функція j(n) належить лівій множині.
2). ("З2) ($n>
) 2n2 > n2 + C2. Значить функція j(n) не належить правій множині.
Задача 3. Доведіть або спростуйте: cos O(x) = 1 + O(x2) для всіх речовинних х.
Рішення:
Якщо функція g(x) належить лівій частині так, що g(x) = cos y для деякого y, причому 
для деякої константи З, то g(x) = cos y = 1 - 2sin2 (y/2) £ 1 = 1 + 0 × х2. Значить існує така константа В, що g(x) £ 1 + В × х2. Отже, множина з лівої частини втримується в правій частині, і формула вірна.
Задача 4. Доведіть, що 
.
Рішення:
Перетворимо ліву частину в такий спосіб:
.
Помітимо, що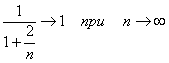 
, тоді 
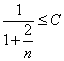, де З – константа, тоді можна записати по визначенню символу О, що 
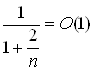. Використовуючи це для перетвореної рівності, одержуємо, що
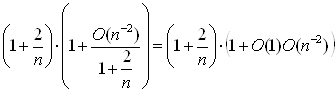= (по 1.2.4)
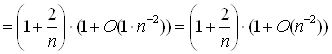
Що й було потрібно довести.
Задача 5. Обчислите 
при nÎN.
Рішення:
(по 1.2.6)
(по 1.2.3)
(по 1.2.4)
(по 1.2.2)
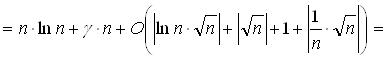
Задача 6. Обчислите (n + 2 + O(n-1))n з відносною погрішністю O(n-1), при n®¥.
Рішення:
(по 1.2.3 і 1.2.4)
При n®¥ k = (2n-1 + O(n-2)) ® 0, тоді ln (1 + k) ® 0. Тоді при n®¥ ln (1 + k) = k.
(по 1.2.9)
.
Задача 7. Доведіть, що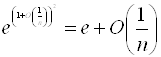 
, при nÎN, n®¥.
Рішення:
Покажемо, що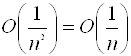 
.(*)
По визначенню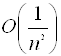 
- функція аn така, що 
.
Одержуємо, що 
, значить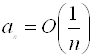 
.
Тепер доведемо, що :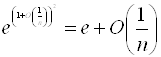
= (по 1.2.4 і 1.2.6) = 
= (по (*)) =
(по 1.2.6) = 
(по 1.2.9) =
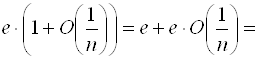(по 1.2.6) =
.
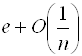Розділ 2. Додаток символу О
Похожие работы
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
ерел). Розділ 1. Соціологічні підходи до вивчення особистості та її місця в суспільстві 1.1 Зміст поняття «особистість» – соціологічне визначення Особистість як соціальна якість людини є предметом соціальних наук: філософії, соціології, психології та ін. Соціологія досліджує особистість як суб'єкт соціальних відносин, виділяючи в ній соціально-типові характеристики, які розвиваються ...
... й зрозумілими символами. Завдяки цьому звуки засвоюються природним шляхом, без натиску й перевантажень, корекційно-навчальний процес стає цікавим і доступним для всіх дітей-логопатів. Розділ II. Використання символів на логопедичних заняттях Дитині значно легше засвоїти поняття, коли воно не тільки показане логопедом на собі, а й позначене зрозумілим, близьким для дитини образом, легким для ...
... залишаються до кінця незбагненними, невичерпними в своїй суттєвій архітектоніці. Якщо говорити про ступінь наукового опрацювання проблеми пошуку відповіді на питання про визначення методологічних та гносеологічних основ вивчення феномена безсмертя, то вона взагалі досліджена тільки фрагментарно і досі лишається недостатньо розробленою. Дослідницька література, що вплинула на формування загальної ...
0 комментариев