Асимптотичне рішення інтегралів

2.2 Асимптотичне рішення інтегралів

Приклад 1. Обчислити  при х > 1.

Розкладемо в ряд [6]:

По теоремі (2.1.2)

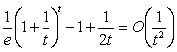, тобто .

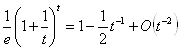Приклад 2. Обчислити  при e®+0, , А(х) - східчаста функція: А(х) = 0 при х < 0, А(х) = А_k, k £ x < k + 1, А_k = а₁ + а₂ +…+а_k , а_k = k ^-1 . Причому .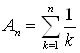

Скористаємося асимптотичною формулою [4]

,

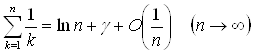де g - постійна Ейлера 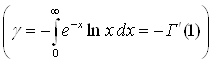. Уведемо функцію Ã(х) = lnx + g.

.

Останній інтеграл має порядок О(e ln e) при e®+0, а передостанній – дорівнює -g/2, так що

.

S(e) = I + J, де

.

Оцінимо інтеграл J. Нехай 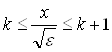, тоді " k ³ 1

.

Ологарифмуємо 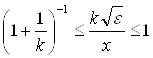, одержимо .

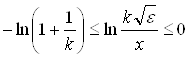Значить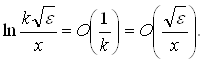

Отже,

.

Одержуємо, що

.

2.3 Асимптотичне обчислення суми ряду

При знаходженні суми ряду нерідко використовується формула підсумовування Ейлера [2]:

де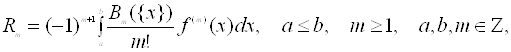

В_k – числа Бернуллі, В_m({x}) – багаточлен Бернуллі.

В_k = (-1)^k b_2k. [6]

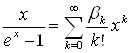. Коефіцієнти b_k обчислюються, використовуючи теорему О одиничність розкладання функції в статечної ряд:

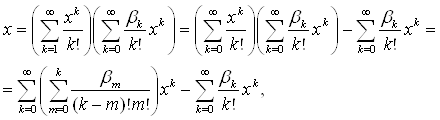
шляхом дорівнюючи коефіцієнтів:

коефіцієнт при х: b₀ = 1,

коефіцієнт при х^k:

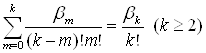
Приклад 1. Знайти .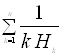

По 1.2.10 Н_k = ln k + O(1). Тоді

.

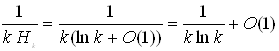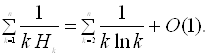
Застосуємо формулу підсумовування Ейлера:

.

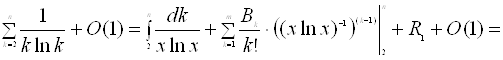
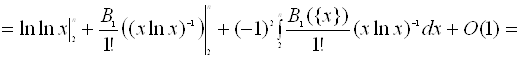
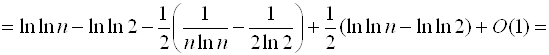
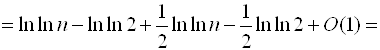
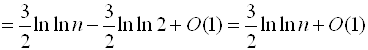Приклад 2. Знайти

Застосуємо формулу підсумовування Ейлера:

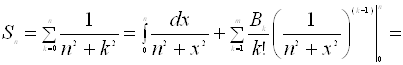
Приклад 3. Знайти асимптотику при n ® ¥ суми

Члени цієї суми швидко ростуть із ростом номера, так що головний член асимптотики дорівнює останньому члену суми: S(n) ~ n!, n ® ¥. Дійсно,

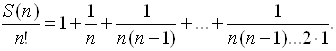
Отже,

Література

1. Брейн, Н.Г. Асимптотичні методи в аналізі. – К., 2006

2. Грехем, Р. Конкретна математика. Основи інформатики. – К.,2004

3. Олвер, Ф. Введення в асимптотичні методи й спеціальні функції. – К., 2004

4. Панченков, О.М. Асимптотичні методи в екстремальних задачах механіки. – К., 2004

5. Федорюк, М.В. Асимптотика: інтеграли й ряди. – К., 2005

6. Фихтенгольц, Г.М. Курс диференціального й інтегрального вирахування. – К., 2000