Навигация
Подання функцій рядів Фур'є
21220
знаков
0
таблиц
8
изображений
4. Подання функцій рядів Фур'є
Накладемо на функцію f(x) більше важка вимога, а саме-припустимо її у проміжку 
.
Тоді має місце загальна теорема:
Теорема. Якщо функція f(x) з періодом 
кусочно-диференцуєма в проміжку , то її ряд Фур'є в кожній крапці 
сходиться й має суму
Ця сума, мабуть, дорівнює 
, якщо в крапці функція безперервна.
Доказ. Відзначимо, що рівність (14) має місце для кожної функції f(x), що задовольняє поставленим умовам. Якщо, зокрема, взяти
, то 
, і з (14) одержимо, що
Множачи обидві частини рівності на постійне число 
й віднімаючи результат з (14), знайдемо
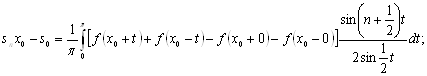
для нашої мети потрібно довести, що інтеграл праворуч при 
прагне до нуля.
Представимо його у вигляді
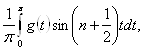(15)
де покладено
(16)
якби нам удалося встановити що ця функція кусочно-безперервна, то з леми попереднього параграфа варто було б уже, що інтеграл (15) має межу нулю при . Але в проміжку 
функція g(x) взагалі безперервна, за винятком хіба лише кінцевого числа крапок, де вона може мати перегони-тому що така функція f(x). Залишається відкритим лише питання про поводження функції g(x) при 
.
Ми доведемо існування кінцевої межі
;
поклавши тоді g(0)=K, ми в крапці t=0 одержимо безперервність, і застосування леми виявиться виправданим. Але другий множник у правій частині рівності (16) явно має межею одиницю; звернемося до вираження квадратних дужках.
Нехай, для простати, спочатку крапка 
лежить усередині проміжку, де функція f(x) диференцуєма. Тоді 
, і кожне зі співвідношень
(17)
прагне до межі 
, а 
— до нуля. Якщо ж є "крапка стику", то при цьому вона може виявитися як крапкою безперервності, так і крапкою розриву. У першому випадку ми знову зштовхнемося з відношенням (17), але вони будуть прагнути цього разу до різних меж, відповідно-до похідній праворуч і до похідної ліворуч. До аналогічного результату прийдемо й у випадку розриву, але тут заміниться значеннями 
тих функцій, від склеювання яких вийшла дана, а межами відносин (17) будуть однобічні похідні згаданих функцій при .
Отже, наш висновок справедливо у всіх випадках.
5. Випадок неперіодичної функції
Вся побудована вище теорія виходила із припущення, що задана функція визначена для всіх речовинних значень x і притім має період . Тим часом найчастіше доводиться мати справа з неперіодичною функцією f(x), інший раз навіть заданої тільки в проміжку 
.
Що б мати право застосувати до такої функції викладену теорію, уведемо замість її допоміжну функцію 
певну в такий спосіб. У проміжку 
ми ототожнюємо 
з f(x):
(18)
потім думаємо
а на інші речовинні значення x поширюємо функцію за законом періодичності.
До побудованого в такий спосіб функції з періодом можна вже застосувати доведену теорему розкладання. Однак, якщо мова йде про крапку , що строго лежить між 
і 
, те, через (18), нас довелося б мати справа із заданою функцією 
. По тій же причині й коефіцієнти розкладання можна обчислити по формулах обчислення коефіцієнтів не переходячи до допоміжної функції. Коротше кажучи, все доведене вище безпосередньо переноситься на задану функцію , минаючи допоміжну функцію .
Особливої уваги, однак, вимагають кінці проміжку 
. При застосуванні до функції теореми попереднього параграфа, скажемо, у крапці 
, нам довелося б мати справа як зі значеннями допоміжної функції праворуч від , де вони збігаються вже зі значеннями праворуч від 
ю Тому для як значення 
належало б взяти
.
Таким чином, якщо задана функція навіть безперервна при , але не має періоду , так що 
, те-при дотриманні вимог сумою ряду Фур'є буде число
відмінне як від 
, так і від 
. Для такої функції розкладання має місце лише у відкритому проміжку 
.
Наступне зауваження так само заслуговує на особливу увагу. Якщо тригонометричний ряд
сходиться в проміжку 
до функції , то через те, що його члени мають період , він сходиться всюди, і сума його 
теж виявляється періодичною функцією з періодом . Але ця сума поза зазначеним проміжком взагалі вже не збігається з функцією .
Похожие работы
... що найбільший теоретичний і прикладний інтерес представляє випадок викладений у другому розділі. Розділ 2 Всі результати першого розділу, що стосуються дзета-функції Римана, були отримані в припущенні, що її аргумент s – дійсне число. Однак, найвидатніші дослідження й численні важливі додатки стали можливі лише після включення в область визначення функції комплексних чисел. Уперше розглянув ...
... общин, де кожний буде зобов'язаний трудитися. М.А. Бакунін дотримувався ідей анархізму, бачивши у владі причину експлуатації. Один з феноменів російської науки - плідна розробка ідей економіко-математичного моделювання, заснована на базі як „чистих” математиків, що направили свої зусилля в економіку, так і розробок професійних економістів. Перші російські економісти-математики (Ю.Г. Жуковській, ...
... усю країну. Незважаючи на те, що твори соціалістів-утопістів не мали серйозної теоретичної основи, вони відобразили пошуки ідеального справедливого суспільства та справили значний вплив на еволюцію економічної думки. Видатні мислителі-утопісти: започаткували глибоку критику існуючого суспільного ладу, його суперечностей і спонукали до роздумів над проблемами еволюції людського суспільства; ...
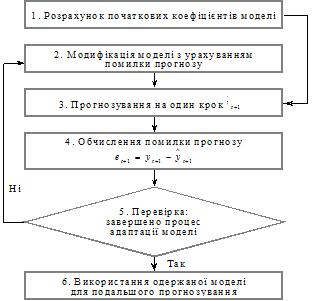
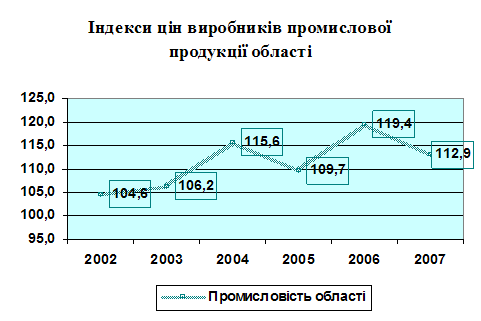
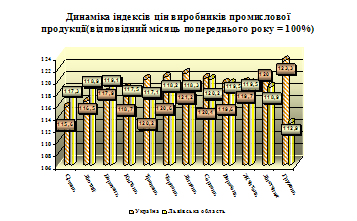
... ікативна модель дає неточні результати. У процесі побудови моделі виконують числову оптимізацію параметрів адаптації в межах [0; 1]. РОЗДІЛ 3 СТАТИСТИЧНА ОЦІНКА ТА ПРОГНОЗУВАННЯ ЦІН НА ПРОМИСЛОВУ ПРОДУКЦІЮ У ЛЬВІВСЬКІЙ ОБЛАСТІ 3.1 Статистичний аналіз цін виробників промислової продукції у Львівській області У Львівській області індекс цін виробників промислової продукції у 2007 році ...
0 комментариев