Навигация
Випадок довільного проміжку
6. Випадок довільного проміжку
Припустимо, що функція ![]() задана в проміжку
задана в проміжку ![]() довільної довжини
довільної довжини ![]() в ньому. Якщо вдатися до підстановки
в ньому. Якщо вдатися до підстановки
![]() ,
,
те вийде функція ![]() від
від ![]() у проміжку
у проміжку ![]() , теж кусочно-диференцуєма, до якої вже прикладемо розгляду попереднього параграфа. Як ми бачили, за винятком крапок розриву й кінців проміжку, можна розкласти її в ряд Фур'є:
, теж кусочно-диференцуєма, до якої вже прикладемо розгляду попереднього параграфа. Як ми бачили, за винятком крапок розриву й кінців проміжку, можна розкласти її в ряд Фур'є:
![]()
коефіцієнти якого визначаються формулами Ейлера-Фур'є:
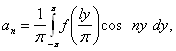
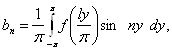
![]()
![]()
повернемося тепер до колишньої змінного ![]() , думаючи
, думаючи
![]() .
.
Тоді одержимо розкладання заданої функції ![]() в тригонометричний ряд трохи зміненого виду:
в тригонометричний ряд трохи зміненого виду:
![]() (19)
(19)
Тут косинуси й синуси беруться від кутів, кратних не ![]() , а
, а ![]() . Можна було б і формули для визначення коефіцієнтів розкладання перетворити тією же підстановкою до виду
. Можна було б і формули для визначення коефіцієнтів розкладання перетворити тією же підстановкою до виду
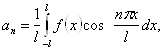
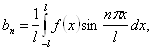 (20)
(20)
![]()
![]()
Відносно кінців проміжку ![]() зберігають силу зауваження, зроблені в попередньому параграфі щодо крапок
зберігають силу зауваження, зроблені в попередньому параграфі щодо крапок ![]() Звичайно, проміжок
Звичайно, проміжок ![]() може бути замінений будь-яким іншим проміжком довгі
може бути замінений будь-яким іншим проміжком довгі ![]() зокрема, проміжком
зокрема, проміжком ![]() . В останньому випадку формули (20) повинні бути замінені формулами
. В останньому випадку формули (20) повинні бути замінені формулами
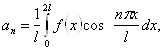
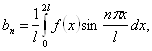 (20a)
(20a)
![]()
![]()
7. Випадок парних і непарних функцій
Якщо задана в проміжку ![]() функція
функція ![]() буде непарної, то очевидно
буде непарної, то очевидно
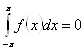
У цьому легко переконається:
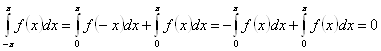 .
.
Таким же шляхом установлюється, що у випадку парної функції ![]() :
:
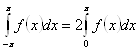 .
.
Нехай тепер ![]() буде кусочно-диференцуєма в проміжку
буде кусочно-диференцуєма в проміжку ![]() парна функція. Тоді добуток
парна функція. Тоді добуток ![]() виявиться непарною функцією, і по сказаному
виявиться непарною функцією, і по сказаному
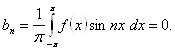
Таким чином, ряд Фур'є парної функції містить одні лише косинусів:
![]() (21)
(21)
Тому що ![]() в цьому випадку буде теж парною функцією, те, застосувавши сюди друге зі зроблених вище зауважень, можемо коефіцієнти
в цьому випадку буде теж парною функцією, те, застосувавши сюди друге зі зроблених вище зауважень, можемо коефіцієнти ![]() розкладання написати у вигляді
розкладання написати у вигляді
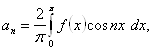
![]() (22)
(22)
Якщо ж функція ![]() буде непарної, то непарної буде й функція
буде непарної, то непарної буде й функція ![]() , так що
, так що
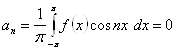
![]()
Ми доходимо висновку, що ряд Фур'є непарної функції містить одні лише синусів:
![]() (23)
(23)
При цьому через парність добутку ![]() можна писати:
можна писати:
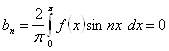
![]() (24)
(24)
Відзначимо, що кожна функція ![]() , задана в проміжку
, задана в проміжку ![]() , може бути представлена у вигляді суми парних і непарної тридцятимільйонних функцій:
, може бути представлена у вигляді суми парних і непарної тридцятимільйонних функцій:
![]() ,
,
Де
![]()
Очевидно, що ряд Фур'є функції ![]() саме й складеться з розкладання по косинусах функції
саме й складеться з розкладання по косинусах функції ![]() й розкладання по синусах функції
й розкладання по синусах функції ![]() .
.
Припустимо, далі, що функція ![]() задана лише в проміжку
задана лише в проміжку ![]() . Бажаючи розкласти її в цьому проміжку в ряд Фур'є ми доповнимо визначення нашої функції для значень x у проміжку
. Бажаючи розкласти її в цьому проміжку в ряд Фур'є ми доповнимо визначення нашої функції для значень x у проміжку ![]() по сваволі, а потім застосуємо сказане в пункті "Випадок неперіодичної функції".
по сваволі, а потім застосуємо сказане в пункті "Випадок неперіодичної функції".
Можна використовувати сваволю у визначенні функції в проміжку ![]() так, що б одержати для
так, що б одержати для ![]() розкладання тільки лише по косинусах або тільки по синусах. Дійсно, представимо семі, що для
розкладання тільки лише по косинусах або тільки по синусах. Дійсно, представимо семі, що для ![]() ми думаємо
ми думаємо ![]() , так що в результаті виходить парна функція в проміжку
, так що в результаті виходить парна функція в проміжку ![]() . Її розкладання, як ми бачили, буде містити одні лише косинуси. Коефіцієнти розкладання можна обчислювати по формулах (22), куди входять лише значення спочатку заданої функції
. Її розкладання, як ми бачили, буде містити одні лише косинуси. Коефіцієнти розкладання можна обчислювати по формулах (22), куди входять лише значення спочатку заданої функції ![]() .
.
Аналогічно, якщо доповнити визначення функції ![]() за законом непарності, то вона стане непарної й у її розкладанні будуть одні лише синуси. Коефіцієнти її розкладання визначаються по формулах (24).
за законом непарності, то вона стане непарної й у її розкладанні будуть одні лише синуси. Коефіцієнти її розкладання визначаються по формулах (24).
Таким чином, задану в проміжку ![]() функцію при дотриманні умов виявляється можливим розкладати як по косинусах, так і по одним лише синусах.
функцію при дотриманні умов виявляється можливим розкладати як по косинусах, так і по одним лише синусах.
Особливого дослідження вимагають крапки ![]() й
й ![]() . Тут обоє розкладання поводяться по-різному. Припустимо, для простоти, що задана функція
. Тут обоє розкладання поводяться по-різному. Припустимо, для простоти, що задана функція ![]() безперервна при
безперервна при ![]() й
й ![]() , і розглянемо спочатку розкладання по косинусах. Умова
, і розглянемо спочатку розкладання по косинусах. Умова ![]() , насамперед, зберігає безперервність при
, насамперед, зберігає безперервність при ![]() , так що ряд (21) при
, так що ряд (21) при ![]() буде сходитися саме к.
буде сходитися саме к.![]() Тому що, далі,
Тому що, далі,
![]()
те й при ![]() має помста аналогічна обставина.
має помста аналогічна обставина.
Інакше є справа з розкладанням по синусах. У крапках ![]() і
і ![]() сума ряду (23) явно буде нулем. Тому вона може дати нам значення
сума ряду (23) явно буде нулем. Тому вона може дати нам значення ![]() й
й![]() , мабуть, лише в тому випадку, якщо ці значення дорівнюють нулю.
, мабуть, лише в тому випадку, якщо ці значення дорівнюють нулю.
Якщо функція ![]() задана в проміжку
задана в проміжку ![]() те, удавшись до тієї ж заміни змінної, що й у попередньому параграфі, ми зведемо питання про розкладання її в ряд по косинусах
те, удавшись до тієї ж заміни змінної, що й у попередньому параграфі, ми зведемо питання про розкладання її в ряд по косинусах
![]()
або в ряд по синусах
![]()
до тільки що розглянутого. При цьому коефіцієнти розкладань обчислюються, відповідно, по формулах
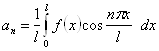
![]()
або
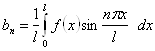
![]() .
.
Похожие работы
... що найбільший теоретичний і прикладний інтерес представляє випадок викладений у другому розділі. Розділ 2 Всі результати першого розділу, що стосуються дзета-функції Римана, були отримані в припущенні, що її аргумент s – дійсне число. Однак, найвидатніші дослідження й численні важливі додатки стали можливі лише після включення в область визначення функції комплексних чисел. Уперше розглянув ...
... общин, де кожний буде зобов'язаний трудитися. М.А. Бакунін дотримувався ідей анархізму, бачивши у владі причину експлуатації. Один з феноменів російської науки - плідна розробка ідей економіко-математичного моделювання, заснована на базі як „чистих” математиків, що направили свої зусилля в економіку, так і розробок професійних економістів. Перші російські економісти-математики (Ю.Г. Жуковській, ...
... усю країну. Незважаючи на те, що твори соціалістів-утопістів не мали серйозної теоретичної основи, вони відобразили пошуки ідеального справедливого суспільства та справили значний вплив на еволюцію економічної думки. Видатні мислителі-утопісти: започаткували глибоку критику існуючого суспільного ладу, його суперечностей і спонукали до роздумів над проблемами еволюції людського суспільства; ...
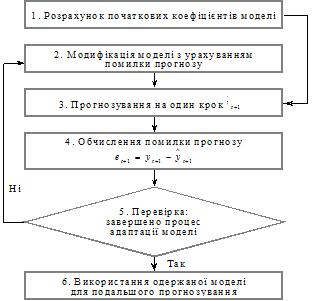
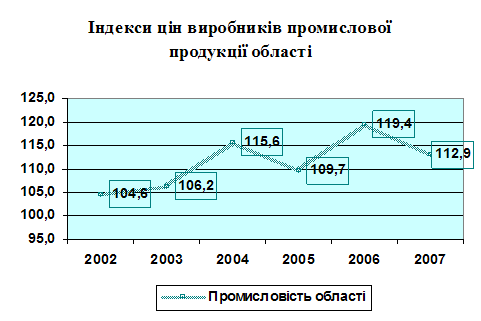
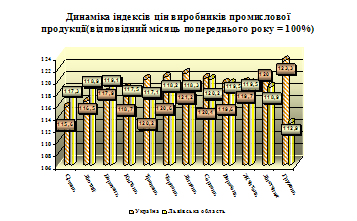
... ікативна модель дає неточні результати. У процесі побудови моделі виконують числову оптимізацію параметрів адаптації в межах [0; 1]. РОЗДІЛ 3 СТАТИСТИЧНА ОЦІНКА ТА ПРОГНОЗУВАННЯ ЦІН НА ПРОМИСЛОВУ ПРОДУКЦІЮ У ЛЬВІВСЬКІЙ ОБЛАСТІ 3.1 Статистичний аналіз цін виробників промислової продукції у Львівській області У Львівській області індекс цін виробників промислової продукції у 2007 році ...

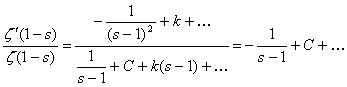
0 комментариев