Навигация
Приклади розкладання функцій у ряд Фур'є
8. Приклади розкладання функцій у ряд Фур'є
Функції, які нижче приводяться як приклади, як правило, ставляться до класу диференцуємих або кусочно-диференцуємих. Тому сама можливість їхнього розкладання в ряд Фур'є-Поза сумнівом, і на цьому ми зупинятися не будемо.
Всі завдання взяті зі Збірника задач і вправ по математичному аналізі, Б. Н. Демидович.
№ 2636. Функцію ![]() розкласти в ряд Фур'є.
розкласти в ряд Фур'є.
Тому що функція ![]() є непарної, те, отже,
є непарної, те, отже, ![]() буде парною. Тому її розкладання в ряд Фур'є містить одні лише косинусів.
буде парною. Тому її розкладання в ряд Фур'є містить одні лише косинусів.
Знайдемо коефіцієнти розкладання;

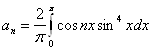
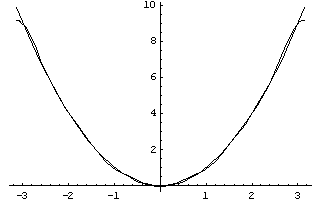
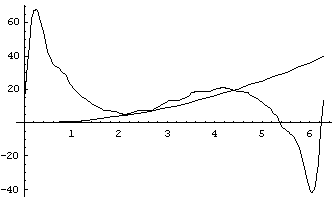
№ 2938. Розкласти в ряд Фур'є функцію ![]() . Зобразити цієї функції й графіки декількох приватних сум ряду Фур'є цієї функції.
. Зобразити цієї функції й графіки декількох приватних сум ряду Фур'є цієї функції.
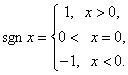
Функція ![]() непарна, тому її розкладання буде містити одні лише синуси.
непарна, тому її розкладання буде містити одні лише синуси.
![]()
Тобто, виходить, що при парних значеннях n коефіцієнт ![]() , а отже й весь доданок, звертається в нуль. Тому підсумовування йде тільки лише за парним значенням n.
, а отже й весь доданок, звертається в нуль. Тому підсумовування йде тільки лише за парним значенням n.
Ряд Фур'є для цієї функції прийме наступний вид:
![]() .
. ![]()
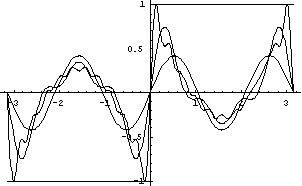
Нижче зображені графіки функцій ![]() і декількох часток сум ряду Фур'є:
і декількох часток сум ряду Фур'є:
Графік функції ![]() ,
, ![]() ,
, ![]() і
і ![]()
№ 2940. ![]() в інтервалі
в інтервалі ![]() .
.
Функція![]() непарна.
непарна.
![]()
![]()
№ 2941. ![]() в інтервалі
в інтервалі ![]() .
.
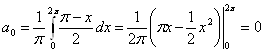

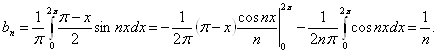
У підсумку одержуємо ряд Фур'є:
![]()
![]()
№ 2941. ![]() в інтервалі
в інтервалі ![]() .
.
Функція ![]() парна.
парна.
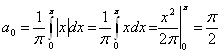
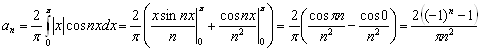
Як і в № 2938, у нас при парних значеннях n коефіцієнт ![]() звертається в нуль. Тому підсумувати будемо лише за непарним значенням.
звертається в нуль. Тому підсумувати будемо лише за непарним значенням.
У підсумку одержимо:
![]()
№ 2950. ![]() в інтервалі
в інтервалі ![]() .
.
Функція ![]() парна.
парна.
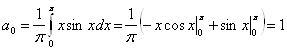
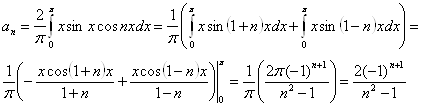
Тому що при n=1 знаменник звертається в нуль, то підсумовування необхідно зробити починаючи у двійки.
![]()
№ 2951. ![]() в інтервалі
в інтервалі ![]() .
.
Функція ![]() непарна.
непарна.
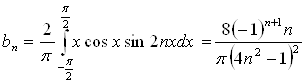
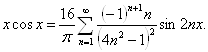
№ 2961. Функцію ![]() розкласти а) в інтервалі
розкласти а) в інтервалі ![]() по косинусах кратних дуг; б) в інтервалі
по косинусах кратних дуг; б) в інтервалі ![]() по синусах кратних дуг; в) в інтервалі
по синусах кратних дуг; в) в інтервалі ![]() . Зобразити графік функції
. Зобразити графік функції ![]() й сум рядів Фур'є для кожного окремого випадку. Використовуючи розкладання, знайти суми рядів:
й сум рядів Фур'є для кожного окремого випадку. Використовуючи розкладання, знайти суми рядів: ![]() ;
; ![]() і
і ![]() .
.
а) 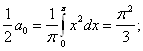
![]()
І, нарешті одержуємо розкладання в ряд Фур'є:
![]()
![]()
б) ![]()
![]()
![]()
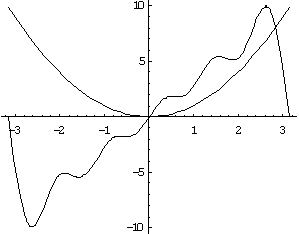
в) 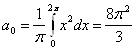
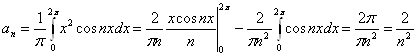
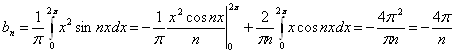
![]()
![]()
№ 2962 Виходячи з розкладання
![]()
![]() ,
,
По членним інтегруванням одержати розкладання в ряд Фур'є на інтервалі ![]() функцій
функцій ![]()
інтегруємо рівність ![]() по членне, одержимо
по членне, одержимо
![]()
І остаточно одержуємо:
![]()
![]()
Інтегруємо отриману рівність повторно
![]()
або звідси одержуємо
![]() .
.
Список літератури
1.І.М. Уваренков, М.З. Маллер Курс математичного аналізу., - К., 2006
2.Г.М. Фихтенгольц Курс диференціального й інтегрального вирахування. – К., 2005р.
3.В.Е. Шнейдер, А.И. Слуцкий, А.С. Шумов Курс вищої математики. – К., 2005
4.Н.Я. Виленкин, В.В. Цукерман, М.А. Доброхотова, А.Н. Сафонов Ряди. – К., 1997
5.Б.П. Демидович Збірник задач і вправ по математичному аналізу. – К., 2005
Похожие работы
... що найбільший теоретичний і прикладний інтерес представляє випадок викладений у другому розділі. Розділ 2 Всі результати першого розділу, що стосуються дзета-функції Римана, були отримані в припущенні, що її аргумент s – дійсне число. Однак, найвидатніші дослідження й численні важливі додатки стали можливі лише після включення в область визначення функції комплексних чисел. Уперше розглянув ...
... общин, де кожний буде зобов'язаний трудитися. М.А. Бакунін дотримувався ідей анархізму, бачивши у владі причину експлуатації. Один з феноменів російської науки - плідна розробка ідей економіко-математичного моделювання, заснована на базі як „чистих” математиків, що направили свої зусилля в економіку, так і розробок професійних економістів. Перші російські економісти-математики (Ю.Г. Жуковській, ...
... усю країну. Незважаючи на те, що твори соціалістів-утопістів не мали серйозної теоретичної основи, вони відобразили пошуки ідеального справедливого суспільства та справили значний вплив на еволюцію економічної думки. Видатні мислителі-утопісти: започаткували глибоку критику існуючого суспільного ладу, його суперечностей і спонукали до роздумів над проблемами еволюції людського суспільства; ...
... ікативна модель дає неточні результати. У процесі побудови моделі виконують числову оптимізацію параметрів адаптації в межах [0; 1]. РОЗДІЛ 3 СТАТИСТИЧНА ОЦІНКА ТА ПРОГНОЗУВАННЯ ЦІН НА ПРОМИСЛОВУ ПРОДУКЦІЮ У ЛЬВІВСЬКІЙ ОБЛАСТІ 3.1 Статистичний аналіз цін виробників промислової продукції у Львівській області У Львівській області індекс цін виробників промислової продукції у 2007 році ...

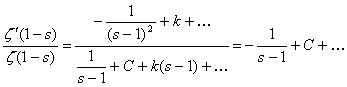
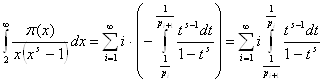
0 комментариев