Навигация
ПОСТРОЕНИЕ НЕНОРМАЛИЗОВАННОГО U-ГРАФА КОСВЕННЫМ МЕТОДОМ
3 ПОСТРОЕНИЕ НЕНОРМАЛИЗОВАННОГО U-ГРАФА КОСВЕННЫМ МЕТОДОМ
Представим исходную схему в каноническом виде. Параметры этой схемы (рисунок 3.1) равны
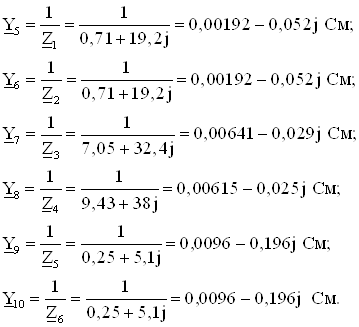
Заменим все источники Э.Д.С. на источники тока
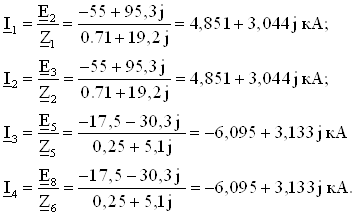
Система уравнений для U-графа, описывающих энергетическое состояние цепи, имеет следующий вид
![]()
где Y–квадратная матрица проводимостей; U–это матрицы-столбцы неизвестных узловых напряжений; Iуз – это матрица-столбец узловых токов.
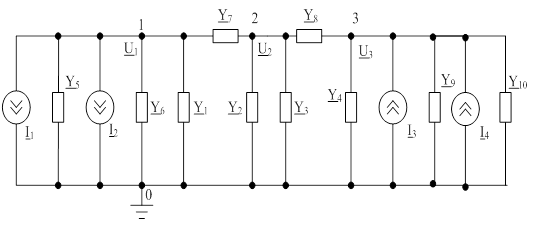
Рисунок 3.1 – Мнемосхема электрической цепи для построения U–графа
Составим матрицу-столбец узловых напряжений U
 .
.
Матрица-столбец узловых токов Iуз будет иметь вид

Матрица взаимных проводимостей
 ,
,
Найдем значения элементов матрицы

Подставляя значения проводимостей в исходную матрицу, получим следующую формулу
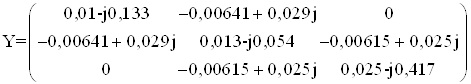 .
.
При построении по системе уравнений ненормализованного U-графа необходимо пользоваться только нормированными (безразмерными) величинами. Поэтому вводим масштабные множители
Y0=1, См; U0= 1, В; I0 = 1, А;
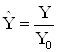 ;
;  ;
; ![]() .
.
Составим ненормализованную матрицу передач А

где n – порядок матрицы ![]() , n = 3; m – количество ненулевых элементов матрицы
, n = 3; m – количество ненулевых элементов матрицы ![]() , m=2; 1n – единичная матрица порядка n; -1m – отрицательная единичная матрица порядка m; 0(n-m)m – нулевая матрица, состоящая из (n-m) строк и m столбцов.
, m=2; 1n – единичная матрица порядка n; -1m – отрицательная единичная матрица порядка m; 0(n-m)m – нулевая матрица, состоящая из (n-m) строк и m столбцов.
Опираясь на предыдущие уравнения строим ненормализованную матрицу передач

Подставим числовые значения
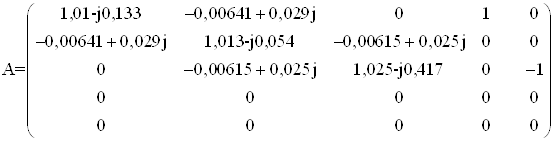 .
.
На основании этой матрицы передач строим ненормализованный U–граф (рисунок 3.2). Так как у данного графа узлы-источники не соответствуют источникам в исходной схеме, преобразуем его, разделив узлы-источники (рисунок 3.3).
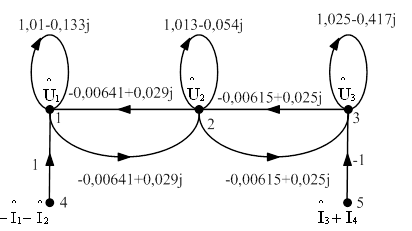
Рисунок 3.2 – Ненормализованный U – граф без преобразованных источников
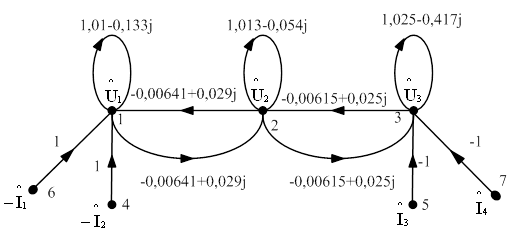
Рисунок 3.3 – Ненормализованный U
4 ПРЕОБРАЗОВАНИЕ НЕНОРМАЛИЗОВАННОГО U-ГРАФА В НОРМАЛИЗОВАННЫЙ U-ГРАФ
Преобразуем полученный U-граф в нормализованный (рисунок 4.1). C этой целью исключим петли из ненормализованного графа. Тогда по правилам преобразования графов передачи нормализованного U-графа будут иметь следующие значения
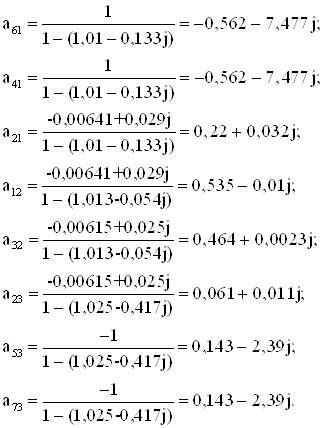
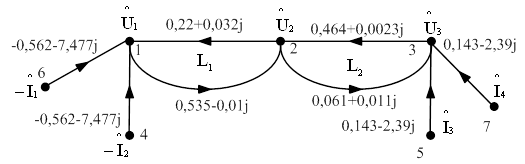
Рисунок 4.1 – Нормализованный U – граф
5 РАСЧЕТ УЗЛОВОГО НАПРЯЖЕНИЯ В ЗАВИСИМОМ УЗЛЕ НЕНОРМАЛИЗОВАННОГО И НОРМАЛИЗОВАННОГО U-ГРАФАХ НА ОСНОВАНИИ ФОРМУЛЫ МЭЗОНА
Для начала рассчитаем напряжения в узлах ненормализованного графа (рисунок 3.3). Запишем все контуры этого графа
L1=a11=1,01-0,133j;
L2=a22=1,013-0,054j;
L3=a33=1,025-0,417j;
L4=a12∙ a21=(-0,00641+0,029j)2=-0,0008-0,000372j;
L5=a23∙ a32=(-0,00615+0,025j)2=-0,00059-0,0003075j.
Рассчитаем напряжение в 1 узле ненормализованного графа. Формула Мэзона для этого случая имеет вид
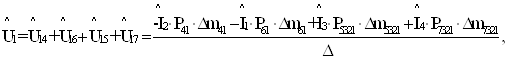 (5.1)
(5.1)
где Р61 - путь от узла 6 к узлу 1; Р41 - путь от узла 4 к узлу 1; Р5321 - путь от узла 5 к узлу 1; Р7321 - путь от узла 7 к узлу 1 Δm61 - алгебраическое дополнение пути от узла 6 к узлу 1; Δm41 - алгебраическое дополнение пути от узла 4 к узлу 1; Δm5321 - алгебраическое дополнение пути от узла 5 к узлу 1; Δm7321 - алгебраическое дополнение пути от узла 7 к узлу 1 ![]() - определитель графа.
- определитель графа.
Δ=1 - (L1+L2+L3+L4+L5) + (L1![]() L2+L1
L2+L1![]() L3+L3·L2+L1·L5+L3·L4) - (L1·L2·L3) =
L3+L3·L2+L1·L5+L3·L4) - (L1·L2·L3) =
= 1 - (1,01 - 0,133j + 1,013 - 0,054j + 1,025 - 0,417j - 0,0008 - 0,000372j - 0,00059 -
- 0,0003075j) + ((1,01 - 0,133j)·(1,013 - 0,054j) + (1,01 - 0,133j)·(1,025 - 0,417j) +
+ (1,025 - 0,417j) · (1,013 - 0,054j) + (1,01-0,133j) · (-0,00059-0,0003075j)+(1,025-
- 0,417j) · (- 0,0008 - 0,000372j) - (1,01 - 0,133j) · (1,013 - 0,054j) · (1,025-0,417j) = =0,0009-0,00248j
Δm61=1-(L5+L2+L3)+L3·L2=1-(-0,00059-0,0003075j +1,013-0,054j +1,025-
-0,417j) + (1,025-0,417j)·( 1,013-0,054j)=-0,022-0,00646j;
Δm41=1-(L5+L2+L3)+L3·L2=1-(-0,00059-0,0003075j +1,013-0,054j +1,025-
-0,417j) + (1,025-0,417j)·( 1,013-0,054j)=-0,022-0,00646j;
Δm5321=1;
Δm7321=1;
P61= 1;
P41= 1;
P5321=a53·a32·a21=-1∙(-0,00615+0,025j)∙(-0,00641+0,029j)=0,000686+0,00034j.
P5321= P7321
Подставляя найденные значения в формулу Мэзона (5.1) получим
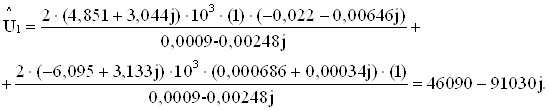
Чтобы получить размерную величину напряжения умножим полученное значение на масштабный множитель
![]() .
.
Рассчитаем напряжение в первом узле нормализованного графа, изображенного на рисунке 4.1. Для этого воспользуемся той же формулой Мэзона, что и для ненормализованного графа, только изменим все входящие в нее элементы. В нормализованном графе имеем всего два некасающихся контура
L1= a12∙ a21=(0,22+0,032j)·(0,535-0,01j)=0,118+0,015j;
L2= a23∙ a32=(0,464+0,0023j)·(0,061+0,011j)=0,028+0,00065j.
Тогда находим оставшиеся члены формулы
Δн=1- (L1+L2)=1- (0,118+0,015j + 0,028+0,00065j) =0,854-0,016j;
P5321н=a53·a32·a21=(0,143-2,39j)∙(0,464+0,0023j)·(0,22+0,032j)=
= 0,051-0,242j.
Алгебраические дополнения путей вычисляются следующим образом
Δm41н=1- (L2)=1-0,028-0,00065j =0,972-0,00065j;
Δm61н=1- (L2)= 1-0,028-0,00065j =0,972-0,00065j;
Δm5321н=1;
Δm7321н=1.
Вычисляем напряжение в первом узле по формулам (5.1), приведенным выше
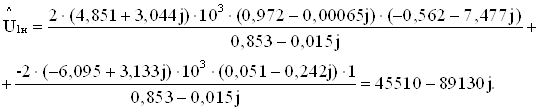
![]() .
.
Погрешность равна
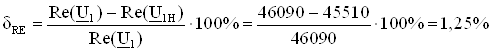 ;
;
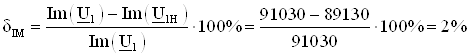 .
.
Как видим, погрешности меньше 5%, следовательно, расчеты верны. Напряжение в узлах, найденное с использованием формулы Мэзона, получилось одинаковым для ненормализованного и нормализованного графа, следовательно, эти графы равносильны.
6 ПОСТРОЕНИЕ НЕНОРМАЛИЗОВАННОГО U-ГРАФА ПРЯМЫМ МЕТОДОМ
Алгоритм построения U-графа прямым методом следующий:
1. На поле графа наносим узлы, которые соответствуют неизвестным напряжениям в узлах схемы;
2. Каждую пару узлов соединяем двумя противоположно направленными ветвями с передачами равными взаимным проводимостям между узлами схемы и помноженными на -1;
3. Строим в узлах графа петли с передачами равными сумме проводимостей всех ветвей, сходящихся в данном узле и прибавляем к ним единицу;
4. Наносим на поле графа узлы-источники и соединяем их с зависимыми узлами передачами равными -1, если ток подтекает к узлу, и +1, в противоположном случае.
Пользуемся схемой, представленной в каноническом виде (рисунок 3.1). В результате получаем граф, изображенный на рисунке 6.1. Находим значения проводимостей

В результате получили ненормализованный граф, изображенный на рисунке 6.2. Ненормализованные U-графы, построенные прямым и косвенным методом, получились одинаковыми, что говорит об их равносильности.
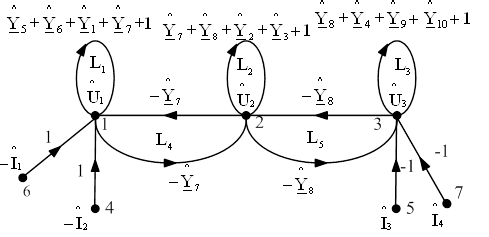
Рисунок 6.1 – Ненормализованный U–граф, построенный прямым методом

Рисунок 6.2 – Ненормализованный U–граф, построенный прямым методом
ЗАКЛЮЧЕНИЕ
В данной работе было проведено исследование дифференциально-интегральных уравнений. В результате были получены критерии подобия способами интегральных аналогов и на базе π-теоремы. Анализируя эти методы можно сделать выводы, что исследование методом интегральных аналогов является менее объемным, в сравнении с исследованием на базе π-теоремы, но дает меньшее число форм записи критериев подобия.
Также мы ознакомились с теорией графов. Теория графов позволяет вскрывать внутренние причинно следственные связи между параметрами процесса и системы. Благодаря этому аппарат теории графов адекватен природе изучаемых явлений. В силу чего теория графов не ограничивается анализом электрических систем и находит применение в различных областях техники. Выполнено построение для электрической схемы косвенным методом ненормализованного U-графа с дальнейшим его преобразованием в нормализованный. При помощи формулы Мэзона было рассчитано узловое напряжение в зависимом узле этого графа. Выяснено, что узловые напряжения имеют одинаковые значения для ненормализованного и нормализованного U-графов.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. Бойчевский, В. И. Методические указания и контрольные задания к курсовой работе «Применение методов моделирования к электротехническим задачам» по дисциплине «Моделирование в технике» (для студентов специальности 140610) [Текст]: / В. И. Бойчевский, А. Н. Шпиганович. – Липецк: ЛГТУ, 2009. – 22с.
2. Бугров, Я. С. Высшая математика. Элементы линейной алгебры и аналитической геометрии [Текст]: / Я. С. Бугров, С. М. Никольский. – Ростов: Феникс, 1997. – 288с.
3. Шпиганович, А. Н. Методические указания к оформлению учебно-технической документации [Текст] / А. Н. Шпиганович, В. И. Бойчевский. – Липецк: ЛГТУ, 1997. – 32с.
ПРИЛОЖЕНИЕ
Расчет определителей третьего порядка
| L | M | T | L | M | I | L | T | I | M | T | I | |||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | C1 | -2 | 4 | 2 | = | 0 | L1 | 1 | -2 | -2 | = | -1 | |||
| i1 | 0 | 0 | 0 | i1 | 0 | 0 | 1 | L2 | 2 | -2 | -2 | i1 | 0 | 0 | 1 | |||||||||||
| t | 0 | 0 | 1 | t | 0 | 0 | 0 | R2 | 2 | -3 | -2 | t | 0 | 1 | 0 | |||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I | |||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | t | 0 | 1 | 0 | = | 0 | L1 | 1 | -2 | -2 | = | -2 | |||
| i1 | 0 | 0 | 0 | i1 | 0 | 0 | 1 | R1 | 2 | -3 | -2 | i1 | 0 | 0 | 1 | |||||||||||
| C1 | -2 | -1 | 4 | C1 | -2 | -1 | 2 | R2 | 2 | -3 | -2 | C1 | -1 | 4 | 2 | |||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I | |||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | t | 0 | 1 | 0 | = | 0 | L1 | 1 | -2 | -2 | = | 1 | |||
| i1 | 0 | 0 | 0 | i1 | 0 | 0 | 1 | L2 | 2 | -2 | -2 | i1 | 0 | 0 | 1 | |||||||||||
| R1 | 2 | 1 | -3 | R1 | 2 | 1 | -2 | R2 | 2 | -3 | -2 | R1 | 1 | -3 | -2 | |||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I | |||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | C | -2 | 4 | 2 | = | 0 | L1 | 1 | -2 | -2 | = | 0 | |||
| i1 | 0 | 0 | 0 | i1 | 0 | 0 | 1 | R1 | 2 | -3 | -2 | i1 | 0 | 0 | 1 | |||||||||||
| i2 | 0 | 0 | 0 | i2 | 0 | 0 | 1 | L2 | 2 | -2 | -2 | i2 | 0 | 0 | 1 | |||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I | |||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | t | 0 | 1 | 0 | = | 0 | L1 | 1 | -2 | -2 | = | 0 | |||
| i1 | 0 | 0 | 0 | i1 | 0 | 0 | 1 | C | -2 | 4 | 2 | i1 | 0 | 0 | 1 | |||||||||||
| L2 | 2 | 1 | -2 | L2 | 2 | 1 | -2 | R1 | 2 | -3 | -2 | L2 | 1 | -2 | -2 | |||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I | |||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | L2 | 2 | -2 | -2 | = | 0 | L1 | 1 | -2 | -2 | = | 1 | |||
| i1 | 0 | 0 | 0 | I1 | 0 | 0 | 1 | C | -2 | 4 | 2 | i1 | 0 | 0 | 1 | |||||||||||
| R2 | 2 | 1 | -3 | R2 | 2 | 1 | -2 | t | 0 | 1 | 0 | R2 | 1 | -3 | -2 | |||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I | |||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | C | -2 | 4 | 2 | = | 0 | L1 | 1 | -2 | -1 | = | 0 | |||
| t | 0 | 0 | 1 | t | 0 | 0 | 0 | t | 0 | 1 | 0 | C1 | -1 | 4 | 2 | |||||||||||
| C1 | -2 | -1 | 4 | C1 | -2 | -1 | 2 | R2 | 2 | -3 | -2 | t | 0 | 1 | 0 | |||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I | |||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | R1 | 2 | -3 | -2 | = | 0 | L1 | 1 | -2 | -2 | = | 0 | |||
| t | 0 | 0 | 1 | t | 0 | 0 | 0 | t | 0 | 1 | 0 | R1 | 1 | -3 | -2 | |||||||||||
| R1 | 2 | 1 | -3 | R1 | 2 | 1 | -2 | L2 | 2 | -2 | -2 | t | 0 | 1 | 0 | |||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | L2 | 2 | -2 | -2 | = | 0 | L1 | 1 | -2 | -2 | = |
| |||
| t | 0 | 0 | 1 | t | 0 | 0 | 0 | R2 | 2 | -3 | -2 | t | 0 | 1 | 0 |
| ||||||||||
| I2 | 0 | 0 | 0 | i2 | 0 | 0 | 1 | L1 | 2 | -2 | -2 | i2 | 0 | 0 | 1 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | -2 | -2 | = | -2 | L1 | 1 | -2 | -2 | = |
| |||
| t | 0 | 0 | 1 | t | 0 | 0 | 0 | i1 | 0 | 0 | 1 | L2 | 1 | -2 | -2 |
| ||||||||||
| L2 | 2 | 1 | -2 | L2 | 2 | 1 | -2 | t | 0 | 1 | 0 | t | 0 | 1 | 0 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | -2 | -2 | = | -4 | L1 | 1 | -2 | -2 | = |
| |||
| R2 | 2 | 1 | -3 | R2 | 2 | 1 | -2 | i1 | 0 | 0 | 1 | t | 0 | 1 | 0 |
| ||||||||||
| t | 0 | 0 | 1 | t | 0 | 0 | 0 | C1 | -2 | 4 | 2 | R2 | 1 | -3 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | -2 | -2 | = | 2 | L1 | 1 | -2 | -2 | = |
| |||
| C1 | -2 | -1 | 4 | C1 | -2 | -1 | 2 | R1 | 2 | -3 | -2 | R1 | 1 | -3 | -2 |
| ||||||||||
| R1 | 2 | 1 | -3 | R1 | 2 | 1 | -2 | i1 | 0 | 0 | 1 | C1 | -1 | 4 | 2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | -2 | -2 | = | 0 | L1 | 1 | -2 | -2 | = |
| |||
| C1 | -2 | -1 | 4 | C1 | -2 | -1 | 2 | i2 | 0 | 0 | 1 | C1 | -1 | 4 | 2 |
| ||||||||||
| I2 | 0 | 0 | 0 | i2 | 0 | 0 | 1 | i1 | 0 | 0 | 1 | i2 | 0 | 0 | 1 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | -2 | -2 | = | 0 | C1 | -1 | 4 | 2 | = |
| |||
| C1 | -2 | -1 | 4 | C1 | -2 | -1 | 2 | L2 | 2 | -2 | -2 | L1 | 1 | -2 | -2 |
| ||||||||||
| L2 | 2 | 1 | -2 | L2 | 2 | 1 | -2 | i1 | 0 | 0 | 1 | L2 | 1 | -2 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -3 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | -2 | -2 | = | 2 | R2 | 1 | -3 | -2 | = |
| |||
| C1 | 2 | 1 | -2 | C1 | -2 | -1 | 2 | i1 | 0 | 0 | 1 | L1 | 1 | -2 | -2 |
| ||||||||||
| R2 | 2 | 1 | -3 | R2 | 2 | 1 | -2 | R2 | 2 | -3 | -2 | C | -1 | 4 | 2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | -2 | -2 | = | 0 | R1 | 1 | -3 | -2 | = |
| |||
| R1 | 2 | 1 | -3 | R1 | 2 | 1 | -2 | C1 | -2 | 4 | 2 | L1 | 1 | -2 | -2 |
| ||||||||||
| I2 | 0 | 0 | 0 | i2 | 0 | 0 | 1 | t | 0 | 1 | 0 | i2 | 0 | 0 | 1 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | L2 | 2 | -2 | -2 | = | -2 | L1 | 1 | -2 | -2 | = |
| |||
| R1 | 2 | 1 | -3 | L2 | 2 | 1 | -2 | R1 | 2 | -3 | -2 | L2 | 1 | -2 | -2 |
| ||||||||||
| L2 | 2 | 1 | -2 | R1 | 2 | 1 | -2 | i2 | 0 | 0 | 1 | R1 | 1 | -3 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | -2 | -2 | = | 2 | L1 | 1 | -2 | -2 | = |
| |||
| R1 | 2 | 1 | -3 | R1 | 2 | 1 | -2 | L2 | 2 | -2 | -2 | R2 | 1 | -3 | -2 |
| ||||||||||
| R2 | 2 | 1 | -3 | R2 | 2 | 1 | -2 | t | 0 | 1 | 0 | R1 | 1 | -3 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | -2 | -2 | = | 0 | L2 | 1 | -2 | -2 | = |
| |||
| L2 | 2 | 1 | -2 | i2 | 0 | 0 | 1 | L2 | 2 | -2 | -2 | i2 | 0 | 0 | 1 |
| ||||||||||
| I2 | 0 | 0 | 0 | L2 | 2 | 1 | -2 | t | 0 | 1 | 0 | L1 | 1 | -2 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | i2 | 0 | 0 | 1 | = | 0 | R2 | 2 | -3 | -2 | = | -2 | R2 | 1 | -3 | -2 | = |
| |||
| R2 | 2 | 1 | -3 | R2 | 2 | 1 | -2 | L2 | 2 | -2 | -2 | i2 | 0 | 0 | 1 |
| ||||||||||
| I2 | 0 | 0 | 0 | L1 | 2 | 1 | -2 | i2 | 0 | 0 | 1 | L1 | 1 | -2 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | i1 | 0 | 0 | 1 | = | 0 | L1 | 2 | -2 | -2 | = | 0 | L1 | 1 | -2 | -2 | = |
| |||
| L2 | 2 | 1 | -2 | t | 0 | 0 | 0 | C1 | -2 | 4 | 2 | L2 | 1 | -2 | -2 |
| ||||||||||
| R2 | 2 | 1 | -3 | C1 | -2 | -1 | 2 | R1 | 2 | -3 | -2 | R2 | 1 | -3 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | i1 | 0 | 0 | 1 | = | 0 | L1 | 2 | -2 | -2 | = | 4 | i1 | 0 | 0 | 1 | = |
| |||
| t | 0 | 0 | 1 | i2 | 0 | 0 | 1 | i2 | 0 | 0 | 1 | t | 0 | 1 | 0 |
| ||||||||||
| C1 | -2 | -1 | 4 | t | 0 | 0 | 0 | C1 | -2 | 4 | 2 | C1 | -1 | 4 | 2 |
| ||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | I1 | 0 | 0 | 1 | = | 0 | L1 | 2 | -2 | -2 | = | 0 | i1 | 0 | 0 | 1 | = |
| |||
| t | 0 | 0 | 1 | R1 | 2 | 1 | -2 | C1 | -2 | 4 | 2 | R1 | 1 | -3 | -2 |
| ||||||||||
| R1 | 2 | 1 | -3 | t | 0 | 0 | 0 | L2 | 2 | -2 | -2 | t | 0 | 1 | 0 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | I1 | 0 | 0 | 1 | = | 0 | C1 | -2 | 4 | 2 | = | 0 | i1 | 0 | 0 | 1 | = |
| |||
| t | 0 | 0 | 1 | t | 0 | 0 | 0 | R2 | 2 | -3 | -2 | t | 0 | 1 | 0 |
| ||||||||||
| I2 | 0 | 0 | 0 | L2 | 2 | 1 | -2 | L1 | 2 | -2 | -2 | i2 | 0 | 0 | 1 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | I1 | 0 | 0 | 1 | = | 0 | L1 | 2 | -2 | -2 | = | -2 | i1 | 0 | 0 | 1 | = |
| |||
| L2 | 2 | 1 | -2 | R2 | 2 | 1 | -2 | R1 | 2 | -3 | -2 | L2 | 1 | -2 | -2 |
| ||||||||||
| t | 0 | 0 | 1 | t | 0 | 0 | 0 | i2 | 0 | 0 | 1 | t | 0 | 1 | 0 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | C1 | -2 | -1 | 2 | = | 0 | L1 | 2 | -2 | -2 | = | 0 | i1 | 0 | 0 | 1 | = |
| |||
| R2 | 2 | 1 | -3 | R1 | 2 | 1 | -2 | R1 | 2 | -3 | -2 | t | 0 | 1 | 0 |
| ||||||||||
| t | 0 | 0 | 1 | i1 | 0 | 0 | 1 | L2 | 2 | -2 | -2 | R2 | 1 | -3 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | I1 | 0 | 0 | 1 | = | 0 | L1 | 2 | -2 | -2 | = | 0 | i1 | 0 | 0 | 1 | = |
| |||
| R1 | 2 | 1 | -3 | L2 | 2 | 1 | -2 | R2 | 2 | -3 | -2 | C1 | -1 | 4 | 2 |
| ||||||||||
| C1 | -2 | -1 | 4 | C1 | -2 | -1 | 2 | R1 | 2 | -3 | -2 | R1 | 1 | -3 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | I1 | 0 | 0 | 1 | = | 0 | L1 | 2 | -2 | -2 | = | 0 | i1 | 0 | 0 | 1 | = |
| |||
| C1 | -2 | -1 | 4 | C1 | -2 | -1 | 2 | i2 | 0 | 0 | 1 | C1 | -1 | 4 | 2 |
| ||||||||||
| I2 | 0 | 0 | 0 | R2 | 2 | 1 | -2 | L2 | 2 | -2 | -2 | i2 | 0 | 0 | 1 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | I1 | 0 | 0 | 1 | = | 0 | L1 | 2 | -2 | -2 | = | 2 | i1 | 0 | 0 | 1 | = |
| |||
| C1 | -2 | -1 | 4 | R1 | 2 | 1 | -2 | R2 | 2 | -3 | -2 | C1 | -1 | 4 | 2 |
| ||||||||||
| L2 | 2 | 1 | -2 | i2 | 0 | 0 | 1 | i2 | 0 | 0 | 1 | L2 | 1 | -2 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | I1 | 0 | 0 | 1 | = | 0 | L2 | 2 | -2 | -2 | = | 0 | i1 | 0 | 0 | 1 | = |
| |||
| C1 | -2 | -1 | 4 | R1 | 2 | 1 | -2 | R2 | 2 | -3 | -2 | C1 | -1 | 4 | 2 |
| ||||||||||
| R2 | 2 | 1 | -3 | L2 | 2 | 1 | -2 | L1 | 2 | -2 | -2 | R2 | 1 | -3 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | I1 | 0 | 0 | 1 | = | 0 | i1 | 0 | 0 | 1 | = | 2 | i1 | 0 | 0 | 1 | = |
| |||
| R1 | 2 | 1 | -3 | L2 | 2 | 1 | -2 | t | 0 | 1 | 0 | R1 | 1 | -3 | -2 |
| ||||||||||
| I2 | 0 | 0 | 0 | R1 | 2 | 1 | -2 | C1 | -2 | 4 | 2 | i2 | 0 | 0 | 1 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | I1 | 0 | 0 | 1 | = | 0 | i1 | 0 | 0 | 1 | = | -2 | i1 | 0 | 0 | 1 | = |
| |||
| R1 | 2 | 1 | -3 | R1 | 2 | 1 | -2 | R1 | 2 | -3 | -2 | R1 | 1 | -3 | -2 |
| ||||||||||
| L2 | 2 | 1 | -2 | R2 | 2 | 1 | -2 | t | 0 | 1 | 0 | L2 | 1 | -2 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | i1 | 0 | 0 | 1 | = | 0 | i1 | 0 | 0 | 1 | = | 0 | i1 | 0 | 0 | 1 | = |
| |||
| R1 | 2 | 1 | -3 | i2 | 0 | 0 | 1 | t | 0 | 1 | 0 | R2 | 1 | -3 | -2 |
| ||||||||||
| R2 | 2 | 1 | -3 | L2 | 2 | 1 | -2 | i2 | 0 | 0 | 1 | R1 | 1 | -3 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | i1 | 0 | 0 | 1 | = | 0 | i1 | 0 | 0 | 1 | = | -2 | i1 | 0 | 0 | 1 | = |
| |||
| L2 | 2 | 1 | -2 | R2 | 2 | 1 | -2 | L2 | 2 | -2 | -2 | i2 | 0 | 0 | 1 |
| ||||||||||
| I2 | 0 | 0 | 0 | i2 | 0 | 0 | 1 | t | 0 | 1 | 0 | L2 | 1 | -2 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | i1 | 0 | 0 | 1 | = | 0 | i1 | 0 | 0 | 1 | = | -2 | i1 | 0 | 0 | 1 | = |
| |||
| I2 | 0 | 0 | 0 | R2 | 2 | 1 | -2 | R2 | 2 | -3 | -2 | R2 | 1 | -3 | -2 |
| ||||||||||
| R2 | 2 | 1 | -3 | L2 | 2 | 1 | -2 | t | 0 | 1 | 0 | i2 | 0 | 0 | 1 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | C1 | -2 | -1 | 2 | = | 0 | i1 | 0 | 0 | 1 | = | -2 | i1 | 0 | 0 | 1 | = |
| |||
| R2 | 2 | 1 | -3 | R1 | 2 | 1 | -2 | R1 | 2 | -3 | -2 | R2 | 1 | -3 | -2 |
| ||||||||||
| L2 | 2 | 1 | -2 | t | 0 | 0 | 0 | C1 | -2 | 4 | 2 | L2 | 1 | -2 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| t | 0 | 0 | 1 | = | 0 | t | 0 | 0 | 0 | = | 0 | i1 | 0 | 0 | 1 | = | 0 | t | 0 | 1 | 0 | = |
| |||
| R1 | 2 | 1 | -3 | i2 | 0 | 0 | 1 | C1 | -2 | 4 | 2 | C1 | -1 | 4 | 2 |
| ||||||||||
| C1 | -2 | -1 | 4 | C1 | -2 | -1 | 2 | i2 | 0 | 0 | 1 | R1 | 1 | -3 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I2 | 0 | 0 | 0 | = | 0 | t | 0 | 0 | 0 | = | 0 | i1 | 0 | 0 | 1 | = | -4 | i2 | 0 | 0 | 1 | = |
| |||
| C1 | -2 | -1 | 4 | C1 | -2 | -1 | 2 | C1 | -2 | 4 | 2 | C1 | -1 | 4 | 2 |
| ||||||||||
| t | 0 | 0 | 1 | L2 | 2 | 1 | -2 | L2 | 2 | -2 | -2 | t | 0 | 1 | 0 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| t | 0 | 0 | 1 | = | 0 | C1 | -2 | -1 | 2 | = | 0 | i1 | 0 | 0 | 1 | = | -2 | t | 0 | 1 | 0 | = |
| |||
| C1 | -2 | -1 | 4 | R2 | 2 | 1 | -2 | R2 | 2 | -3 | -2 | C1 | -1 | 4 | 2 |
| ||||||||||
| L2 | 2 | 1 | -2 | t | 0 | 0 | 0 | C1 | -2 | 4 | 2 | L2 | 1 | -2 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| t | 0 | 0 | 1 | = | 0 | i2 | 0 | 0 | 1 | = | 0 | i1 | 0 | 0 | 1 | = | 0 | C1 | -1 | 4 | 2 | = |
| |||
| C1 | -2 | -1 | 4 | L1 | 2 | 1 | -2 | i2 | 0 | 0 | 1 | R2 | 1 | -3 | -2 |
| ||||||||||
| R2 | 2 | 1 | -3 | t | 0 | 0 | 0 | R1 | 2 | -3 | -2 | t | 0 | 1 | 0 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I2 | 0 | 0 | 0 | = | 0 | i2 | 0 | 0 | 1 | = | 0 | i1 | 0 | 0 | 1 | = | 2 | i2 | 0 | 0 | 1 | = |
| |||
| R1 | 2 | 1 | -3 | R1 | 2 | 1 | -2 | R1 | 2 | -3 | -2 | R1 | 1 | -3 | -2 |
| ||||||||||
| t | 0 | 0 | 1 | t | 0 | 0 | 0 | L2 | 2 | -2 | -2 | t | 0 | 1 | 0 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| t | 0 | 0 | 1 | = | 0 | t | 0 | 0 | 0 | = | 0 | i1 | 0 | 0 | 1 | = | 0 | R1 | 1 | -3 | -2 | = |
| |||
| R1 | 2 | 1 | -3 | R1 | 2 | 1 | -2 | R1 | 2 | -3 | -2 | t | 0 | 1 | 0 |
| ||||||||||
| L2 | 2 | 1 | -2 | L2 | 2 | 1 | -2 | R2 | 2 | -3 | -2 | L2 | 1 | -2 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| t | 0 | 0 | 1 | = | 0 | R2 | 2 | 1 | -2 | = | 0 | t | 0 | 0 | 1 | = | 2 | R2 | 1 | -3 | -2 | = |
| |||
| R1 | 2 | 1 | -3 | R1 | 2 | 1 | -2 | i2 | 0 | 0 | 1 | t | 0 | 1 | 0 |
| ||||||||||
| R2 | 2 | 1 | -3 | t | 0 | 0 | 0 | R2 | 2 | -3 | -2 | R1 | 1 | -3 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I2 | 0 | 0 | 0 | = | 0 | t | 0 | 0 | 0 | = | 0 | i1 | 0 | 0 | 1 | = | 0 | i2 | 0 | 0 | 1 | = |
| |||
| L2 | 2 | 1 | -2 | i2 | 0 | 0 | 1 | R2 | 2 | -3 | -2 | L2 | 1 | -2 | -2 |
| ||||||||||
| t | 0 | 0 | 1 | L2 | 2 | 1 | -2 | i2 | 0 | 0 | 1 | t | 0 | 1 | 0 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| R2 | 2 | 1 | -3 | = | 0 | R2 | 2 | 1 | -2 | = | 0 | i1 | 0 | 0 | 1 | = | -2 | R2 | 1 | -3 | -2 | = |
| |||
| I2 | 0 | 0 | 0 | i2 | 0 | 0 | 1 | L2 | 2 | -2 | -2 | i2 | 0 | 0 | 1 |
| ||||||||||
| t | 0 | 0 | 1 | t | 0 | 0 | 0 | R2 | 2 | -3 | -2 | t | 0 | 1 | 0 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| R2 | 2 | 1 | -3 | = | 0 | R2 | 2 | 1 | -2 | = | 0 | R1 | 2 | -3 | -2 | = | -2 | R2 | 1 | -3 | -2 | = |
| |||
| t | 0 | 0 | 1 | L2 | 2 | 1 | -2 | i2 | 0 | 0 | 1 | L2 | 1 | -2 | -2 |
| ||||||||||
| L2 | 2 | 1 | -2 | t | 0 | 0 | 0 | C1 | -2 | 4 | 2 | t | 0 | 1 | 0 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| R1 | 2 | 1 | -3 | = | 0 | C1 | -2 | -1 | 2 | = | 0 | t | 0 | 1 | 0 | = | 2 | R1 | 1 | -3 | -2 | = |
| |||
| C1 | -2 | -1 | 4 | R1 | 2 | 1 | -2 | C1 | 2 | -2 | -1 | C1 | -1 | 4 | 2 |
| ||||||||||
| I2 | 0 | 0 | 0 | i2 | 0 | 0 | 1 | i2 | 0 | 0 | 1 | i2 | 0 | 0 | 1 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| R1 | 2 | 1 | -3 | = | 0 | R1 | 2 | 1 | -2 | = | 0 | L2 | 2 | -2 | -2 | = | 4 | C1 | -1 | 4 | 2 | = |
| |||
| L2 | 2 | 1 | -2 | L2 | 2 | 1 | -2 | C1 | -2 | 4 | 2 | R1 | 1 | -3 | -2 |
| ||||||||||
| C1 | -2 | -1 | 4 | C1 | -2 | -1 | 2 | i2 | 0 | 0 | 1 | L2 | 1 | -2 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| R2 | 2 | 1 | -3 | = | 0 | R1 | 2 | 1 | -2 | = | 0 | R2 | 2 | -3 | -2 | = | 2 | C1 | -1 | 4 | 2 | = |
| |||
| R1 | 2 | 1 | -3 | R2 | 2 | 1 | -2 | C1 | -2 | 4 | 2 | R1 | 1 | -3 | -2 |
| ||||||||||
| C1 | -2 | -1 | 4 | C1 | -2 | -1 | 2 | i2 | 0 | 0 | 1 | R2 | 1 | -3 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| C1 | -2 | -1 | 4 | = | 0 | C1 | -2 | -1 | 2 | = | 0 | R1 | 2 | -3 | -2 | = | -2 | i2 | 0 | 0 | 1 | = |
| |||
| L2 | 2 | 1 | -2 | L2 | 2 | 1 | -2 | i2 | 0 | 0 | 1 | L2 | 1 | -2 | -2 |
| ||||||||||
| I2 | 0 | 0 | 0 | i2 | 0 | 0 | 1 | t | 0 | 1 | 0 | C1 | -1 | 4 | 2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| C1 | -2 | -1 | 4 | = | 0 | C1 | -2 | -1 | 2 | = | 0 | i2 | 0 | 0 | 1 | = | 2 | C1 | -1 | 4 | 2 | = |
| |||
| L2 | 2 | 1 | -2 | R2 | 2 | 1 | -2 | L2 | 2 | -2 | -2 | R2 | 1 | -3 | -2 |
| ||||||||||
| R2 | 2 | 1 | -3 | i2 | 0 | 0 | 1 | t | 0 | 1 | 0 | i2 | 0 | 0 | 1 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | -2 | -2 | = | 0 | L2 | 1 | -2 | -2 | = |
| |||
| L2 | 2 | 1 | -2 | i2 | 0 | 0 | 1 | L2 | 2 | -2 | -2 | i2 | 0 | 0 | 1 |
| ||||||||||
| I2 | 0 | 0 | 0 | L2 | 2 | 1 | -2 | t | 0 | 1 | 0 | L1 | 1 | -2 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I | |||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | C | -2 | 4 | 2 | = | 0 | L1 | 1 | -2 | -2 | = | 0 | |||
| i1 | 0 | 0 | 0 | i1 | 0 | 0 | 1 | R1 | 2 | -3 | -2 | i1 | 0 | 0 | 1 | |||||||||||
| i2 | 0 | 0 | 0 | i2 | 0 | 0 | 1 | L2 | 2 | -2 | -2 | i2 | 0 | 0 | 1 | |||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I | |||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | L1 | 2 | 1 | -2 | = | 0 | R1 | 2 | -3 | -2 | = | 0 | L2 | 1 | -2 | -2 | = | -1 | |||
| t | 0 | 0 | 1 | t | 0 | 0 | 0 | t | 0 | 1 | 0 | R2 | 1 | -3 | -2 | |||||||||||
| R1 | 2 | 1 | -3 | R1 | 2 | 1 | -2 | L2 | 2 | -2 | -2 | i2 | 0 | 0 | 1 | |||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| I1 | 0 | 0 | 0 | = | 0 | i1 | 0 | 0 | 1 | = | 0 | i1 | 0 | 0 | 1 | = | 0 | i1 | 0 | 0 | 1 | = |
| |||
| R1 | 2 | 1 | -3 | i2 | 0 | 0 | 1 | t | 0 | 1 | 0 | R2 | 1 | -3 | -2 |
| ||||||||||
| R2 | 2 | 1 | -3 | L2 | 2 | 1 | -2 | i2 | 0 | 0 | 1 | R1 | 1 | -3 | -2 |
| ||||||||||
| ||||||||||||||||||||||||||
| L | M | T | L | M | I | L | T | I | M | T | I |
| ||||||||||||||
| L1 | 2 | 1 | -2 | = | 0 | i1 | 0 | 0 | 1 | = | 0 | L1 | 2 | -2 | -2 | = | 0 | L1 | 1 | -2 | -2 | = |
| |||
| L2 | 2 | 1 | -2 | t | 0 | 0 | 0 | C1 | -2 | 4 | 2 | i2 | 0 | 0 | 1 |
| ||||||||||
| R2 | 2 | 1 | -3 | C1 | -2 | -1 | 2 | R1 | 2 | -3 | -2 | R1 | 1 | -3 | -2 |
| ||||||||||
|
Похожие работы
... в ОАО «Авиалинии Дагестана» персональную ответственность работников аппарата управления за исполнение воли вышестоящих органов. Организационно-распорядительные методы управления на предприятии разнообразны. Рычагами воздействия являются регламенты, нормы, инструкции, директивные требования, ответственность и полномочия, приказы, распоряжения, указания. Выделяют три группы организационно- ...
... могут быть реализованы в виде сортирующих сетей Батчера, расширенных сетей или параллельных Баньяновидных плоскостей [12,14]. 2. КОММУТАЦИЯ В СЕТЯХ АТМ 2.1 ПРИНЦИПЫ ПРОЕКТИРОВАНИЯ КОММУТАТОРОВ Технология асинхронного режима передачи (Asynchronous Transfer Mode, ATM) наилучшим образом подходит для построения широкополосных цифровых сетей с интеграцией служб (Broadband Integrated ...
... климата, изучить групповые нормы и ценности, структуру ролей или систему властных отношений, с целью выявить истоки возможных конфликтов и их разрешения. Глава 2. Практическое применение социологических методов исследования на примере компании 2.1 «Русская Аудиторская Компания» Головная компания холдинга - "Русская Аудиторская Компания" - была создана в 1997 году. Компания способна решать ...
... один почти неизвестный в России, но достаточно мощный и популярный в мире продукт - Visula компании Zuken. Продукты этой компании обеспечивают сквозной цикл проектирования и предлагают мощные средства моделирования и синтеза программируемой логики с последующей разработкой печатной платы. Здесь имеется стандартный набор инструментария, а также собственные средства авторазмещения и автотрассировки ...
0 комментариев