Навигация
Похибки наближення ермітовими сплайнами
4. Похибки наближення ермітовими сплайнами
Максимальна похибка ![]() рівномірного наближення нелінійними ермітовими сплайнами з парною кількістю параметрів у ланці має вигляд
рівномірного наближення нелінійними ермітовими сплайнами з парною кількістю параметрів у ланці має вигляд
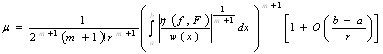 , (37)
, (37)
а для ермітових сплайнів з непарною кількістю параметрів
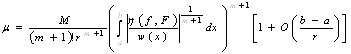 (38)
(38)
де ![]() - кількість ланок сплайна на інтервалі
- кількість ланок сплайна на інтервалі ![]() ,
, ![]() - вагова функція,
- вагова функція, ![]() - ядро похибки наближення,
- ядро похибки наближення, ![]() - дефект ермітового сплайна,
- дефект ермітового сплайна, ![]() . Для ермітового сплайна з ланкою (13) кількість параметрів
. Для ермітового сплайна з ланкою (13) кількість параметрів ![]() , дефект сплайна за означенням
, дефект сплайна за означенням ![]() , величина
, величина ![]() . Щоб скористатись формулами (37) і(38), потрібно мати вираз для ядра похибки наближення
. Щоб скористатись формулами (37) і(38), потрібно мати вираз для ядра похибки наближення ![]() , який би не залежав від параметрів
, який би не залежав від параметрів ![]() ланки сплайна
ланки сплайна ![]()
![]() . Вирази для конкретних ядер можна знайти, використовуючи властивості ядер похибок, які випливають із обмінних теорем.
. Вирази для конкретних ядер можна знайти, використовуючи властивості ядер похибок, які випливають із обмінних теорем.
Теорема 1. Нехай для функції ![]()
![]() при
при ![]() існує єдине наближення ермітовим сплайном з парною кількістю параметрів з вузлами
існує єдине наближення ермітовим сплайном з парною кількістю параметрів з вузлами ![]() і ланками вигляду
і ланками вигляду
![]() (39)
(39)
![]()
Тоді для функції ![]() на проміжку
на проміжку ![]() з тими ж вузлами існує єдине наближення ермітовим сплайном з парною кількістю параметрів і ланками вигляду
з тими ж вузлами існує єдине наближення ермітовим сплайном з парною кількістю параметрів і ланками вигляду
![]() (40)
(40)
Нехай ![]() — найбільша відносна похибка наближення функції
— найбільша відносна похибка наближення функції ![]() на проміжку
на проміжку![]()
![]() ермітовим сплайном з ланкою (39), а
ермітовим сплайном з ланкою (39), а ![]() — найбільша відносна похибка наближення функції
— найбільша відносна похибка наближення функції ![]() на проміжку
на проміжку ![]() ермітовим сплайном з ланкою вигляду (40). В цьому випадку між параметрами наближень мають місце співвідношення;
ермітовим сплайном з ланкою вигляду (40). В цьому випадку між параметрами наближень мають місце співвідношення;
![]() (41)
(41)
![]() . (42)
. (42)
Доведення. Сплайн з ланкою вигляду (39) характеризується системою рівнянь
![]() (43)
(43)
![]()
а сплайн з ланкою вигляду (40) — системою рівнянь
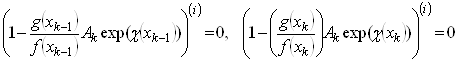 (44)
(44)
![]()
Надалі опускаємо індекс, який вказує на приналежність параметра до ![]() -ї ланки. Із системи (44) при
-ї ланки. Із системи (44) при ![]() матимемо
матимемо
![]() .
.
Подамо ![]() як
як ![]() , про логарифмуємо це рівняння і отримаємо
, про логарифмуємо це рівняння і отримаємо
![]() ,
,
де ![]() . Тобто при
. Тобто при ![]() рівняння із системи (44) зведене до рівняння із системи (43).
рівняння із системи (44) зведене до рівняння із системи (43).
При ![]() рівняння із системи (44) має вигляд
рівняння із системи (44) має вигляд
![]() .
.
Помножимо чисельник і знаменник цього рівняння на ![]()
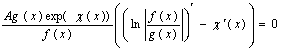 .
.
Оскільки з умов теореми ![]() не дорівнюють нулю, то рівність досягається за умови, що
не дорівнюють нулю, то рівність досягається за умови, що
![]() ,
,
а це і є рівняння із системи (43) при ![]() .
.
Використовуючи метод математичної індукції, покажемо, що рівняння із системи (44) зводиться до рівнянь із системи (43) за довільних ![]() . Нехай це доведено для
. Нехай це доведено для ![]() . Доведемо для
. Доведемо для ![]() . Рівняння із системи (43) при
. Рівняння із системи (43) при ![]() :
:
![]() .
.
Для ![]() рівняння із системи (44) має вигляд
рівняння із системи (44) має вигляд
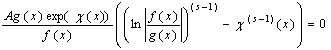 .
.
Про диференціюємо це рівняння і отримаємо
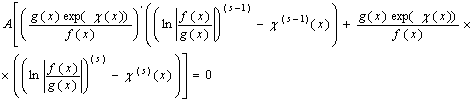
Перший доданок в квадратних дужках дорівнює нулю через рівність нулю останнього співмножника. Рівняння набере вигляду
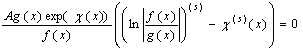 .
.
Множник, який стоїть перед квадратними дужками, не дорівнює нулю з умов теореми, отже нулю дорівнює вираз у квадратних дужках. А це і є рівняння із системи (43). Отже, ми довели, що за довільних ![]() рівняння в системах (43) і (44) еквівалентні, а , значить, і системи рівносильні. Тому
рівняння в системах (43) і (44) еквівалентні, а , значить, і системи рівносильні. Тому ![]() при
при ![]() , а
, а ![]() .
.
Доведемо справедливість відношення (43) для похибок наближення. Оскільки системи (43) і (44) рівносильні, то точки, в яких досягається максимальні похибки, збігаються. Нехай ![]() точка , в якій досягається максимальна похибка наближення функції
точка , в якій досягається максимальна похибка наближення функції ![]() ермітовим сплайном з ланкою (39). Тоді похибка в цій точці дорівнює
ермітовим сплайном з ланкою (39). Тоді похибка в цій точці дорівнює
![]() .
.
Із цієї рівності випливає, що
![]() .
.
У правій частині маємо відносну похибку наближення функції ![]() ермітовим сплайном з ланкою (40) на проміжку
ермітовим сплайном з ланкою (40) на проміжку ![]() . Звідси
. Звідси ![]() . Теорема доведена.
. Теорема доведена.
За допомогою цієї теореми можна отримувати наближення ермітовим сплайном з ланкою (40) шляхом знаходження наближення ермітовим сплайном з простішою ланкою (39). Зокрема, наближення до функції ![]() ермітовим сплайном з ланкою вигляду
ермітовим сплайном з ланкою вигляду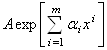 зводиться до наближення функції
зводиться до наближення функції ![]() ермітовим сплайном з ланкою
ермітовим сплайном з ланкою ![]() . При цьому найбільша відносна похибка першого наближення виражається через найбільшу абсолютну похибку другого наближення.
. При цьому найбільша відносна похибка першого наближення виражається через найбільшу абсолютну похибку другого наближення.
Теорема 2. Нехай для функції ![]()
![]()
![]() при
при ![]() існує єдине наближення ермітовим сплайном з непарною кількістю параметрів з вузлами
існує єдине наближення ермітовим сплайном з непарною кількістю параметрів з вузлами ![]() і ланками вигляду
і ланками вигляду
![]()
![]() (45)
(45)
Тоді для функції ![]() на проміжку
на проміжку ![]() з тими ж вузлами існує єдине наближення ермітовим сплайном з непарною кількістю параметрів і ланками вигляду
з тими ж вузлами існує єдине наближення ермітовим сплайном з непарною кількістю параметрів і ланками вигляду
![]() (46)
(46)
Нехай ![]() — найбільша відносна похибка наближення функції
— найбільша відносна похибка наближення функції ![]() на проміжку
на проміжку ![]() ермітовим сплайном з ланкою (45), а
ермітовим сплайном з ланкою (45), а ![]() — найбільша відносна похибка наближення функції
— найбільша відносна похибка наближення функції ![]() на проміжку
на проміжку ![]() ермітовим сплайном з ланкою вигляду (45). В цьому випадку між параметрами наближень мають місце співвідношення;
ермітовим сплайном з ланкою вигляду (45). В цьому випадку між параметрами наближень мають місце співвідношення;
![]() (47)
(47)
![]() . (48)
. (48)
Доведення. В теоремі 1 до системи рівнянь (42) додається рівняння
![]() , (49)
, (49)
а до системи (43) рівняння
![]() (50)
(50)
Для доведення цієї теореми для ермітових сплайнів з непарною кількістю параметрів необхідно довести еквівалентність рівнянь (48) і (50). Для цього перепишемо (50) у вигляді
![]() .
.
Про логарифмуємо і отримаємо
![]() ,
,
де із умови теореми 2 ![]() , а
, а ![]() .Тобто рівняння (50) зведено до (49). Теорему доведено.
.Тобто рівняння (50) зведено до (49). Теорему доведено.
Властивість 1. Нехай ![]() при
при ![]() . Тоді
. Тоді
![]() (51)
(51)
Доведення. Із теорем 1 і 2 випливає, що наближення функції ![]() на
на ![]() ермітовим сплайном з ланкою
ермітовим сплайном з ланкою ![]() може бути знайдено через наближення функції
може бути знайдено через наближення функції ![]() на цьому проміжку ермітовим сплайном з ланкою
на цьому проміжку ермітовим сплайном з ланкою ![]() . При цьому із формули (42) випливає, що максимальна відносна похибка
. При цьому із формули (42) випливає, що максимальна відносна похибка ![]() першого наближення виражається через максимальну абсолютну похибку
першого наближення виражається через максимальну абсолютну похибку ![]() другого наближення
другого наближення
![]()
Із рівності похибок і формули (37) матимемо
![]() .
.
Цей вираз справедливий для довільних ![]() ,
, ![]() і проміжків
і проміжків ![]() лише в тому випадку, якщо підінтегральні вирази рівні між собою. Із їх рівності випливає вираз (51).
лише в тому випадку, якщо підінтегральні вирази рівні між собою. Із їх рівності випливає вираз (51).
Тепер можна вивести аналітичний вираз для ядра похибки наближення ![]() ермітовим сплайном з ланкою (1). Ядро похибки наближення многочленом
ермітовим сплайном з ланкою (1). Ядро похибки наближення многочленом ![]() степеня
степеня ![]() має вигляд
має вигляд ![]() . Застосувавши формулу (52), отримаємо
. Застосувавши формулу (52), отримаємо
![]() . (52)
. (52)
Для ермітового сплайна з експоненціальною ланкою (6) ядро матиме такий вигляд:
![]() .
.
А для ланки (13)
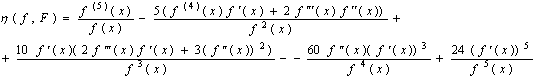
0 комментариев