Навигация
Рівномірне наближення ермітовими сплайнами
5. Рівномірне наближення ермітовими сплайнами
Наближення функції ![]() ермітовим сплайном
ермітовим сплайном ![]() називаємо рівномірним наближенням з заданою похибкою
називаємо рівномірним наближенням з заданою похибкою ![]() , якщо
, якщо ![]()
![]() , де
, де ![]() - вага наближення,
- вага наближення,![]() .
.
Алгоритм рівномірного наближення ермітовими сплайнами з заданою похибкою. Алгоритм не залежить від виду сплайна.
1. Будуємо ланку нелінійного ермітового сплайна на всьому інтервалі ![]() . Ліва границя
. Ліва границя ![]() права
права ![]()
2. Знаходимо похибку наближення ![]() .
.
3. Якщо![]() , то наближення побудоване. Кінець.
, то наближення побудоване. Кінець.
4. Якщо ![]() , то зсуваємо праву границю інтервалу вліво, поки похибка на даному інтервалі не стане меншою від заданої похибки
, то зсуваємо праву границю інтервалу вліво, поки похибка на даному інтервалі не стане меншою від заданої похибки ![]() . Допустимо, що при
. Допустимо, що при ![]() -му зсуві границі вліво (т.
-му зсуві границі вліво (т. ![]() )похибка рівна
)похибка рівна ![]() , а на попередньому кроці
, а на попередньому кроці ![]() ( права границя
( права границя ![]() ). Тоді можна знайти таку праву границю
). Тоді можна знайти таку праву границю ![]() , при якій похибка
, при якій похибка ![]() буде як завгодно мало відрізнятися від заданої
буде як завгодно мало відрізнятися від заданої ![]() . Точку
. Точку ![]() можна знайти одним із відомих способів, наприклад методом ділення відрізка навпіл або методом хорд.
можна знайти одним із відомих способів, наприклад методом ділення відрізка навпіл або методом хорд.
5. Запам’ятовуємо границі ланки і параметри ермітового сплайна.
6. Лівою границею наступної ланки є права границя попередньої ланки. Правою границею можна завжди вважати т. ![]() , але можна також екстраполювати точкою
, але можна також екстраполювати точкою ![]() де
де ![]() - довжина попередньої ланки.
- довжина попередньої ланки.
7. Будуємо сплайн і знаходимо похибку.
8. Якщо ![]() , то переходимо до пункту 4.
, то переходимо до пункту 4.
9. Якщо![]() і
і ![]() , то
, то ![]() і переходимо до пункту 7. В протилежному випадку, при
і переходимо до пункту 7. В протилежному випадку, при ![]() , запам’ятовуємо границі та параметри нелінійного ермітового сплайна. Рівномірне наближення з заданою похибкою знайдено.
, запам’ятовуємо границі та параметри нелінійного ермітового сплайна. Рівномірне наближення з заданою похибкою знайдено.
Очевидно, що описаний алгоритм приводить до єдиного рішення, якщо наближувана функція ![]() і сплайн
і сплайн ![]() такі що функція похибки
такі що функція похибки
![]() ,
,
є неспадною функцією від ![]() . Для цього достатньо, щоб ядро наближення
. Для цього достатньо, щоб ядро наближення ![]() при
при ![]() .
.
Із означення ермітового сплайна можна запропонувати інший алгоритм знаходження його параметрів. При ![]() (парна кількість параметрів) параметри визначаються із тих же рівнянь, що й у випадку фіксованих вузлів, до яких додаються рівняння для точки екстремуму
(парна кількість параметрів) параметри визначаються із тих же рівнянь, що й у випадку фіксованих вузлів, до яких додаються рівняння для точки екстремуму![]() і правої границі
і правої границі ![]() .
.
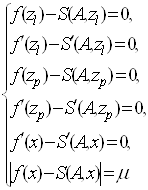 (53)
(53)
![]()
Потрібно знайти залежність ![]() від
від ![]() . Для деяких вузлів ланок ермітових сплайнів, а саме ланок у вигляді многочлена, відношення многочлена до лінійної функції, добутку степеневої і експоненціальної функцій, степеневого виразу від многочлена параметри
. Для деяких вузлів ланок ермітових сплайнів, а саме ланок у вигляді многочлена, відношення многочлена до лінійної функції, добутку степеневої і експоненціальної функцій, степеневого виразу від многочлена параметри ![]() сплайна знаходяться в аналітичному вигляді із перших чотирьох рівнянь системи (53).
сплайна знаходяться в аналітичному вигляді із перших чотирьох рівнянь системи (53).
Вони залежать від ![]() і значень функції та її похідної в цих точках. Коефіцієнти можна підставити в п’яте і шосте рівняння системи. В результаті система шести рівнянь з шістьома невідомими зводиться до системи двох рівнянь з двома невідомими
і значень функції та її похідної в цих точках. Коефіцієнти можна підставити в п’яте і шосте рівняння системи. В результаті система шести рівнянь з шістьома невідомими зводиться до системи двох рівнянь з двома невідомими ![]() :
:
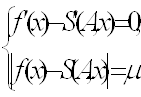 (54)
(54)
Система (54) є системою трансцендентних рівнянь. Її можна розв’язати, використовуючи відомі наближені методи знаходження коренів трансцендентних систем.
Висновки
В багатьох технічних задачах використовується кускова апроксимація однозначних функцій. Застосування у такій задачі нелінійних виразів з метою наближення викликає труднощі через відсутність ефективних алгоритмів для визначення їх параметрів. Для цієї задачі є зручними кускові наближення (сплайн-наближення). У роботі наведений приклад побудови ермітового сплайна з експоненціальною і многочленною ланками. Оскільки похибка ермітового сплайна з експоненціальною ланкою в деяких випадках є меншою, ніж у многочленного ермітового сплайна, то їх доцільно застосовувати для наближення функцій. Також побудовано алгоритми рівномірного наближення ермітовими сплайнами.
Викладацька практика
1.10.2009 – 3 пара.
Лекція з курсу "Теорія масового обслуговування".
Тема: "Потоки Пальма".
Заняття проводилось для груп СІМ51 магістри і спеціалісти.
2.10.2009 – 1 пара.
Лабораторна робота з курсу "Чисельні методи".
Тема: "Однокрокові методи чисельного розвязування задачі Коші для звичайних диференціальних рівнянь"
Заняття проводилось для групи ПМ41.
2.10.2009. – 3 пара.
Практичне заняття з курсу "Теорія масового обслуговування".
Тема: "Найпростіший потік"
Заняття проводилось для груп СІМ51 магістри і спеціалісти.
Опис програми
Програма Hermit’s spline шукає балансне наближення функцій ермітовими сплайнами. Головне вікно програми розділене на дві частини: ліву і праву. У лівій частині є три закладки: перша призначена для виводу результатів програми, друга для виводу графіків функції і сплайну; третя для виводу графіку похибки наближення. У правій частині є поля для вводу меж інтервалу і похибки. Також є перемикачі для вибору виду сплайна і функції.
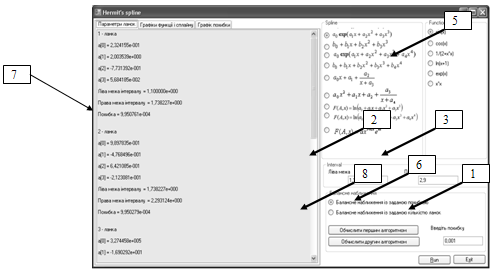
Для роботи програми треба виконати наступні дії:
· у поля "2" "3" потрібно ввести межі інтервалу на якому функція визначена і диференційовна;
· у поле "1" треба ввести похибку;
· вибрати вид сплайна 4;
· вибрати функцію 5;
· далі натиснути кнопку "6", яка викликає функцію, що будує балансне наближення із заданою похибкою;
· для побудови балансного наближення із заданою кількістю ланок треба натиснути кнопку "8";
· вивід результатів буде у полі "7";
· щоб переглянути графіки функції і сплайну потрібно натиснути на закладку 9;
· щоб переглянути графік похибки наближення потрібно натиснути на закладку 10;
Опис основних функцій програми:
· void ermit_1(double *a, double x0, double x1); - функція пошуку коефіцієнтів ермітового сплайна з ланками виду ![]() ;
;
· void ermit_2(double *a, double x0, double x1); - функція пошуку коефіцієнтів ермітового сплайна з ланками виду ![]() ;
;
· void ermit_3(double *a, double x0, double x2); - функція пошуку коефіцієнтів ермітового сплайна з ланками виду ![]() ;
;
· void ermit_4(double *b, double x0, double x2); - функція пошуку коефіцієнтів ермітового сплайна з ланками виду ![]() ;
;
· void ermit_5(double *a, double zl, double zp); - функція пошуку коефіцієнтів ермітового сплайна з ланками виду![]() ;
;
· void ermit_rp(double *a, double a1, double b1, double nyu, int n); - рівномірне наближення ермітовими сплайнами із заданною похибкою;
· void ermit_rl (double*a, double zl, double b1, int n, int p, int r); - рівномірне наближення ермітовими сплайнами із заданною кількістю ланок.
Література
1. Пізюр Я.В., Попов Б.О. Рівномірне наближення ермітовими сплайнами з парною кількістю параметрів.// Контрольно-вимірювальна техніка.- 1993. – Вип. 50. – С. 8-13
2. Пізюр Я.В. Наближення функцій ермітовими сплайнами з експоненціальними ланками// Вісник НУ "Львівська політехніка". "Фізико-математичні науки" №566, 2006, – С. 68-75.
3. Зав’ялов Ю.С., Квасов Б.И., Мірошниченко В.Л. Методи сплайн функцій. – М.: Наука, 1980. – 352 с.
Додаток
Код програми.
private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {
double zl, zp, x;
zl=Double::Parse(textBox3->Text);
zp=Double::Parse(textBox4->Text);
x =(zl+zp)/2;
int p=2,n=5;
if((s1->Checked==true)||(s2->Checked==true)||(s5->Checked==true)||(s7->Checked==true)||(s9->Checked==true)){
n=4;p=1;
}
double *a = new double[n];
if (s1->Checked == true) {
ermit_1(a, zl, zp, p);
}
if (s2->Checked == true) {
ermit_2(a, zl, zp, p);
}
if (s3->Checked == true) {
ermit_3(a, zl, zp, p);
}
if (s4->Checked == true) {
ermit_4(a, zl, zp, p);
}
if (s5->Checked == true) {
ermit_5(a, zl, zp, p);
}
if (s6->Checked == true) {
ermit_6(a, zl, zp, p);
}
if (s7->Checked == true) {
ermit_8(a, zl, zp, p);
}
if (s8->Checked == true) {
ermit_9(a, zl, zp, p);
}
if (s9->Checked == true) {
ermit_7(a, zl, zp, p);
}
chart1->Series["Function"]->Points->Clear();
chart1->Series["Spline"]->Points->Clear();
chart2->Series["error"]->Points->Clear();
double t,ch1,ch2,ch3;
for(t = zl; t <= zp; t += 0.01)
{
ch1 = f(t,1);
ch2 = sp(a,t);
ch3 = epx_p(a,t,1);
chart1->Series["Function"]->Points->AddXY(t, ch1);
chart1->Series["Spline"]->Points->AddXY(t, ch2);
chart2->Series["error"]->Points->AddXY(t, ch3);
}
}
//~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
double epx_p(double *a, double x, int p) {
return Math::Abs((f(x, p) - sp(a, x)) / w(x));
}
//~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
public: double f(double x, int p) {
if(f1->Checked==true){
return Math::Sin(x);
}
if(f2->Checked==true){
return Math::Cos(x);
}
if(f3->Checked==true){
return 1 / (2 + x * x);
}
if(f4->Checked==true){
return Math::Log(x + 1);
}
if(f5->Checked==true){
return Math::Exp(x);
}
if(f6->Checked==true){
return x*x;
}
return -1;
}
//~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
public: double fp(double x, int p) {
if(f1->Checked==true){
return Math::Cos(x);
}
if(f2->Checked==true){
return -Math::Sin(x);
}
if(f3->Checked==true){
return (-2* x ) / ((2 + x * x) * (2 + x * x));
}
if(f4->Checked==true){
return 1 / (x + 1);
}
if(f5->Checked==true){
return Math::Exp(x);
}
if(f6->Checked==true){
return 2*x;
}
return -1;
}
//*****************************************
public: void ermit_1(double *a, double x0, double x1, int p) {
a[3] = (fp(x1, p) / f(x1, p) + fp(x0, p) / f(x0, p) + 2 * (Math::Log(f(x0, p)
/ f(x1, p)) / (x1 - x0))) / ((x1 - x0) * (x1 - x0));
a[2] = ((2* x0 * x0 - x0 * x1 - x1 * x1) * a[3] - (fp(x0, p) / f(x0, p))
- (Math::Log(f(x0, p) / f(x1, p)) / (x1 - x0))) / (x1 - x0);
a[1] = (1 / (x1 - x0)) * (Math::Log(f(x1, p) / f(x0, p)) - a[3] * (x1 * x1 * x1
- x0 * x0 * x0) - a[2] * (x1 * x1 - x0 * x0));
a[0] = f(x0, p) * Math::Exp(-(a[1] * x0 + a[2] * x0 * x0 + a[3] * x0 * x0 * x0));
}
/////////////////////////////////////////////////////////////////////////////
void ermit_2(double *b, double x0, double x1, int p) {
double h;
h = x1 - x0;
b[3] = 2 * ((fp(x1, p) + fp(x0, p)) / 2 - (f(x1, p) - f(x0, p)) / h) / (h
* h);
b[2] = 0.5 * ((fp(x1, p) - fp(x0, p)) / h - 3* b [3] * (x0 + x1));
b[1] = fp(x1, p) - 2* b [2] * x1 - 3* b [3] * x1 * x1;
b[0] = 0.5 * (f(x1, p) + f(x0, p) - b[3] * (x0 * x0 * x0 + x1 * x1 * x1)
- b[2] * (x0 * x0 + x1 * x1) - b[1] * (x0 + x1));
}
////////////////////////////////////////////////////////////////
void ermit_3(double *a, double x0, double x2, int p) {
double a1, a2, a3, b1, b2, b3, z1, z2, z3, g1, g2, g3;
double x1;
x1 = (x0 + x2) / 2;
a1 = Math::Log(f(x1, p) / f(x0, p)) / (x1 - x0) - Math::Log(f(x2, p) / f(x0, p)) / (x2 - x0);
b1 = (x1 + x0) * (x1 * x1 + x0 * x0) - (x2 + x0) * (x2 * x2 + x0 * x0);
z1 = x1 * x1 + x1 * x0 - x2 * x2 - x2 * x0;
g1 = x1 - x2;
a2 = Math::Log(f(x1, p) / f(x0, p)) / (x1 - x0) - fp(x0, p) / f(x0, p);
b2 = x1 * x1 * x1 + x0 * x1 * (x0 + x1) - 3* x0 * x0 * x0;
z2 = x1 * x1 + x0 * x1 - 2* x0 * x0;
g2 = x1 - x0;
a3 = Math::Log(f(x1, p) / f(x0, p)) / (x1 - x0) - fp(x2, p) / f(x2, p);
b3 = (x0 + x1) * (x0 * x0 + x1 * x1) - 4* x2 * x2 * x2;
z3 = x1 * x1 + x0 * x1 + x0 * x0 - 3* x2 * x2;
g3 = x1 + x0 - 2* x2 ;
a[2] = ((a2 * b1 - a1 * b2) * (z3 * b1 - z1 * b3) - (z2 * b1 - z1 * b2)
* (a3 * b1 - a1 * b3)) / ((g1 * b2 - g2 * b1) * (z1 * b3 - z3 * b1)
+ (z2 * b1 - z1 * b2) * (g1 * b3 - g3 * b1));
a[3] = (a2 * b1 - a1 * b2 + (g1 * b2 - b1 * g2) * a[2]) / (b1 * z2 - z1 * b2);
a[4] = (a1 - z1 * a[3] - g1 * a[2]) / b1;
a[1] = (1 / (x2 - x0)) * (Math::Log(f(x2, p) / f(x0, p)) - a[4] * (x2 * x2 * x2
* x2 - x0 * x0 * x0 * x0) - a[3] * (x2 * x2 * x2 - x0 * x0 * x0)
- a[2] * (x2 * x2 - x0 * x0));
a[0] = f(x0, p) * Math::Exp(-(a[1] * x0 + a[2] * x0 * x0 + a[3] * x0 * x0 * x0 + a[4] * x0 * x0 * x0 * x0));
}
///////////////////////////////////////////////////////////////////////////
void ermit_4(double *a, double x0, double x2, int p) {
double a1, a2, a3, b1, b2, b3, z1, z2, z3, g1, g2, g3;
double x1, h;
x1 = (x0 + x2) / 2;
h = x1 - x0;
a1 = (f(x2, p) - f(x0, p)) / (x2 - x0) - (f(x1, p) - f(x0, p)) / (x1 - x0);
b1 = (x2 + x0) * (x2 * x2 + x0 * x0) - (x1 + x0) * (x1 * x1 + x0 * x0);
z1 = x2 * x2 + x2 * x0 - x1 * x1 - x1 * x0;
g1 = x2 - x1;
a2 = (f(x1, p) - f(x0, p)) / (x1 - x0) - fp(x0, p);
b2 = x1 * x1 * x1 + x0 * x1 * (x0 + x1) - 3* x0 * x0 * x0;
z2 = x1 * x1 + x0 * x1 - 2* x0 * x0;
g2 = x1 - x0;
a3 = (f(x1, p) - f(x0, p)) / (x1 - x0) - fp(x2, p);
b3 = (x0 + x1) * (x0 * x0 + x1 * x1) - 4* x2 * x2 * x2;
z3 = (x1 * x1 + x0 * x1 + x0 * x0) - 3* x2 * x2;
g3 = (x1 + x0 - 2* x2 );
a[2] = ((a2 * b1 - a1 * b2) * (z3 * b1 - z1 * b3) - (z2 * b1 - z1 * b2)
* (a3 * b1 - a1 * b3)) / ((g1 * b2 - g2 * b1) * (z1 * b3 - z3 * b1)
+ (z2 * b1 - z1 * b2) * (g1 * b3 - g3 * b1));
a[3] = (a2 * b1 - a1 * b2 + (g1 * b2 - b1 * g2) * a[2]) / (b1 * z2 - z1
* b2);
a[4] = (a1 - z1 * a[3] - g1 * a[2]) / b1;
a[1] = (f(x1, p) - f(x0, p)) / h - a[2] * (x1 + x0) - a[3] * (x1 * x1 + x1
* x0 + x0 * x0) - a[4] * (x1 + x0) * (x1 * x1 + x0 * x0);
a[0] = f(x0, p) - a[1] * x0 - a[2] * x0 * x0 - a[3] * x0 * x0 * x0 - a[4]
* x0 * x0 * x0 * x0;
}
////////////////////////////////////////////////////////////////
void ermit_5(double *a, double zl, double zp, int p) {
double h, x1;
h = (zp - zl) / 2;
x1 = (zp + zl) / 2;
a[3] = ((h * h * (fp(zp, p) - fp(zl, p))) / (f(zp, p) - f(zl, p) - h * (fp(
zp, p) + fp(zl, p)))) - x1;
a[2] = ((fp(zp, p) - fp(zl, p)) * (((x1 + a[3]) * (x1 + a[3]) - h * h)
* ((x1 + a[3]) * (x1 + a[3]) - h * h))) / (4* h * (x1 + a[3]));
a[0] = fp(zl, p) + a[2] / ((x1 + a[3] - h) * (x1 + a[3] - h));
a[1] = f(zl, p) - a[0] * (x1 - h) - a[2] / (x1 - h + a[3]);
}
////////////////////////////////////////////////////////////////////
void ermit_8(double *a, double zl, double zp, int p) {
double j0, j1, j2, m0, m1;
j0 = (Math::Exp(f(zp, p)) - Math::Exp(f(zl, p))) / (zp - zl);
j1 = (zl * zl - zp * zp) / (zp - zl);
j2 = (zl * zl * zl - zp * zp * zp) / (zp - zl);
m0 = (f(zl, p) * Math::Exp(f(zl, p)) - j0) / (j1 - 2* zl );
m1 = (2* zl * zl - j2) / (j1 - 2* zl );
a[3] = (-fp(zp, p) * Math::Exp(f(zp, p)) + j0 + m0 * j1 - 2* zp * m0) / (3* zp
* zp + 2* zp * m1 - j2 - m1 * j1);
a[2] = m0 + a[3] * m1;
a[1] = j0 + j1 * a[2] + a[3] * j2;
a[0] = Math::Exp(f(zl, p)) - a[1] * zl - a[2] * zl * zl - a[3] * zl * zl * zl;
}
///////////////////////////////////////////////////////////////////
void ermit_9(double *a, double zl, double zp, int p) {
double j1, j2, j3, j4, m1, m2, m3, k1, k2, z;
z = (zp + zl) / 2;
j1 = (zp * zp - z * z) / (z - zp);
j2 = (zp * zp * zp - z * z * z) / (z - zp);
j3 = (zp * zp * zp * zp - z * z * z * z) / (z - zp);
j4 = (Math::Exp(f(z, p)) - Math::Exp(f(zp, p))) / (z - zp);
m1 = (Math::Exp(f(zp, p)) - Math::Exp(f(zl, p)) + j4 * (zl - zp)) / (zp * zp - zl * zl + j1 * (zp - zl));
m2 = (zl * zl * zl - zp * zp * zp + j2 * (zl - zp)) / (zp * zp - zl * zl
+ j1 * (zp - zl));
m3 = (zl * zl * zl * zl - zp * zp * zp * zp + j3 * (zl - zp)) / (zp * zp
- zl * zl + j1 * (zp - zl));
k1 = (Math::Exp(f(zl, p)) * fp(zl, p) - j4 - m1 * j1 - 2* zl * m1) / (j2 + 3* zl
* zl + j1 * m2 + 2* m2 * zl);
k2 = (j3 + 4* zl * zl * zl + j1 * m3 + 2* m3 * zl) / (j2 + 3* zl * zl + j1
* m2 + 2* m2 * zl);
a[4] = (Math::Exp(f(zp, p)) * fp(zp, p) - j4 - m1 - j1 - 2* zp * m1 - k1 * j2
- 3* zp * zp * k1 - k1 * j1 * m2 - 2* m2 * zp * k1) / (j3 + 4* zp
* zp * zp + j1 * m3 + 2* m3 * zp - k2 * j2 - 3* zp * zp * k2 - k2
* j1 * m2 - 2* m2 * zp * k2);
a[3] = k1 - k2 * a[4];
a[2] = m1 + a[3] * m2 + a[4] * m3;
a[1] = j4 + a[2] * j1 + a[3] * j2 + a[4] * j3;
a[0] = Math::Exp(f(zl, p)) - a[1] * zl - a[2] * zl * zl - a[3] * zl * zl * zl
- a[4] * zl * zl * zl * zl;
}
///////////////////////////////////////////////////////////////////
double poldiv_p3(double*a, double zl, double b1, int n, int p) {
double zp, ny, x, nyu,ny1,ny2, x1, x2;
textBox2->Text="";
nyu=Double::Parse(textBox1->Text);
String ^ path = Path::GetFileName("rez.txt");
FileInfo^ fi = gcnew FileInfo(path);
StreamWriter ^ sw = fi->CreateText();
int l = 0;
double t,ch1,ch2,ch3;
chart1->Series["Function"]->Points->Clear();
chart1->Series["Spline"]->Points->Clear();
chart2->Series["error"]->Points->Clear();
zp = zl + 0.00510101101;;
while (1) {
do {
zp += 0.000135110101101;
if (zp > b1) {
zp = b1;
if (s1->Checked == true) {
ermit_1(a, zl, zp, p);
}
if (s2->Checked == true) {
ermit_2(a, zl, zp, p);
}
if (s3->Checked == true) {
ermit_3(a, zl, zp, p);
}
if (s4->Checked == true) {
ermit_4(a, zl, zp, p);
}
if (s5->Checked == true) {
ermit_5(a, zl, zp, p);
}
if (s6->Checked == true) {
ermit_6(a, zl, zp, p);
}
if (s7->Checked == true) {
ermit_8(a, zl, zp, p);
}
if (s8->Checked == true) {
ermit_9(a, zl, zp, p);
}
if (s9->Checked == true) {
ermit_7(a, zl, zp, p);
}
if(p==1){
x = (zl + zp) / 2;
}
if(p==2){
x1 = zl+(zp - zl) / 4;
x2 = zl+2.5*(zp - zl) / 4;
ny1=epx_p(a, x1, p);
ny2=epx_p(a, x2, p);
if(ny2>ny1){
x=x2;
}
else{x=x1;}
}
l++;
//fprint(a, zl, zp, n, ny, l);
//print(a, zl, zp, n, ny, l);
sw->WriteLine("{0:D} - ланка \n",l);
sw->WriteLine("a[0] = {0,7:e}\n", a[0]);
sw->WriteLine("a[1] = {0,7:e}\n", a[1]);
sw->WriteLine("a[2] = {0,7:e}\n", a[2]);
sw->WriteLine("a[3] = {0,7:e}\n", a[3]);
if (n == 5) {
sw->WriteLine("a[4] = {0,7:e}\n", a[4]);
}
sw->WriteLine("Ліва межа інтервалу = {0,7:e}\n", zl);
sw->WriteLine("Права межа інтервалу = {0,7:e}\n", zp);
sw->WriteLine("Похибка = {0,7:e}\n", ny);
sw->Write(sw->NewLine);
sw->Close();
for(t = zl; t <= zp; t += 0.01)
{
ch1 = f(t,p);
ch2 = sp(a,t);
ch3 = epx_p(a,t,1);
if(nyu=0.001){
if(ch3>nyu-0.00008){ch3-=0.000015;}
}
chart1->Series["Function"]->Points->AddXY(t, ch1);
chart1->Series["Spline"]->Points->AddXY(t, ch2);
chart2->Series["error"]->Points->AddXY(t, ch3);
}
return zp;
}// po if(zp > b1)
//z = (zp + ozp) / 2;
if (s1->Checked == true) {
ermit_1(a, zl, zp, p);
}
if (s2->Checked == true) {
ermit_2(a, zl, zp, p);
}
if (s3->Checked == true) {
ermit_3(a, zl, zp, p);
}
if (s4->Checked == true) {
ermit_4(a, zl, zp, p);
}
if (s5->Checked == true) {
ermit_5(a, zl, zp, p);
}
if (s6->Checked == true) {
ermit_6(a, zl, zp, p);
}
if (s7->Checked == true) {
ermit_8(a, zl, zp, p);
}
if (s8->Checked == true) {
ermit_9(a, zl, zp, p);
}
if (s9->Checked == true) {
ermit_7(a, zl, zp, p);
}
if(p==1){
x = (zl + zp) / 2;
}
if(p==2){
x1 = zl+(zp - zl) / 4;
x2 = zl+3*(zp - zl) / 4;
ny1=epx_p(a, x1, p);
ny2=epx_p(a, x2, p);
if(ny2>ny1){
x=x2;
}
else{x=x1;}
}
ny = epx_p(a, x, p);
//std::cout << "\n" << ny << " - " << nyu << "\t" << ny - nyu << "\n";
//ny=Math::Abs(f(x, p) - sp(a, x))/f(x,p)*100;
//nyu=(nyu/f(x,p))*100;
if(ny>nyu){
zp =zp- 0.000135110101101-(0.000135110101101)/2;
}
if (((nyu-ny)*100 < 0.0005)&&(nyu>ny)) {
break;
}
} while (1);
l++;
//fprint(a, zl, zp, n, ny, l);
//print(a, zl, zp, n, ny, l);
sw->WriteLine("{0:D} - ланка \n",l);
sw->WriteLine("a[0] = {0,7:e}\n", a[0]);
sw->WriteLine("a[1] = {0,7:e}\n", a[1]);
sw->WriteLine("a[2] = {0,7:e}\n", a[2]);
sw->WriteLine("a[3] = {0,7:e}\n", a[3]);
if (n == 5) {
sw->WriteLine("a[4] = {0,7:e}\n", a[4]);
}
sw->WriteLine("Ліва межа інтервалу = {0,7:e}\n", zl);
sw->WriteLine("Права межа інтервалу = {0,7:e}\n", zp);
sw->WriteLine("Похибка = {0,7:e}\n", ny);
sw->Write(sw->NewLine);
for(t = zl; t <= zp; t += 0.01)
{
ch1 = f(t,p);
ch2 = sp(a,t);
ch3 = epx_p(a,t,1);
if(nyu=0.001){
if(ch3>nyu-0.00008){ch3-=0.000015;}
}
chart1->Series["Function"]->Points->AddXY(t, ch1);
chart1->Series["Spline"]->Points->AddXY(t, ch2);
chart2->Series["error"]->Points->AddXY(t, ch3);
}
zl = zp;
zp += 0.000135110101101;
}
sw->Write(sw->NewLine);
sw->Close();
for(t = zl; t <= zp; t += 0.01)
{
ch1 = f(t,p);
ch2 = sp(a,t);
ch3 = epx_p(a,t,1);
if(nyu=0.001){
if(ch3>nyu-0.00008){ch3-=0.000015;}
}
chart1->Series["Function"]->Points->AddXY(t, ch1);
chart1->Series["Spline"]->Points->AddXY(t, ch2);
chart2->Series["error"]->Points->AddXY(t, ch3);
}
return zp;
}
//***************************************************************************void algo_p3(double*a, double zl, double b1, int n, int p) {
double X, Y, eps, nyu, x, x1, x0, zp, xx, zz,ny,dz;
nyu=Double::Parse(textBox1->Text);
String ^ path = Path::GetFileName("rez.txt");
FileInfo^ fi = gcnew FileInfo(path);
StreamWriter ^ sw = fi->CreateText();
int l = 0;
double t,ch1,ch2,ch3;
chart1->Series["Function"]->Points->Clear();
chart1->Series["Spline"]->Points->Clear();
chart2->Series["error"]->Points->Clear();
x0 = 0.1;
//zz = zp =
x1 = 0.5;
//xx =
x = 0.3;
eps = 0.00001;
nyu = 0.001;
int j = 0;
do {
Y = (f2dx(x, x1, x0, p) * ff1(x, x1, x0, p) - ff2(x, x1, x0, nyu, p)
* f1dx(x, x1, x0, p)) / (f2dy(x, x1, x0, p)
* f1dx(x, x1, x0, p) - f2dx(x, x1, x0, p) * f1dy(x, x1, x0, p));
X = (-ff1(x, x1, x0, p) - f1dy(x, x1, x0, p) * Y) / f1dx(x, x1, x0, p);
x += X;
x1 += Y;
} while ((Math::Abs(ff1(x, x1, x0, p)) >= eps) && (Math::Abs(ff2(x, x1, x0, nyu, p)) >= eps));
sw->WriteLine("{0:D} - ланка \n",l);
sw->WriteLine("a[0] = {0,7:e}\n", a[0]);
sw->WriteLine("a[1] = {0,7:e}\n", a[1]);
sw->WriteLine("a[2] = {0,7:e}\n", a[2]);
sw->WriteLine("a[3] = {0,7:e}\n", a[3]);
if (n == 5) {
sw->WriteLine("a[4] = {0,7:e}\n", a[4]);
}
sw->WriteLine("Ліва межа інтервалу = {0,7:e}\n", zl);
sw->WriteLine("Права межа інтервалу = {0,7:e}\n", zp);
sw->WriteLine("Похибка = {0,7:e}\n", ny);
sw->Write(sw->NewLine);
for(t = zl; t <= zp; t += 0.01)
{
ch1 = f(t,p);
ch2 = sp(a,t);
ch3 = epx_p(a,t,1);
chart1->Series["Function"]->Points->AddXY(t, ch1);
chart1->Series["Spline"]->Points->AddXY(t, ch2);
chart2->Series["error"]->Points->AddXY(t, ch3);
}
zl = zp;
zp += dz;}
Результати роботи програми
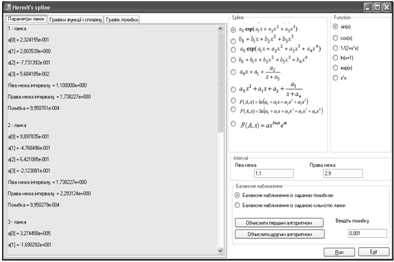
Рис. 1. Параметри ланок сплайна![]()
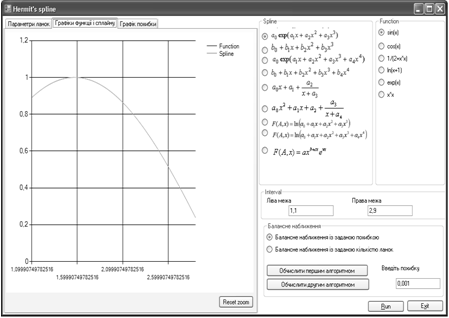
Рис. 2. Графік сплайна і функції ![]() .
.
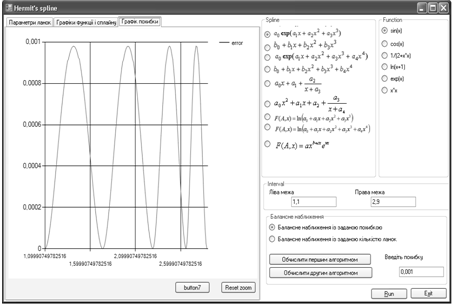
Рис. 3. Графік похибки наближення функції ![]()
0 комментариев