Навигация
Сообщение темы и целей урока
70672
знака
3
таблицы
3
изображения
1. Сообщение темы и целей урока.
2. Работа по теме урока.
Линейное уравнение 
с 2 переменными 
и 
всегда можно преобразовать к виду 
, где 
-числа (коэффициенты), причем 
.
Этот частный вид линейного уравнения будем называть линейной функцией.
-независимая переменная (или аргумент), -зависимая переменная.
Линейная функция - это специальный вид линейного уравнения с 2 переменными.
Графиком линейной функции является прямая.
3. Исторический экскурс о Пьере Ферма.
Пьер Ферма (1601-1665)
В истории математики Пьер Ферма занимает особое место. Он известен как автор "великой теоремы Ферма", которая чрезвычайно просто формулируется и которую до сих пор еще не удалось доказать.
Сумма квадратов двух целых чисел снова может быть квадратом целого числа. Например, 52+122=132. Теорема Ферма утверждает, что для более высоких степеней подобное невозможно, т.е. уравнение хn+yn=zn не имеет решений в целых числах ни при каких n > 2.
Сотни квалифицированных математиков и тысячи дилетантов в течение трехсот лет пытались доказать эту теорему. В 1993 году на страницах многих газет, не склонных писать о математике, промелькнула сенсационная новость: теорема наконец-то доказана! Но вскоре, как бывало уже не раз, в доказательстве обнаружилась ошибка.
Ферма вошел в славную когорту "обыкновенных гениев" начала XVII века, вместе с Декартом, Паскалем, Гюйгенсом… Но, справедливости ради, надо отметить, что именно его долгое время считали сильнейшим математиком века - вплоть до появления работ Ньютона и Лейбница.
Как и Декарт, Пьер Ферма родился на юге Франции, получил всестороннее образование - не только естественнонаучное, но и гуманитарное. Большую часть жизни он проработал юристом в парламенте города Тулузы. Хотя в то время математика уже была уважаемой наукой, но еще не считалась профессией.
Научных журналов тоже еще не существовало (первый из них появился в год смерти Ферма). Поэтому математики обменивались сведениями о своих достижениях в личной переписке. В истории науки вошло имя парижского священника Мерсенна, сыгравшего роль информационного центра для математиков разных стран. Сообщить о своем открытии Мерсенну означало опубликовать его для всей Европы.
В 1636 году Ферма отправил Мерсенну письмо, в котором изложил свой метод решения задач о максимуме и минимуме. Мерсенн переслал копию этого письма другим математикам, в том числе Декарту. Рассуждения Ферма, использующие бесконечно малые величины, показались Декарту недостаточно ясными, и он подверг работу младшего коллеги резкой критике. Так через две тысячи лет после работ Архимеда возобновились споры о законности действий с бесконечно малыми величинами, не утихавшие до XIX столетия.
Одновременно с Декартом Ферма пришел к созданию аналитической геометрии - науки, описывающей геометрические фигуры при помощи координат и формул. Однако Ферма пользовался неудобными обозначениями и не претендовал на открытие "универсальной математики", поэтому его рукопись была менее известна, чем "Геометрия" Декарта.
Ферма был одним из отцов теории вероятностей - современной науки, без которой невозможна работа страховых компаний или расчеты мощностей телефонных станций. Поводом для его исследований были азартные игры, особенно игра в кости, весьма распространенная в то время.
Помимо всего этого, Ферма оказался единственным математиком XVII века, занимавшимся арифметикой. Именно с его работ начинается современная теория чисел. Настольной книгой Ферма стала "Арифметика" древнегреческого математика Диофанта.
Самостоятельная работа учащихся: подготовить сообщение о Паскале.
4. Закрепление полученных знаний.
4.1 Выполнение № 897 (у доски):
а) Заданный промежуток является интервалом 
наибольшего и наименьшего значений не существует.
б) Функция убывает наибольшее значение в начале промежутка, а наименьшее в конце. Но в конце промежутка стоит знак +∞ наименьшего значения не существует.
Наибольшее 
в) Функция возрастает наименьшее значение в начале промежутка, а наибольшее в конце.
Наименьшее 
Наибольшее =
г) Функция возрастает наименьшее значение в начале промежутка, а наибольшее в конце.
Но в начале промежутка стоит знак - ∞ наименьшего значения не существует.
Наибольшее 
4.2 Выполнение № 898 (а) (у доски):
а) Функция возрастает наименьшее значение в начале промежутка, а а наибольшее в конце.
Наименьшее 
Наибольшее 
4.3 Выполнение № 863 (г) (у доски):
г) 
|
| -1 | 0 | 1 |
|
| -1 | 1 | 3 |
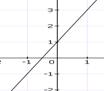
4.4 Выполнение № 855 (б) (с комментированием):
б) 
4.5 Выполнение № 851 (а) (с комментированием):
а) 
Похожие работы
... но все они сходятся в одном, что игра является способом развития личности, обогащения ее жизненного опыта. - Из всего многообразия игр можно выделить математическую игру, как средство развития познавательного интереса учащихся к математике. Использование математической игры во внеклассной работе по математике наиболее эффективно способствует возникновению интереса у учащихся к математике. - ...
... и только затем ознакомьтесь с ходом решения, предлагаемым Е. И. Игнатьевым. Данный ход решения можно применять в начальной школе с использованием иллюстративного материала, что с большей степенью повысит эффективность развития познавательной активности младших школьников. «Решение: Ясно, что приходится начать с козы. Крестьянин, перевезши козу, возвращается и берет волка, которого перевозит на ...
... , которая призвана возбудить интерес к учению, сделать учение увлекательным, мобилизировать психологическую энергию и усилия, поддержать стремления, преумножить любознательность и старания. Мотивы и стимулы в учебной деятельности школьников долгое время находились как бы на периферии педагогических исследований. Большую помощь в разработке этой проблемы оказали психологи. Однако, с конца 70-х гг. ...
... Владимир Ильич625000 Тюмень, ул. Советская 88-1 Хабаровский государственный педагогический университет На правах рукописи Золотарева Светлана Алексеевна Развитие Теории урока в советской дидактике периода середины 50-х – середины 60-х годов Диссертация на соискание ученой степеникандидата педагогических наук. 13.00.01 – Общая педагогика. Научный руководитель: доктор ...
0 комментариев