Навигация
Разработка программы факультативного курса по теории вероятностей в курсе математики 8 класса
ГОУ СПО «Кунгурское педагогическое училище»
ПЦК преподавателей естественно-математических дисциплин
Разработка программы факультативного курса по теории вероятностей в курсе математики 8 класса
Допущена к защите
Зам. Директора по учебной работе
Л.А. Патракова, 2009 г.
Председатель ПЦК
естественно-математических дисциплин
Т.А. Трясцына, 2009 г.
Выпускная квалификационная работа
по методике преподавания математики
Михайловой Натальи Анатольевны
специальность 050201 математика группа М-51
отделение: заочное
Руководитель: Янкина Л.Г.,
преподаватель математики
Защита состоялась:
2009
Оглавление
Введение
1. Предмет теории вероятностей
1.1 Основные понятия
1.2 Правила и теоремы теории вероятностей
2. Разработка программы факультативного курса по теории вероятностей в курсе математики 8 класса
2.1 Основные понятия о факультативном курсе
2.2 Методика преподавания теории вероятностей
Заключение
Литература
Приложения
Введение
Теория вероятностей является одним из классических разделов математики. Она имеет длительную историю. Основы этого раздела науки были заложены великими математиками. Назову, например, Ферма, Бернулли, Паскаля. Позднее развитие теории вероятностей определились в работах многих ученых. Большой вклад в теорию вероятностей внесли ученые нашей страны: П.Л. Чебышев, А.М. Ляпунов, А.А. Марков, А.Н. Колмогоров. По словам Б.В. Гнеденко: «Теория вероятностей, подобно другим разделам математики, развилась из потребностей практики; в абстрактной форме она отражает закономерности, присущие случайным событиям массового характера».
Теория вероятностей используется в физике, технике, экономке, биологии и медицине. Особенно возросла ее роль в связи с развитием вычислительной техники.
Например, при бросании монеты нельзя предсказать, какой стороной она упадет, для этого необходимо было бы учесть слишком много различных факторов: работу мышц руки, участвующей в бросании, малейшие отклонения в распределении массы монеты, движение воздуха и т.д. Результат бросания монеты случаен. Но, оказывается, при достаточно большом числе бросаний монеты существует определенная закономерность (герб и цифра выпадут приблизительно поровну).
Закономерности, которым подчиняются случайные события, изучаются в разделах математики, которые называются теорией вероятности.
Можно привести много других примеров случайных величин. Все же и в мире случайностей обнаруживаются определенные закономерности. Математический аппарат для изучения таких закономерностей и дает теория вероятностей. Таким образом, теория вероятностей занимается математическим анализом случайных событий и связанных с ними случайных величин.
В настоящее время теория вероятностей завоевала очень серьезное место в науке и прикладной деятельности. Ее идеи, метода и результаты не только используются, но буквально пронизывают все естественные и технические науки, экономику, планирование, организацию производства, связи, а также такие далекие, казалось бы, от математики науки, как лингвистику и археологию. Сейчас без достаточно развитых представлений о случайных событиях и их вероятностях, без хорошего представления о том, что явления и процессы, с которыми мы имеем дело, подчиняются более сложным закономерностям, невозможно полноценно работать в физике, химии, биологии, управлять производственными процессами. А, следовательно, данная тема актуальна и нуждается в рассмотрении.
Однако теория вероятностей почти не рассматривается в школьном курсе математики, так как в учебниках очень мало заданий. Зато на различных олимпиадах такие задания встречаются часто. Решением данной проблемы может служить создание факультативного курса по теории вероятностей.
Цель: разработать программу факультативного курса по теории вероятностей в курсе математики 8 класса.
Задачи:
· Изучить методическую и научную литературу по теме;
· Показать методику работы при использовании элементов теории вероятностей на уроках математики в школе;
· Подобрать систему задач и упражнений, направленных на изучение данной темы.
Объект исследования - процесс подготовки учителя к обучению школьников элементам теории вероятностей.
Предмет исследования - влияние системы задач на формирование вероятностных понятий у учеников 8 класса.
Контингент – ученики 8-го класса.
1. Предмет теории вероятностей 1.1 Основные понятия
Теория вероятностей возникла в середине XVII в. Первые работы по теории вероятностей, принадлежащие французским учёным Б. Паскалю и П. Ферма и голландскому учёному X. Гюйгенсу, появились в связи с подсчётом различных вероятностей в азартных играх. Крупный успех теории вероятностей связан с именем швейцарского математика Я. Бернулли, установившего закон больших чисел для схемы независимых испытаний с двумя исходами (опубликовано в 1713).
Следующий (второй) период истории теории вероятностей (XVIII в., начало XIX в.) связан с именами А. Муавра (Англия), П. Лапласа (Франция), К. Гаусса (Германия) и С. Пуассона (Франция). Это - период, когда теория вероятностей уже находит ряд весьма актуальных применений в естествознании и технике (главным образом в теории ошибок наблюдений, развившейся в связи с потребностями геодезии и астрономии, и в теории стрельбы). К этому периоду относится доказательство первых предельных теорем, носящих теперь названия теорем Лапласа (1812) и Пуассона (1837); А. Лежандром (Франция, 1806) и Гауссом (1808) в это же время был разработан способ наименьших квадратов.
Третий период истории теории вероятностей. (2-я половина XIX в.) связан в основном с именами русских математиков П.Л. Чебышева, А.М. Ляпунова и А.А. Маркова (старшего). Теория вероятностей развивалась в России и раньше. В XVIII в. ряд трудов был написан работавшими в России Л. Эйлером, Н. Бернулли и Д. Бернулли. Во второй период развития теории вероятностей следует отметить работы М.В. Остроградского по вопросам теории вероятностей, связанным с математической статистикой, и В.Я. Буняковского по применениям теории вероятностей к страховому делу, статистике и демографии. Со 2-й половины XIX в. исследования по теории вероятностей в России занимают ведущее место в мире. Чебышев и его ученики Ляпунов и Марков поставили и решили ряд общих задач в теории вероятностей, обобщающих теоремы Бернулли и Лапласа. Чебышев чрезвычайно просто доказал (1867) закон больших чисел при весьма общих предположениях. Он же впервые сформулировал (1887) центральную предельную теорему для сумм независимых случайных величин и указал один из методов её доказательства. Другим методом Ляпунов получил (1901) близкое к окончательному решение этого вопроса. Марков впервые рассмотрел (1907) один случай зависимых испытаний, который впоследствии получил название цепей Маркова.
В Западной Европе во 2-й половине XIX в. получили большое развитие работы по математической статистике (в Бельгии - А. Кетле, в Англии - Ф. Гальтон) и статистической физике (в Австрии - Л. Больцман). Которые наряду с основными теоретическими работами Чебышева, Ляпунова и Маркова создали основу для существенного расширения проблематики теории вероятностей в четвёртом (современном) периоде её развития. Этот период истории теории вероятностей характеризуется чрезвычайным расширением круга её применений, созданием нескольких систем безукоризненно строгого математического обоснования теории вероятностей, новых мощных методов, требующих иногда применения (помимо классического анализа) средств теории множеств, теории функций действительного переменного и функционального анализа. В этот период советская наука продолжает занимать значительное, а в ряде направлений и ведущее положение. В нашей стране новый период развития теории вероятностей открывается деятельностью С. Н. Бернштейна, значительно обобщившего классические предельные теоремы Чебышева, Ляпунова и Маркова и впервые в России широко поставившего работу по применениям теории вероятностей к естествознанию. Позднее (в 30-х гг.) они и Е.Е. Слуцкий заложили основы теории случайных процессов. В. И. Романовский Ташкент и Н. В. Смирнов Москва поставили на большую высоту работу по применениям теории вероятностей к математической статистике [12].
Теория вероятностей изучает закономерности случайных явлений. Она применяется в физике и других разделах естествознания, в экономике, в военном деле, в разнообразных технических дисциплинах и во многих других областях человеческой деятельности.
В последние десятилетия теория вероятностей все глубже проникает в гуманитарные науки. На ней основываются статистические методы, необходимые для работы лингвистов и психологов, социологов и политологов. Знание теории вероятностей необходимо теперь каждому экспериментатору, так как она указывает способы обработки результатов эксперимента, дает рекомендации по его планированию [13]. Поэтому, сейчас так актуально изучать данный раздел математики. Его основа – случайные события.
Случайности подстерегают нас на каждом шагу. Случай поворачивается к человеку своими разными сторонами. Случайность – это прежде всего непредсказуемость, которая является результатом нашего незнания, нашей слабой осведомленности, результатом отсутствия необходимой информации.
С помощью данной работы попытаемся открыть для себя вероятностную природу окружающего нас мира, познакомимся со случайными явлениями, попробуем ориентироваться в мире случайности, используя его величество случай.
Понятие о случайном событии
Опыт, эксперимент, наблюдение явления называется испытанием. Испытаниями являются: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесенными на каждую грань числом очков - от одного до шести).
Результат, исход испытания, называется событием. Событиями являются выпадение герба или цифры, попадание в цель или промах, появление того или иного числа очков на брошенной игральной кости. Для обозначения событий используют большие буквы латинского алфавита: А,В, С и т.д.
Два события называют совместимыми, если появление одного из них не исключает появления другого в одном и том же испытании.
Испытание - однократное бросание игральной кости. Событие А - появление четырех очков. Событие В - появление четного числа очков. События А и В совместимые.
Два события называют несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании.
Испытание - однократное бросание монеты. Событие А - выпадение герба, событие В - выпадение цифры. Эти события несовместимы, так как появление одного из них исключает появление другого.
Несовместимость более чем двух событий означает их попарную несовместимость.
Испытание - однократное бросание игральной кости. Пусть события А1 , А2 , А3, А4 , А5 , А6, - соответственно выпадение одного очка, двух, трех и т.д. Эти события являются несовместимыми.
Два события А и В называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит. Событие, противоположное событию А, обозначают через![]() .
.
Испытание - бросание монеты. Событие А - выпадение герба, событие В - выпадение цифры. Эти события противоположны, так как исходами бросания могут быть лишь они, и появление одного из них исключает появление другого, т.е.
А = ![]()
![]() или
или ![]() = В.
= В.
Событие называют достоверным, если в данном испытании оно является единственно возможным его исходом, и невозможным, если в данном испытании оно заведомо не может произойти. Испытание - извлечение шара из урны, в которой все шары белые. Событие А - вынут белый шар - достоверное событие; событие В - вынут черный шар - невозможное событие.
Достоверное и невозможное события в данном испытании являются противоположными.
Событие А называют случайным, если оно объективно может наступить или не наступить в данном испытании.
Событие А6 - выпадение шести очков при бросании игральной кости - случайное. Оно может наступить, но может и не наступить в данном испытании.
Всякое испытание влечет за собой некоторую совокупность исходов - результатов испытания, т.е. событий. Во многих случаях возможно перечислить все события, которые могут быть исходами данного испытания.
Классическое определение вероятности
Говорят, что совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится хотя бы одно из них.
Примеры полных групп событий: выпадение герба и выпадение цифры при одном бросании монеты; попадание в цель и промах при одном выстреле; выпадение одного, двух, трех, четырех, пяти и шести очков при одном бросании игральной кости.
Рассмотрим полную группу попарно несовместимых событий U1, U2, ., Un, связанную с некоторым испытанием. Предположим, что в этом испытании осуществление каждого из событий ![]() , (i = 1,2, ..., n) равновозможное, т.е. условия испытания не создают преимущества в появлении какого-либо события перед другими возможными.
, (i = 1,2, ..., n) равновозможное, т.е. условия испытания не создают преимущества в появлении какого-либо события перед другими возможными.
![]()
![]()
![]() События U1, U2,..., Un, образующие полную группу попарно несовместимых и равновозможных событий, называется элементарными событиями.
События U1, U2,..., Un, образующие полную группу попарно несовместимых и равновозможных событий, называется элементарными событиями.
Вернемся к опыту с подбрасыванием игральной кости. Пусть ![]() - событие, состоящее в том, что кость выпала гранью с цифрой 1. События U1 , U2, ... , U6 образуют полную группу попарно несовместимых событий. Так как кость предполагается однородной и симметричной, то события U1 , U2,... , U6 являются и равновозможными, т.е. элементарными.
- событие, состоящее в том, что кость выпала гранью с цифрой 1. События U1 , U2, ... , U6 образуют полную группу попарно несовместимых событий. Так как кость предполагается однородной и симметричной, то события U1 , U2,... , U6 являются и равновозможными, т.е. элементарными.
Событие А называют благоприятствующим событию В, если наступление события А влечет за собой наступление события В.
Пусть при бросании игральной кости события U2, U4, и U6 -появление соответственно двух, четырех и шести очков и А - событие, состоящее в появлении четного числа очков; события U2, U4 и U6 благоприятствуют событию А.
Вероятностью Р(А) события А называют отношение ![]() числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т.е.
числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т.е.
Р(А)= ![]() .
.
Вычислим вероятность выпадения герба при одном бросании монеты. Очевидно, событие А - выпадение герба и событие В — выпадение цифры образуют полную группу несовместимых и равновозможных событий для данного испытания. Значит, здесь n = 2. Событию А благоприятствует лишь одно событие - само А, т.е. здесь m = 1. Поэтому
Р(А) =![]() .
.
Найти вероятность того, что при бросании игральной кости выпадет число очков, делящееся на 2 (событие А).
Число элементарных событий здесь 6. Число благоприятствующих элементарных событий 3 (выпадение 2, 4 и 6). Поэтому Р(А)=![]() =
= ![]() .
.
Из приведенного классического определения вероятности вытекают следующие ее свойства [1, 510].
Свойства классического определения вероятности
1. Вероятность достоверного события равна единице. Действительно, достоверному событию должны благоприятствовать все n элементарных событий, т.е. m = n и, следовательно,
Р(А)= ![]() =
=![]() =1.
=1.
2. Вероятность невозможного события равна нулю. В самом деле, невозможному событию не может благоприятствовать ни одно из элементарных событий, т.е. m = 0, откуда
Р(А)= ![]() =
=![]() =0.
=0.
Похожие работы
... обучения, школа предоставляет учащимся право выбора предметов по интересам и склонностям. В соответствии с требованиями была разработана программа факультативного курса по теме «Элементы комбинаторики» для 8 класса. 2.2 Программа факультативного курса Пояснительная записка В математике и ее приложениях часто приходится иметь дело с различного рода множествами и подмножествами: ...
... способом аналитико – синтетический метод применяется на тех – же решениях. Единственное различие состоит в том , что на этапе поиска решения применяется анализ в нисходящей форме. Методика обучения решения технических задач. Математические задачи, в которых есть хотя бы один объект, являющийся реальным предметом, принято называть текстовыми (сюжетными, практическими, арифметическими и т.д) ...
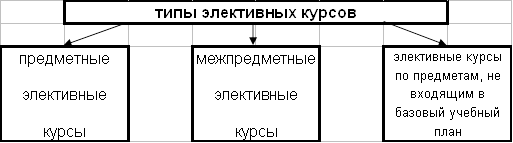
... -иллюстративного и репродуктивного метолов, а экономический профиль ориентирован на формирование прикладного стиля мышления. 2. Методика проведения элективных курсов по математике в профильной школе 2.1 Цели организации элективных курсов по математике Принципиальным положением организации школьного математического образования в настоящее время является дифференциация обучения ...
... при ошибке в его выборе, учитывать по уровневый подход. 4. Математика должна входить в набор обязательных учебных предметов любого из профилей.2 МАТЕМАТИЧЕСКИЙ ФАКУЛЬТАТИВ КАК ВЕДУЩАЯ ФОРМА ПРОФИЛЬНОГО ОБУЧЕНИЯ МАТЕМАТИКЕ В ОБЩЕОБРАЗОВАТЕЛЬНОЙ ШКОЛЕ2.1. Организационно-педагогические условия успешного функционирования математических факультативов Еще на рубеже XIX и XX вв. некоторые ...

0 комментариев