Навигация
Вероятность случайного события есть положительное число, заключенное между нулем и единицей
3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных событий. Поэтому в этом случае 0 < m < n и, значит, 0 < ![]() < 1. Следовательно, 0 < Р(А) < 1.
< 1. Следовательно, 0 < Р(А) < 1.
Итак, вероятность любого события удовлетворяет двойному неравенству, 0 ![]() Р(А)
Р(А)![]() 1 [2, 17].
1 [2, 17].
Статистическое определение вероятности
Классическое определение вероятности не является пригодным для изучения произвольных случайных событий. Так, оно неприемлемо, если результаты испытания не равновозможны. Например, при бросании неправильной игральной кости выпадение ее различных граней не равновозможно.
В таких случаях используется, так называемое, статистическое определение вероятности.
Пусть произведено n испытаний, при этом некоторое событие А наступило m раз (m < n).
Число m называют абсолютной частотой (или просто частотой) события А, а отношение Р*(А) = ![]() называют относительной частотой события А.
называют относительной частотой события А.
При транспортировке из 10 000 арбузов испортилось 26. Здесь m = 26 - абсолютная частота испорченных арбузов, а Р*(А) = ![]() = 0,0026 - относительная.
= 0,0026 - относительная.
Результаты многочисленных опытов и наблюдений помогают заключить: при проведении серий из n испытаний, когда число сравнительно мало, относительная частота Р*(А) принимает значения, которые могут довольно сильно отличаться друг от друга. Но с увеличением n - числа испытаний в сериях – относительная частота Р*(А) =![]() приближается к некоторому числу Р(А), стабилизируясь возле него и принимая все более устойчивые значения.
приближается к некоторому числу Р(А), стабилизируясь возле него и принимая все более устойчивые значения.
Было проведено 10 серий бросаний монеты, по 1000 бросаний в каждой. Относительные частоты выпадения герба оказались равными 0,501 0,485; 0,509; 0,536; 0,485; 0,488; 0,500; 0,497; 0,494; 0,484. Эти частота группируются около числа 0,5.
По официальным данным шведской статистики относительные частоты рождения девочек по месяцам 1935 г. характеризуются следующими числами (расположены в порядке следования месяцев, начиная с января): 0,486; 0,489; 0,490; 0,471; 0,478; 0,482; 0,462; 0,484; 0,485; 0,491; 0,482; 0,47. Эти частоты группируются около числа 0,482.
Относительная частота события приближенно совпадает с его вероятностью, если число испытаний достаточна велико. Имеется огромный опытный материал по проверке последнего утверждения. Укажем еще один такой пример с бросанием монеты (приложение 1).
Здесь относительные частоты незначительно отклоняются от числа 0,5, причем тем меньше, чем больше число испытаний. При 4040 испытаниях отклонение равно 0,008, а при 24 000 - 0,0005.
Таких примеров очень много. Возникли целые науки о том, как же эффективно действовать в нашем случайном мире. Их задачей является уменьшение неприятностей от случайного при использовании самой случайности.
Таким образом, было рассмотрено два определения теории вероятностей: классическое и статистическое [6, 210].
Для решения задач по данной теме необходимо использовать основные правила и теоремы теории вероятности.
1.2 Правила и теоремы теории вероятностей
Теорема сложения вероятностей несовместимых событий
Суммой событий А и В называют событие С = А + В, состоящее в наступлении, по крайней мере, одного из событий А или В.
Испытание - стрельба двух стрелков (каждый делает по одному выстрелу). Событие А - попадание в мишень первым стрелком, событие В - попадание в мишень вторым стрелком. Суммой событий А и В будет событие С = А + В, состоящее в попадании в мишень, по крайней мере, одним стрелком.
Аналогично суммой конечного числа событий А1 , А2, ..., Аk называют событие А = А1 + А2 + … + Аk, состоящее в наступлении хотя бы одного из событий Ai (i = 1,..., k).
Произведением событий А и В называют событие С = АВ, состоящее в том, что в результате испытания произошло и событие А и событие В.
Аналогично произведением конечного числа событий А1 , А2, ..., Аk называют событие А = А1 А2 … Аk, , состоящее в том, что в результате испытания произошли все указанные события.
В условиях предыдущего примера произведением событий А и В будет событие С = АВ, состоящее в попадании в мишень двух стрелков.
Из определения непосредственно следует, что АВ = ВА.
Теорема. Вероятность суммы двух несовместимых событий А и В равна сумме вероятностей этих событий:
Р(А+В)=Р(А)+Р(В). (1)
Доказательство. Используем классическое определение вероятности. Предположим, что в данном испытании число всех элементарных событий равно n, событию А благоприятствуют k элементарных событий, событию В - I элементарных событий. Так как А и В - несовместимые события, то ни одно из элементарных событий U1 , U2,... , Un не может одновременно благоприятствовать и событию А и событию В. Следовательно, событию А + В будет благоприятствовать k + l элементарных событий. По определению вероятности Р(А)=![]() , Р(В)=
, Р(В)=![]() , Р(А+В)=
, Р(А+В)= ![]() откуда и следует утверждение теоремы.
откуда и следует утверждение теоремы.
Совершенно так же теорема формулируется и доказывается для любого конечного числа попарно несовместимых событий.
Следствие. Сумма вероятностей противоположных событий А и![]() равна единице:
равна единице:
Р(А)+Р(![]() )= 1
)= 1
Так как события А и![]() несовместимы, то по доказанной выше теореме Р(А) + Р(
несовместимы, то по доказанной выше теореме Р(А) + Р(![]() ) = Р (А +
) = Р (А +![]() ). Событие А +
). Событие А + ![]() есть достоверное событие (ибо одно из событий А или
есть достоверное событие (ибо одно из событий А или ![]() произойдет). Поэтому Р (А +
произойдет). Поэтому Р (А +![]() ) =1.
) =1.
В урне 10 шаров: 3 красных, 5 синих и 2 белых. Какова вероятность вынуть цветной шар, если вынимается один шар? Вероятность вынуть красный шар Р(А) =![]() , синий Р(В) =
, синий Р(В) =![]() . Так как события А и В несовместимы, то по доказанной выше теореме
. Так как события А и В несовместимы, то по доказанной выше теореме
Р(А + В)= Р(А) + Р(В) = ![]() +
+![]() = 0,8 [3, 25].
= 0,8 [3, 25].
Теорема умножения вероятностей
Два события А и В называют независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события А и В называют зависимыми [5, 19].
Пример 1. Пусть в урне находятся 2 белых и 2 черных шара. Пусть событие А - вынут белый шар. Очевидно, Р(А) =![]() . После первого испытания
вынутый шар кладется обратно в урну, шары перемешиваются и снова вынимается шар. Событие В - во втором испытании вынут белый шар – также имеет вероятность Р(В) =
. После первого испытания
вынутый шар кладется обратно в урну, шары перемешиваются и снова вынимается шар. Событие В - во втором испытании вынут белый шар – также имеет вероятность Р(В) =![]() , т.е. события А и В- независимые.
, т.е. события А и В- независимые.
Предположим теперь, что вынутый шар в первом испытании не кладется обратно в урну. Тогда если произошло событие А, т.е. в первом испытании вынут белый шар, то вероятность события В уменьшается Р(В) =![]() ,если в первом испытании был вынут черный шар, то вероятность события В увеличивается Р(В) =
,если в первом испытании был вынут черный шар, то вероятность события В увеличивается Р(В) =![]() .
.
Итак, вероятность события В существенно зависит от того, произошло или не произошло событие А, в таких случаях события А и В - зависимые.
Пусть А и В - зависимые события. Условной вероятностью РА(В) события В называют вероятность события В, найденную в предположении, что событие А уже наступило.
Итак, в примере 1 РА(В) =![]() .
.
Заметим, что если события А и В независимы, то РА (В )= Р(В).
Теорема 1. Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие уже наступило:
P(AB)= Р(А)РА(В). (2)
Доказательство.
Пусть из всего числа n элементарных событий k благоприятствуют событию А и пусть из этих k событий l благоприятствуют событию В, а значит, и событию АВ. Тогда Р(АВ)= ![]() =
=![]() .
.![]() = Р(А)РА(В), что и доказывает искомое равенство (2).
= Р(А)РА(В), что и доказывает искомое равенство (2).
Замечание. Применив формулу (2) к событию ВА, получим
Р(ВА) = Р(В)РВ(А). (3)
Так как АВ = ВА, то, сравнивая (2) и (3), получаем, что
Р(А)РА(В) = Р(В)РВ(А).
Пример 2. В условиях примера 1 берем тот случай, когда вынутый шар в первом испытании не кладется обратно в урну. Поставим следующий вопрос: какова вероятность вынуть первый и второй разы белые шары? По формуле (2) имеем
![]()
Теорема 2. Вероятность произведения двух независимых событий А и В равна произведению вероятностей этих событий:
| (4) |
Р(ВА) = Р(А)Р(В).
Действительно, если А и В - независимые события, то РА (В) = = Р(В) и формула (2) превращается в формулу (4).
Пример 3. Вероятность выживания одного организма в течение 20 мин Р = 0,7. В пробирке с благоприятными для существования этих организмов условиями находятся только что родившиеся 2 организма. Какова вероятность того, что через 20 минут они будут живы?
Пусть событие А - первый организм жив через 20 мин, событие В - второй организм жив через 20 мин. Будем считать, что между организмами нет внутривидовой конкуренции, т.е. события А и В независимы. Событие, что оба организма живы, есть событие АВ. По теореме 2 получаем Р(АВ) = 0,7 ∙ 0,7 = 0,49 [7,115].
Теорема сложения вероятностей совместимых событий
Теорема. Вероятность суммы двух совместимых событий А и В равна сумме вероятностей этих событий минус вероятность их произведения
Р(А + В) = Р(А) + Р(В) - Р(АВ). (5)
Доказательство. Пусть из всего числа n элементарных событий k благоприятствуют событию А, l - событию В и m - одновременно событиям А и В. Отсюда событию А + В благоприятствуют к + 1 - m элементарных событий. Тогда
Р(А+В)= ![]() = Р(А) + Р(В) - Р(АВ)
= Р(А) + Р(В) - Р(АВ)
Замечание. Если события А и В несовместимы, то их произведение АВ есть невозможное событие и, следовательно, Р(АВ) = 0, т.е. формула (1) является частным случаем формулы (5).
Пример. В посевах пшеницы на делянке имеется 95% здоровых растений. Выбирают два растения. Определить вероятность того, что среди них хотя бы одно окажется здоровым.
Введем обозначения для событий:
А1- первое растение здоровое;
А2 - второе растение здоровое;
А1+A2 - хотя бы одно растение здоровое.
Так как события А1 и А2 совместимые, то согласно формуле (5)
P(А1+ А2) = P(А1) + P(А2) = 0,95 + 0,95 - 0,95 · 0,95 = 0,9975 ≈ 1 [4, 28].
Формула полной вероятности
Теорема. Вероятность события А, которое может нacmупить лишь при условии появления одного из n попарно несовместимых событий В1, В2, ... Вn , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
![]() (6)
(6)
(формула полной вероятности).
Доказательство. Событие А может наступить лишь при условии наступления одного из событий B1, В2, ..., Bn, т.е. А = B1 А + В2А + ... +, BnА причем ввиду несовместимости событий B1, В2 , ..., BnА события B1А, В2А, ..., BnА также несовместимы. По этому на основании теорем сложения и умножения вероятностей имеем
![]()
Пример 1. Имеются три одинаковых по виду ящика. В первом находят две белые мыши и одна серая, во втором - три белые и одна серая, в третьей две белые и две серые мыши. Какова вероятность того, что из наугад выбранного ящика будет извлечена белая мышь?
Обозначим: B1 - выбор первого ящика, B2 - выбор второго ящика, В3 - выбор третьего ящика, А - извлечение белой мыши. Так как все ящики одинаковы, то P(В1)= Р(В2) = Р(В3) =![]() .
.
Если выбран первый ящик, то![]() (А) =
(А) =![]() . Аналогично
. Аналогично ![]() (А) =
(А) =![]() ,
,![]() (A) =
(A) =![]() . Наконец, по формуле (6) получаем
. Наконец, по формуле (6) получаем ![]() [8, 22].
[8, 22].
Формула Бейеса
Пусть в условиях рассуждения, относящегося к формуле полной вероятности, произведено одно испытание, в результате которого произошло событие А. Спрашивается: как изменились (в связи с тем, что событие А уже произошло) величины P(Bk), k = 1,... , п.
Найдем условную вероятность РA(Вk).
По теореме умножения вероятностей и формуле (3) имеем:
![]()
Отсюда: ![]()
Наконец, используя формулу полной вероятности, находим
 (k=1, 2, …, n). (7)
(k=1, 2, …, n). (7)
Формулу(7) называют формулой Бейеса (Байеса)
Пример. Большая популяция людей разбита на две группы одинаковой численности. Диета одной группы отличалась высоким содержанием ненасыщенных жиров, а диета контрольной группы была богата насыщенными жирами. После 10 лет пребывания на этих диетах возникновение сердечнососудистых заболеваний составило в этих группах соответственно 31% и 48%. Случайно выбранный из популяции человек имеет сердечно-сосудистое заболевание. Какова вероятность того, что этот человек принадлежит к контрольной группе?
![]() Введем обозначения для событий:
Введем обозначения для событий:
А - случайно выбранный из популяции человек имеет сердечно-сосудистое заболевание;
B1 - человек придерживался специальной диеты;
В2 - человек принадлежал к контрольной группе. Имеем
Р(В1) = Р(В2) = 0,5,
![]() (A) = 0,31,
(A) = 0,31, ![]() (A) = 0,48.
(A) = 0,48.
Согласно формуле полной вероятности
Р(А) = 0,5 ∙ 0,31 + 0,5 ∙ 0,48 = 0,395
и, наконец, в силу формулы (7) искомая вероятность
![]() [11, 216].
[11, 216].
Таким образом, можно привести много разнообразных примеров случайных величин. Все же и в мире случайностей обнаруживаются определенные закономерности. Математический аппарат для изучения таких закономерностей и дает теория вероятностей. Она занимается математическим анализом случайных событий и связанных с ними случайных величин.
Для решения задач по теории вероятностей следует применять следующие теоремы: сложения вероятностей несовместимых событий, умножения вероятностей, сложений вероятностей совместимых событий; формулы: полной вероятности, Бейеса (Байеса).
Одной из форм дифференцированного обучения по курсу теории вероятностей может являться факультативный курс.
Похожие работы
... обучения, школа предоставляет учащимся право выбора предметов по интересам и склонностям. В соответствии с требованиями была разработана программа факультативного курса по теме «Элементы комбинаторики» для 8 класса. 2.2 Программа факультативного курса Пояснительная записка В математике и ее приложениях часто приходится иметь дело с различного рода множествами и подмножествами: ...
... способом аналитико – синтетический метод применяется на тех – же решениях. Единственное различие состоит в том , что на этапе поиска решения применяется анализ в нисходящей форме. Методика обучения решения технических задач. Математические задачи, в которых есть хотя бы один объект, являющийся реальным предметом, принято называть текстовыми (сюжетными, практическими, арифметическими и т.д) ...
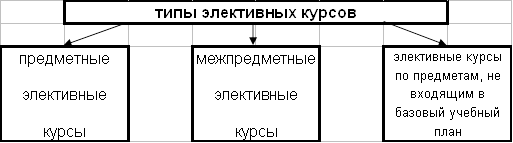
... -иллюстративного и репродуктивного метолов, а экономический профиль ориентирован на формирование прикладного стиля мышления. 2. Методика проведения элективных курсов по математике в профильной школе 2.1 Цели организации элективных курсов по математике Принципиальным положением организации школьного математического образования в настоящее время является дифференциация обучения ...
... при ошибке в его выборе, учитывать по уровневый подход. 4. Математика должна входить в набор обязательных учебных предметов любого из профилей.2 МАТЕМАТИЧЕСКИЙ ФАКУЛЬТАТИВ КАК ВЕДУЩАЯ ФОРМА ПРОФИЛЬНОГО ОБУЧЕНИЯ МАТЕМАТИКЕ В ОБЩЕОБРАЗОВАТЕЛЬНОЙ ШКОЛЕ2.1. Организационно-педагогические условия успешного функционирования математических факультативов Еще на рубеже XIX и XX вв. некоторые ...

0 комментариев