Расчет редуктора

Введение

Инженер-конструктор является творцом новой техники, и уровнем его творческой работы в большей степени определяются темпы научно-технического прогресса. Деятельность конструктора принадлежит к числу наиболее сложных проявлений человеческого разума. Решающая роль успеха при создании новой техники определяется тем, что заложено на чертеже конструктора. С развитием науки и техники проблемные вопросы решаются с учетом все возрастающего числа факторов, базирующихся на данных различных наук. При выполнении проекта используются математические модели, базирующиеся на теоретических и экспериментальных исследованиях, относящихся к объемной и контактной прочности, материаловедению, теплотехнике, гидравлике, теории упругости, строительной механике. Широко используются сведения из курсов сопротивления материалов, теоретической механики, машиностроительного черчения и т.д. Все это способствует развитию самостоятельности и творческого подхода к поставленным проблемам.

При выборе типа редуктора для привода рабочего органа (устройства) необходимо учитывать множество факторов, важнейшими из которых являются: значение и характер изменения нагрузки, требуемая долговечность, надежность, КПД, масса и габаритные размеры, требования к уровню шума, стоимость изделия, эксплуатационные расходы.

Из всех видов передач зубчатые передачи имеют наименьшие габариты, массу, стоимость и потери на трение. Коэффициент потерь одной зубчатой пары при тщательном выполнении и надлежащей смазке не превышает обычно 0,01. Зубчатые передачи в сравнении с другими механическими передачами обладают большой надежностью в работе, постоянством передаточного отношения из-за отсутствия проскальзывания, возможностью применения в широком диапазоне скоростей и передаточных отношений. Эти свойства обеспечили большое распространение зубчатых передач; они применяются для мощностей, начиная от ничтожно малых (в приборах) до измеряемых десятками тысяч киловатт.

К недостаткам зубчатых передач могут быть отнесены требования высокой точности изготовления и шум при работе со значительными скоростями.

Косозубые колеса применяют для ответственных передач при средних и высоких скоростях. Объем их применения – свыше 30% объема применения всех цилиндрических колес в машинах; и этот процент непрерывно возрастает. Косозубые колеса с твердыми поверхностями зубьев требуют повышенной защиты от загрязнений во избежание неравномерного износа по длине контактных линий и опасности выкрашивания.

Одной из целей выполненного проекта является развитие инженерного мышления, в том числе умение использовать предшествующий опыт, моделировать используя аналоги. Для курсового проекта предпочтительны объекты, которые не только хорошо распространены и имеют большое практическое значение, но и не подвержены в обозримом будущем моральному старению.

Существуют различные типы механических передач: цилиндрические и конические, с прямыми зубьями и косозубые, гипоидные, червячные, глобоидные, одно- и многопоточные и т.д. Это рождает вопрос о выборе наиболее рационального варианта передачи. При выборе типа передачи руководствуются показателями, среди которых основными являются КПД, габаритные размеры, масса, плавность работы и вибронагруженность, технологические требования, предпочитаемое количество изделий.

При выборе типов передач, вида зацепления, механических характеристик материалов необходимо учитывать, что затраты на материалы составляют значительную часть стоимости изделия: в редукторах общего назначения – 85%, в дорожных машинах – 75%, в автомобилях – 10% и т.д.

Поиск путей снижения массы проектируемых объектов является важнейшей предпосылкой дальнейшего прогресса, необходимым условием сбережения природных ресурсов. Большая часть вырабатываемой в настоящее время энергии приходится на механические передачи, поэтому их КПД в известной степени определяет эксплуатационные расходы.

Наиболее полно требования снижения массы и габаритных размеров удовлетворяет привод с использованием электродвигателя и редуктора с внешним зацеплением.

1. Выбор электродвигателя и кинематический расчёт

По табл. 1.1 [1] примем следующие значения КПД:

– для закрытой зубчатой цилиндрической передачи: h1 = 0,975

– для закрытой зубчатой цилиндрической передачи: h2 = 0,975

Общий КПД привода будет:

h = h1 · … · hn · hподш. 3 · hмуфты2 = 0,975 · 0,975 · 0,993 · 0,982 = 0,886

где hподш. = 0,99 – КПД одного подшипника.

hмуфты = 0,98 – КПД одной муфты.

Угловая скорость на выходном валу будет:

wвых. = 2 · V / D = 2 · 3 · 103 / 320 = 18,75 рад/с

Требуемая мощность двигателя будет:

Pтреб. = F · V / h = 3,5 · 3 / 0,886 = 11,851 кВт

В таблице П. 1 [1] (см. приложение) по требуемой мощности выбираем электродвигатель 160S4, с синхронной частотой вращения 1500 об/мин, с параметрами: Pдвиг.=15 кВт и скольжением 2,3% (ГОСТ 19523–81). Номинальная частота вращения nдвиг. = 1500–1500·2,3/100=1465,5 об/мин, угловая скорость wдвиг. = p · nдвиг. / 30 = 3,14 · 1465,5 / 30 = 153,467 рад/с.

Oбщее передаточное отношение:

u = wвход. / wвых. = 153,467 / 18,75 = 8,185

Для передач выбрали следующие передаточные числа:

u1 = 3,15

u2 = 2,5

Рассчитанные частоты и угловые скорости вращения валов сведены ниже в таблицу:

Вал 1-й	n1 = nдвиг. = 1465,5 об./мин.	w1 = wдвиг. = 153,467 рад/c.
Вал 2-й	n2 = n1 / u1 = 1465,5 / 3,15 = 465,238 об./мин.	w2 = w1 / u1 = 153,467 / 3,15 = 48,72 рад/c.
Вал 3-й	n3 = n2 / u2 = 465,238 / 2,5 = 186,095 об./мин.	w3 = w2 / u2 = 48,72 / 2,5 = 19,488 рад/c.

Мощности на валах:

P1 = Pтреб. · hподш. · h(муфты 1) = 11,851 · 103 · 0,99 · 0,98 = 11497,84 Вт

P2 = P1 · h1 · hподш. = 11497,84 · 0,975 · 0,99 = 11098,29 Вт

P3 = P2 · h2 · hподш. = 11098,29 · 0,975 · 0,99 = 10393,388 Вт

Вращающие моменты на валах:

T1 = P1 / w1 = (11497,84 · 103) / 153,467 = 74920,602 Н·мм

T2 = P2 / w2 = (11098,29 · 103) / 48,72 = 227797,414 Н·мм

T3 = P3 / w3 = (10393,388 · 103) / 19,488 = 533322,455 Н·мм

По таблице П. 1 (см. приложение учебника Чернавского) выбран электродвигатель 160S4, с синхронной частотой вращения 1500 об/мин, с мощностью Pдвиг.=15 кВт и скольжением 2,3% (ГОСТ 19523–81). Номинальная частота вращения с учётом скольжения nдвиг. = 1465,5 об/мин.

Передаточные числа и КПД передач

Передачи	Передаточное число	КПД
1-я закрытая зубчатая цилиндрическая передача	3,15	0,975
2-я закрытая зубчатая цилиндрическая передача	2,5	0,975

Рассчитанные частоты, угловые скорости вращения валов и моменты на валах

Валы	Частота вращения, об/мин	Угловая скорость, рад/мин	Момент, Нxмм
1-й вал	1465,5	153,467	74920,602
2-й вал	465,238	48,72	227797,414
3-й вал	186,095	19,488	533322,455

2. Расчёт 1-й зубчатой цилиндрической передачи

2.1 Проектный расчёт

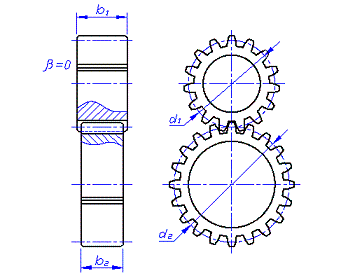
Так как в задании нет особых требований в отношении габаритов передачи, выбираем материалы со средними механическими характеристиками (см. гл. 3, табл. 3.3 [1]):

– для шестерни: сталь: 45

термическая обработка: улучшение

твердость: HB 230

– для колеса: сталь: 45

термическая обработка: улучшение

твердость: HB 200

Допустимые контактные напряжения (формула (3.9) [1]), будут:

[sH] = sH lim b · KHL / [SH]

По таблице 3.2 гл. 3 [1] имеем для сталей с твердостью поверхностей зубьев менее HB 350:

sH lim b = 2 · HB + 70.

sH lim b (шестерня) = 2 · 230 + 70 = 530 МПа;

sH lim b (колесо) = 2 · 200 + 70 = 470 МПа;

[SH] – коэффициент безопасности [SH]=1,1; KHL – коэффициент долговечности.

KHL = (NH0 / NH) 1/6,

где NH0 – базовое число циклов нагружения; для стали шестерни NH0 (шест.) = 17000000; для стали колеса NH0 (кол.) = 10000000;

NH = 60 · n · c · tS

Здесь:

– n – частота вращения, об./мин.; nшест. = 1465,502 об./мин.; nкол. = 465,239 об./мин.

– c = 1 – число колёс, находящихся в зацеплении;

tS = 20000 ч. – продолжительность работы передачи в расчётный срок службы.

Тогда:

NH (шест.) = 60 · 1465,502 · 1 · 20000 = 1758602400

NH (кол.) = 60 · 465,239 · 1 · 20000 = 558286800

В итоге получаем:

КHL (шест.) = (17000000 / 1758602400) 1/6 = 0,462

Так как КHL (шест.)<1.0, то принимаем КHL (шест.) = 1

КHL (кол.) = (10000000 / 558286800) 1/6 = 0,512

Так как КHL (кол.)<1.0, то принимаем КHL (кол.) = 1

Допустимые контактные напряжения:

для шестерни [sH1] = 530 · 1 / 1,1 = 481,818 МПа;

для колеса [sH2] = 470 · 1 / 1,1 = 427,273 МПа.

Для прямозубых колес за расчетное напряжение принимается минимальное допустимое контактное напряжение шестерни или колеса.

Тогда расчетное допускаемое контактное напряжение будет:

[sH] = [sH2] = 427,273 МПа.

Принимаем коэффициент симметричности расположения колес относительно опор по таблице 3.5 [1]: KHb = 1,25.

Коэффициент ширины венца по межосевому расстоянию принимаем: yba = b / aw = 0,2, (см. стр. 36 [1]).

Межосевое расстояние из условия контактной выносливости активных поверхностей зубьев найдем по формуле 3.7 гл. 3 [1]:

aw = Ka · (u + 1) · (T2 · KHb / [sH] 2 · u2 · yba) 1/3 =

49.5 · (3,15 + 1) · (227797,414 · 1,25 / 427,2732 · 3,152 · 0,2) 1/3 = 189,577 мм.

где для прямозубых колес Кa = 49.5, передаточное число передачи u = 3,15; T2 = Тколеса = 227797,414 Н·мм – момент на колесе.

Ближайшее значение межосевого расстояния по ГОСТ 2185–66 будет: aw = 180 мм.

Нормальный модуль зацепления берем по следующей рекомендации:

mn = (0.01…0.02) · aw мм, для нас: mn = 1,8.. 3,6 мм, принимаем:

по ГОСТ 9563–60* (см. стр. 36 [1]) mn = 2 мм.

Задаемся суммой зубьев:

SZ = z1 + z2 = 2 · aw / mn = 2 · 180 / 2 = 180

Числа зубьев шестерни и колеса:

z1 = SZ / (u + 1) = 180 / (3,15 + 1) = 43,373

Принимаем: z1 = 43

z2 = SZ – z1 = 180 – 43 = 137

Угол наклона зубьев b = 0o.

Основные размеры шестерни и колеса:

диаметры делительные:

d1 = mn · z1 / cos(b) = 2 · 43 / cos(0o) = 86 мм;

d2 = mn · z2 / cos(b) = 2 · 137 / cos(0o) = 274 мм.

Проверка: aw = (d1 + d2) / 2 = (86 + 274) / 2 = 180 мм.

диаметры вершин зубьев:

da1 = d1 + 2 · mn = 86 + 2 · 2 = 90 мм;

da2 = d2 + 2 · mn = 274 + 2 · 2 = 278 мм.

ширина колеса: b2 = yba · aw = 0,2 · 180 = 36 мм;

ширина шестерни: b1 = b2 + 5 = 36 + 5 = 41 мм;

Определим коэффициент ширины шестерни по диаметру:

ybd = b1 / d1 = 41 / 86 = 0,477

Окружная скорость колес будет:

V = w1 · d1 / 2 = 153,467 · 86 · 10–3 / 2 = 6,599 м/c;

При такой скорости следует принять для зубчатых колес 7-ю степень точности.

Коэффициент нагрузки равен:

KH = KHb · KHa · KHv.

Коэффициент KHb=1,048 выбираем по таблице 3.5 [1], коэффициент KHa=1 выбираем по таблице 3.4 [1], коэффициент KHv=1,07 выбираем по таблице 3.6 [1], тогда:

KH = 1,048 · 1 · 1,07 = 1,121

2.2 Проверочный расчёт по контактным напряжениям

Проверку контактных напряжений проводим по формуле 3.6 [1]:

sH = (310 / aw) · ((T2 · KH · (u + 1) 3) / (b2 · u2)) 1/2 =

(310 / 180) · ((227797,414 · 1,121 · (3,15 + 1) 3; 36 · 3,152))

= 389,293 МПа. £ [sH]

Силы, действующие в зацеплении вычислим по формуле 8.3 и 8.4 [1]:

окружная: Ft = 2 · T1 / d1 = 2 · 74920,602 / 86 = 1742,34 Н;

радиальная: Fr = Ft · tg(a) / cos(b) = 1742,34 · tg(20o) / cos(0o) = 634,16 Н;

осевая: Fa = F t · tg(b) = 1742,34 · tg(0o) = 0 Н.

2.3 Проверка зубьев передачи на изгиб

Проверим зубья на выносливость по напряжениям изгиба по формуле 3.22 [1]:

sF = Ft · KF · YF / (b · mn) £ [sF]

Здесь коэффициент нагрузки KF = KFb · KFv (см. стр. 42 [1]). По таблице 3.7 [1] выбираем коэффициент расположения колес KFb = 1,089, по таблице 3.8 [1] выбираем коэффициент KFv=1,35. Таким образом коэффициент KF = 1,089 · 1,35 = 1,47. Y – коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа Zv (см. гл. 3, пояснения к формуле 3.25 [1]):

у шестерни: Zv1 = z1 / cos3 (b) = 43 / cos3 (0o) = 43

у колеса: Zv2 = z2 / cos3 (b) = 137 / cos3 (0o) = 137

Тогда: YF1 = 3,688; YF2 = 3,582

Допускаемые напряжения находим по формуле 3.24 [1]:

[sF] = soF lim b · KFL / [Sf].

KFL – коэффициент долговечности.

KFL = (NFO / NF) 1/6,

где NFO – базовое число циклов нагружения; для данных сталей NFO = 4000000;

NF = 60 · n · c · tS

Здесь:

– n – частота вращения, об./мин.; nшест. = 1465,502 об./мин.; nкол. = 465,239 об./мин.

– c = 1 – число колёс, находящихся в зацеплении;

tS = 20000 ч. – продолжительность работы передачи в расчётный срок службы.

Тогда:

NF (шест.) = 60 · 1465,502 · 1 · 20000 = 1758602400

NF (кол.) = 60 · 465,239 · 1 · 20000 = 558286800

В итоге получаем:

КFL (шест.) = (4000000 / 1758602400) 1/6 = 0,363

Так как КFL (шест.)<1.0, то принимаем КFL (шест.) = 1

КFL (кол.) = (4000000 / 558286800) 1/6 = 0,439

Так как КFL (шест.)<1.0, то принимаем КFL (шест.) = 1

Для шестерни: soF lim b = 414 МПа;

Для колеса: soF lim b = 360 МПа.

Коэффициент [SF] безопасности находим по формуле 3.24 [1]:

[SF] = [SF]' · [SF]».

где для шестерни [SF]' = 1,75;

[SF]' = 1;

[SF (шест.)] = 1,75 · 1 = 1,75

для колеса [SF]' = 1,75;

[SF]» = 1.

[SF (кол.)] = 1,75 · 1 = 1,75

Допускаемые напряжения:

для шестерни: [sF1] = 414 · 1 / 1,75 = 236,571 МПа;

для колеса: [sF2] = 360 · 1 / 1,75 = 205,714 МПа;

Находим отношения [sF] / YF:

для шестерни: [sF1] / YF1 = 236,571 / 3,688 = 64,146

для колеса: [sF2] / YF2 = 205,714 / 3,582 = 57,43

Дальнейший расчет будем вести для колеса, для которого найденное отношение меньше.

Проверяем прочность зуба колеса по формуле 3.25 [1]:

sF2 = (Ft · KF · YF1) / (b2 · mn) =

(1742,34 · 1,47 · · 3,582) / (36 · 2) = 127,422 МПа

sF2 = 127,422 МПа < [sf] = 205,714 МПа.

Условие прочности выполнено.

Механические характеристики материалов зубчатой передачи

Элемент передачи	Марка стали	Термообработка	HB1ср	sв	[s] H	[s] F
			HB2ср	H/мм2
Шестерня	45	улучшение	230	780	481,818	236,571
Колесо	45	улучшение	200	690	427,273	205,714

Параметры зубчатой цилиндрической передачи, мм

Проектный расчёт
Параметр		Значение		Параметр			Значение
Межосевое расстояние aw		180		Угол наклона зубьев b, град			0
Модуль зацепления m		2		Диаметр делительной окружности:
Ширина зубчатого венца:				шестерни d1 колеса d2			86 274
шестерни b1 колеса b2		41 36
Числа зубьев:				Диаметр окружности вершин:
шестерни z1 колеса z2		43 137		шестерни da1 колеса da2			90 278
Вид зубьев		прямозубая передача		Диаметр окружности впадин:
				шестерни df1 колеса df2			81 269
Проверочный расчёт
Параметр			Допускаемые значения		Расчётные значения	Примечание
Контактные напряжения sH, H/мм2			427,273		389,293	-
Напряжения изгиба, H/мм2	sF1		236,571		115,193	-
	sF2		205,714		127,422	-

3. Расчёт 2-й зубчатой цилиндрической передачи

3.1 Проектный расчёт

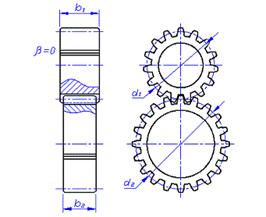
Так как в задании нет особых требований в отношении габаритов передачи, выбираем материалы со средними механическими характеристиками (см. гл. 3, табл. 3.3 [1]):

– для шестерни: сталь: 40ХН

термическая обработка: улучшение

твердость: HB 280

– для колеса: сталь: 40ХН

термическая обработка: улучшение

твердость: HB 265

Допустимые контактные напряжения (формула (3.9) [1]), будут:

[sH] = sH lim b · KHL / [SH]

По таблице 3.2 гл. 3 [1] имеем для сталей с твердостью поверхностей зубьев менее HB 350:

sH lim b = 2 · HB + 70.

sH lim b (шестерня) = 2 · 280 + 70 = 630 МПа;

sH lim b (колесо) = 2 · 265 + 70 = 600 МПа;

[SH] – коэффициент безопасности [SH]=1,1; KHL – коэффициент долговечности.

KHL = (NH0 / NH) 1/6,

где NH0 – базовое число циклов нагружения; для данных сталей NH0 = 26400000;

NH = 60 · n · c · tS

Здесь:

– n – частота вращения, об./мин.; nшест. = 465,242 об./мин.; nкол. = 186,097 об./мин.

– c = 1 – число колёс, находящихся в зацеплении;

tS = 20000 ч. – продолжительность работы передачи в расчётный срок службы.

Тогда:

NH (шест.) = 60 · 465,242 · 1 · 20000 = 558290400

NH (кол.) = 60 · 186,097 · 1 · 20000 = 223316400

В итоге получаем:

КHL (шест.) = (26400000 / 558290400) 1/6 = 0,601

Так как КHL (шест.)<1.0, то принимаем КHL (шест.) = 1

КHL (кол.) = (26400000 / 223316400) 1/6 = 0,701

Так как КHL (кол.)<1.0, то принимаем КHL (кол.) = 1

Допустимые контактные напряжения:

для шестерни [sH1] = 630 · 1 / 1,1 = 572,727 МПа;

для колеса [sH2] = 600 · 1 / 1,1 = 545,455 МПа.

Для прямозубых колес за расчетное напряжение принимается минимальное допустимое контактное напряжение шестерни или колеса.

Тогда расчетное допускаемое контактное напряжение будет:

[sH] = [sH2] = 545,455 МПа.

Принимаем коэффициент симметричности расположения колес относительно опор по таблице 3.5 [1]: KHb = 1,25.

Коэффициент ширины венца по межосевому расстоянию принимаем: yba = b / aw = 0,25, (см. стр. 36 [1]).

Межосевое расстояние из условия контактной выносливости активных поверхностей зубьев найдем по формуле 3.7 гл. 3 [1]:

aw = Ka · (u + 1) · (T2 · KHb / [sH] 2 · u2 · yba) 1/3 =

49.5 · (2,5 + 1) · (533322,455 · 1,25 / 545,4552 · 2,52 · 0,25) 1/3 = 195,371 мм.

где для прямозубых колес Кa = 49.5, передаточное число передачи u = 2,5; T2 = Тколеса = 533322,455 Н·мм – момент на колесе.

Ближайшее значение межосевого расстояния по ГОСТ 2185–66 будет: aw = 180 мм.

Нормальный модуль зацепления берем по следующей рекомендации:

mn = (0.01…0.02) · aw мм, для нас: mn = 1,8.. 3,6 мм, принимаем:

по ГОСТ 9563–60* (см. стр. 36 [1]) mn = 2 мм.

Задаемся суммой зубьев:

SZ = z1 + z2 = 2 · aw / mn = 2 · 180 / 2 = 180

Числа зубьев шестерни и колеса:

z1 = SZ / (u + 1) = 180 / (2,5 + 1) = 51,429

Принимаем: z1 = 51

z2 = SZ – z1 = 180 – 51 = 129

Угол наклона зубьев b = 0o.

Основные размеры шестерни и колеса:

диаметры делительные:

d1 = mn · z1 / cos(b) = 2 · 51 / cos(0o) = 102 мм;

d2 = mn · z2 / cos(b) = 2 · 129 / cos(0o) = 258 мм.

Проверка: aw = (d1 + d2) / 2 = (102 + 258) / 2 = 180 мм.

диаметры вершин зубьев:

da1 = d1 + 2 · mn = 102 + 2 · 2 = 106 мм;

da2 = d2 + 2 · mn = 258 + 2 · 2 = 262 мм.

ширина колеса: b2 = yba · aw = 0,25 · 180 = 45 мм;

ширина шестерни: b1 = b2 + 5 = 45 + 5 = 50 мм;

Определим коэффициент ширины шестерни по диаметру:

ybd = b1 / d1 = 50 / 102 = 0,49

Окружная скорость колес будет:

V = w1 · d1 / 2 = 48,72 · 102 · 10–3 / 2 = 2,485 м/c;

При такой скорости следует принять для зубчатых колес 8-ю степень точности.

Коэффициент нагрузки равен:

KH = KHb · KHa · KHv.

Коэффициент KHb=1,049 выбираем по таблице 3.5 [1], коэффициент KHa=1 выбираем по таблице 3.4 [1], коэффициент KHv=1,05 выбираем по таблице 3.6 [1], тогда:

KH = 1,049 · 1 · 1,05 = 1,101

3.2 Проверочный расчёт по контактным напряжениям

Проверку контактных напряжений проводим по формуле 3.6 [1]:

sH = (310 / aw) · ((T2 · KH · (u + 1) 3) / (b2 · u2)) 1/2 =

(310 / 180) · ((533322,455 · 1,101 · (2,5 + 1) 3; 45 · 2,52)) =

515,268 МПа. £ [sH]

Силы действующие в зацеплении вычислим по формуле 8.3 и 8.4 [1]:

окружная: Ft = 2 · T1 / d1 = 2 · 227797,414 / 102 = 4466,616 Н;

радиальная: Fr = Ft · tg(a) / cos(b) = 4466,616 · tg(20o) / cos(0o) = 1625,715 Н;

осевая: Fa = F t · tg(b) = 4466,616 · tg(0o) = 0 Н.

3.3 Проверка зубьев передачи на изгиб

Проверим зубья на выносливость по напряжениям изгиба по формуле 3.22 [1]:

sF = Ft · KF · YF / (b · mn) £ [sF]

Здесь коэффициент нагрузки KF = KFb · KFv (см. стр. 42 [1]). По таблице 3.7 [1] выбираем коэффициент расположения колес KFb = 1,092, по таблице 3.8 [1] выбираем коэффициент KFv=1,25. Таким образом коэффициент KF = 1,092 · 1,25 = 1,365. Y – коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа Zv (см. гл. 3, пояснения к формуле 3.25 [1]):

у шестерни: Zv1 = z1 / cos3 (b) = 51 / cos3 (0o) = 51

у колеса: Zv2 = z2 / cos3 (b) = 129 / cos3 (0o) = 129

Тогда: YF1 = 3,656; YF2 = 3,586

Допускаемые напряжения находим по формуле 3.24 [1]:

[sF] = soF lim b · KFL / [Sf].

KFL – коэффициент долговечности.

KFL = (NFO / NF) 1/6,

где NFO – базовое число циклов нагружения; для данных сталей NFO = 4000000;

NF = 60 · n · c · tS

Здесь:

– n – частота вращения, об./мин.; nшест. = 465,242 об./мин.; nкол. = 186,097 об./мин.

– c = 1 – число колёс, находящихся в зацеплении;

tS = 20000 ч. – продолжительность работы передачи в расчётный срок службы.

Тогда:

NF (шест.) = 60 · 465,242 · 1 · 20000 = 558290400

NF (кол.) = 60 · 186,097 · 1 · 20000 = 223316400

В итоге получаем:

КFL (шест.) = (4000000 / 558290400) 1/6 = 0,439

Так как КFL (шест.)<1.0, то принимаем КFL (шест.) = 1

КFL (кол.) = (4000000 / 223316400) 1/6 = 0,512

Так как КFL (шест.)<1.0, то принимаем КFL (шест.) = 1

Для шестерни: soF lim b = 504 МПа;

Для колеса: soF lim b = 477 МПа.

Коэффициент [SF] безопасности находим по формуле 3.24 [1]:

[SF] = [SF]' · [SF]».

где для шестерни [SF]' = 1,75;

[SF]' = 1;

[SF (шест.)] = 1,75 · 1 = 1,75

для колеса [SF]' = 1,75;

[SF]» = 1.

[SF (кол.)] = 1,75 · 1 = 1,75

Допускаемые напряжения:

для шестерни: [sF1] = 504 · 1 / 1,75 = 288 МПа;

для колеса: [sF2] = 477 · 1 / 1,75 = 272,571 МПа;

Находим отношения [sF] / YF:

для шестерни: [sF1] / YF1 = 288 / 3,656 = 78,775

для колеса: [sF2] / YF2 = 272,571 / 3,586 = 76,01

Дальнейший расчет будем вести для колеса, для которого найденное отношение меньше.

Проверяем прочность зуба колеса по формуле 3.25 [1]:

sF2 = (Ft · KF · YF1) / (b2 · mn) =

(4466,616 · 1,365 · · 3,586) / (45 · 2) = 242,929 МПа

sF2 = 242,929 МПа < [sf] = 272,571 МПа.

Условие прочности выполнено.

Механические характеристики материалов зубчатой передачи

Элемент передачи	Марка стали	Термообработка	HB1ср	sв	[s] H	[s] F
			HB2ср	H/мм2
Шестерня	40ХН	улучшение	280	930	572,727	288
Колесо	40ХН	улучшение	265	880	545,455	272,571

Параметры зубчатой цилиндрической передачи, мм

Проектный расчёт
Параметр			Значение		Параметр		Значение
Межосевое расстояние aw			180		Угол наклона зубьев b, град		0
Модуль зацепления m			2		Диаметр делительной окружности:
Ширина зубчатого венца:					шестерни d1 колеса d2		102 258
шестерни b1 колеса b2			50 45
Числа зубьев:					Диаметр окружности вершин:
шестерни z1 колеса z2			51 129		шестерни da1 колеса da2		106 262
Вид зубьев			прямозубая передача		Диаметр окружности впадин:
					шестерни df1 колеса df2		97 253
Проверочный расчёт
Параметр		Допускаемые значения		Расчётные значения		Примечание
Контактные напряжения sH, H/мм2		545,455		515,268		-
Напряжения изгиба, H/мм2	sF1	288		222,904		-
	sF2	272,571		242,929		-

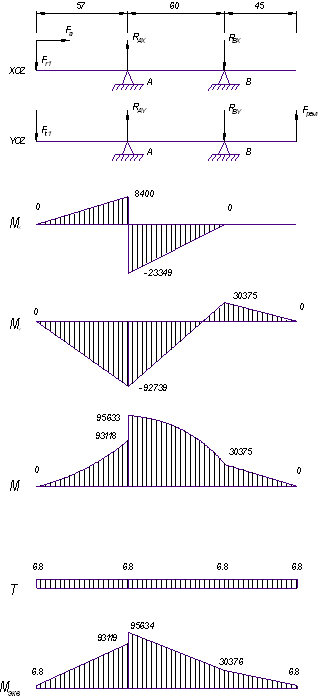
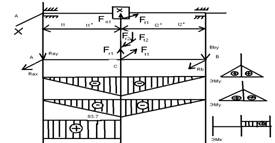
4. Предварительный расчёт валов

Предварительный расчёт валов проведём на кручение по пониженным допускаемым напряжениям.

Диаметр вала при допускаемом напряжении [tк] = 20 МПа вычисляем по формуле 8.16 [1]:

dв ³ (16 · Tк / (p · [tк])) 1/3

4.1 Ведущий вал

dв ³ (16 · 74920,602 / (3,142 · 20)) 1/3 = 26,721 мм.

Под 1-й элемент (подшипник) выбираем диаметр вала: 40 мм.

Под 2-й элемент (ведущий) выбираем диаметр вала: 45 мм.

Под 3-й элемент (подшипник) выбираем диаметр вала: 40 мм.

Под свободный (присоединительный) конец вала выбираем диаметр вала: 36 мм.

4.2 2-й вал

dв ³ (16 · 227797,414 / (3,142 · 20)) 1/3 = 38,711 мм.

Под 1-й элемент (подшипник) выбираем диаметр вала: 45 мм.

Под 2-й элемент (ведущий) выбираем диаметр вала: 50 мм.

Под 3-й элемент (ведомый) выбираем диаметр вала: 55 мм.

Под 4-й элемент (подшипник) выбираем диаметр вала: 45 мм.

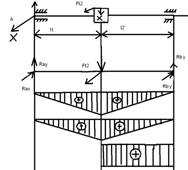
4.3 Выходной вал

dв ³ (16 · 533322,455 / (3,142 · 20)) 1/3 = 51,402 мм.

Под свободный (присоединительный) конец вала выбираем диаметр вала: 55 мм.

Под 2-й элемент (подшипник) выбираем диаметр вала: 60 мм.

Под 3-й элемент (ведомый) выбираем диаметр вала: 65 мм.

Под 4-й элемент (подшипник) выбираем диаметр вала: 60 мм.

Диаметры участков валов назначаем исходя из конструктивных соображений.

Диаметры валов, мм

Валы	Расчетный диаметр	Диаметры валов по сечениям
		1-е сечение	2-е сечение	3-е сечение	4-е сечение
Ведущий вал.	26,721	Под 1-м элементом (подшипником) диаметр вала: 40	Под 2-м элементом (ведущим) диаметр вала: 45	Под 3-м элементом (подшипником) диаметр вала: 40	Под свободным (присоединительным) концом вала: 36
2-й вал.	38,711	Под 1-м элементом (подшипником) диаметр вала: 45	Под 2-м элементом (ведущим) диаметр вала: 50	Под 3-м элементом (ведомым) диаметр вала: 55	Под 4-м элементом (подшипником) диаметр вала: 45
Выходной вал.	51,402	Под свободным (присоединительным) концом вала: 55	Под 2-м элементом (подшипником) диаметр вала: 60	Под 3-м элементом (ведомым) диаметр вала: 65	Под 4-м элементом (подшипником) диаметр вала: 60

Длины участков валов, мм

Валы	Длины участков валов между
	1-м и 2-м сечениями	2-м и 3-м сечениями	3-м и 4-м сечениями
Ведущий вал.	130	65	120
2-й вал.	75	55	65
Выходной вал.	130	75	120

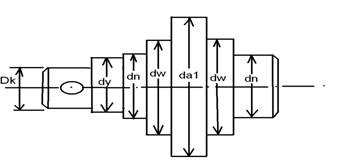
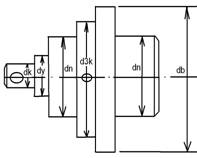
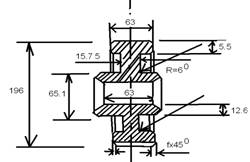
5. Конструктивные размеры шестерен и колёс   5.1 Цилиндрическая шестерня 1-й передачи

Диаметр ступицы: dступ = (1,5…1,8) · dвала = 1,5 · 45 = 67,5 мм. = 68 мм.

Длина ступицы: Lступ = (0,8…1,5) · dвала = 0,8 · 45 = 36 мм = 41 мм.

Фаска: n = 0,5 · mn = 0,5 · 2 = 1 мм

5.2 Цилиндрическое колесо 1-й передачи

Диаметр ступицы: dступ = (1,5…1,8) · dвала = 1,5 · 55 = 82,5 мм. = 82 мм.

Длина ступицы: Lступ = (0,8…1,5) · dвала = 0,8 · 55 = 44 мм

Толщина обода: dо = (2,5…4) · mn = 2,5 · 2 = 5 мм.

Так как толщина обода должна быть не менее 8 мм, то принимаем dо = 8 мм.

где mn = 2 мм – модуль нормальный.

Толщина диска: С = (0,2…0,3) · b2 = 0,2 · 36 = 7,2 мм = 7 мм.

где b2 = 36 мм – ширина зубчатого венца.

Толщина рёбер: s = 0,8 · C = 0,8 · 7 = 5,6 мм = 6 мм.

Внутренний диаметр обода:

Dобода = Da2 – 2 · (2 · mn + do) = 278 – 2 · (2 · 2 + 8) = 254 мм

Диаметр центровой окружности:

DC отв. = 0,5 · (Doбода + dступ.) = 0,5 · (254 + 82) = 168 мм = 169 мм

где Doбода = 254 мм – внутренний диаметр обода.

Диаметр отверстий: Dотв. = Doбода – dступ.) / 4 = (254 – 82) / 4 = 43 мм

Фаска: n = 0,5 · mn = 0,5 · 2 = 1 мм