Побудова логарифмічної моделі

4. Побудова логарифмічної моделі

 

Логарифмічно лінійна модель системи з трьох змінних запишеться у вигляді:

λ_ijk^ABC (4.1)

де ln(n_ijk) – очікувана частота чарунка (і, j, k) тривимірної таблиці спряженості, обчислена за умови незалежності змінних A, B, C; параметри λ визначають внесок у логарифм очікуваної частоти змінних як окремо , так і внаслідок їхньої взаємодії. Параметри λ логлінійної моделі задовольняють умовам:

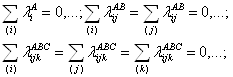 (4.2)

Оцінки параметрів обчислюються за методом максимальної правдоподібності:

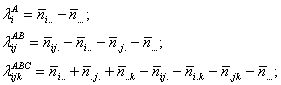 (4.3)

Точка в індексі означає середнє значення за цим індексом, так:

 (4.4)

де n_ijk - частота комірки (і, j, k), яка спостерігається N – число комірок таблиці спряженості.

Оцінка дисперсії параметра λ для насиченої моделі дорівнює

 (4.5)

де δ_ii^ZA = 1, якщо А належить групі змінних Z и , в супротивному разі δ_ii^ZA = 0. Аналогічно обчислюються δ_jj^ZB, δ_kk^ZC.

Якщо поділити, знайдену в результаті розрахунків оцінку на оцінку його середнє квадратичного відхилення , то одержимо стандартизоване значення оцінки параметра. Це значення може бути використане для порівняння відносного внеску кожного параметра в n_ijk, тим самим для обчислення порівняльного значення впливу окремих змінних, кожному парний і множинному взаємозв'язки.

Відзначається, що, крім з насиченої моделі стандартизовані параметри , рівні нулю, можна перейти до моделі, більш адекватної вихідних даних або апріорним припущенням про відносини між змінними.

Одержуємо модель ієрархічну за побудовою, оскільки модель врахована множинна взаємодія A, B, C, а це означає припущення існування зв'язків у будь-якій підгрупі зі складових "старших" взаємозв'язок (ABC) змінних, і тому в модель включені такі параметри, як λ^AB, λ^BC, λ^AC, λ^A, λ^B, λ^C. Якщо ж передбачається, що між змінними немає взаємозв'язків, то у модель не включається відповідний параметр λ . Порядок логлинейной моделі дорівнює найбільшому числу змінних.

Побудова моделі складається з наступних основних етапів: 1) означення порядку логлінійної моделі; 2) відбір параметрів заданого порядку для включення в підсумкову модель.

Логлінійна модель має порядок к, якщо будь-які до к + 1 і більше змінних одночасно незалежні. Тому для означення порядку моделі перевіряються гіпотези про незалежність будь-яких до к + 1 і більш змінних за допомогою критеріїв и  (максимальної правдоподібності). Число ступенів вільності для обох статистик дорівнює n-p, де n – число всіх комірок таблиці, а p – число оцінюваних очікуваних частот за умови незалежності змінних.

Крім того, для кожного к-го порядку перевіряється гіпотеза про одночасну незалежність відповідних ним змінних за допомогою цих же критеріїв.

Так, для параметрів третього порядку перевіряється гіпотеза про відсутність потрійної взаємодії.

Спільна перевірка викладених вище гіпотез дозволяє визначити порядок моделі, що щонайкраще відбиває структуру взаємозв'язків змінних.

Наступним етапом є відбір параметрів моделі, тобто включення в модель тільки тих параметрів, які відбивають істотні впливи й взаємодії змінних. Для розв’язання цієї задачі (перевірки відповідної гіпотези) використовується критерій .

Спочатку обчислюється різниця значень критеріїв , розрахованих відповідно для насиченої моделі к-го порядку й моделі, що відрізняється від насиченої моделі параметром, який перевіряється на значущість. Критерій, побудований у такий спосіб називається критерієм приватного зв'язку змінних. Критерій  для маргінального зв'язку будуватися подібним чином лише з тією різницею, що його значення обчислюються за таблицею, знайденою підсумовуванням частот вихідної багатомірної таблиці спряженості за критеріями змін, що не входять у досліджуваний на значущість параметр. Число ступенів вільності для критеріїв частинного й маргінального зв'язку для групи змінних Z обчислюється за формулою :

 (4.6)

де I, J, K – число рівнів ознак A, B, C відповідно, δ^ZA = 1, якщо А входить в Z, і а якщо ні, то δ^ZA = 0 і т. п.

Критерії частинного і маргінального зв'язків еквівалентні за λ параметрами, які представляють вплив окремо взятих змінних. Відбір параметрів проводитися за наступним правилом: а) якщо обидва критерії (частинного і маргінального зв'язку) показують значущість параметра, то він не виключається з початкової повної моделі; б) якщо обидва критерії вказують на його незначущість, то параметр виключається з моделі; в) якщо ж за одним з критеріїв параметр значущий, а за іншим - ні, то необхідно проводити спеціальне дослідження.

Висновки

Логлінійний аналіз – це статистичний аналіз зв’язку таблиць спряженості за допомогою логлінійних моделей. Логлінійна модель для трьох змінних має вигляд:

де f_ijk,λ – невідомі параметри, які називаються:

λ_i^A– ефект i-ого рівня ознаки А, i=1,..,I;

λ_j^B- ефект j -ого рівня ознаки B, j=1,..,J;

λ_k^C- ефект k-ого рівня ознаки C, k=1,..,K;

λ_ij^AB– ефект взаємодії i-ого рівня ознаки А та j -ого рівня ознаки B;

λ_ik^AC– ефект взаємодії i-ого рівня ознаки А та k-ого рівня ознаки C;

λ_jk^BC- ефект взаємодії j -ого рівня ознаки B та k-ого рівня ознаки C;

λ_ijk^ABC – ефект взаємодії i-ого рівня ознаки А, j -ого рівня ознаки B та k-ого рівня ознаки C;

f_ijk- гіпотетична частота в (i,j,k)-ій комірці

Оцінки параметрів знаходяться за методом максимальної правдоподібності й набувають вигляду:

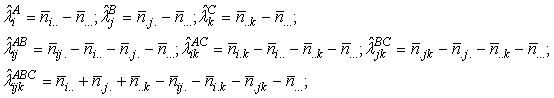
де

Для перевірки гіпотез

H₀: λ_ij^AB=0, i=1,..,I, j=1,..,J – про незалежність ознак А і В;

H₀: λ_ik^AC=0, i=1,..,I, k=1,..,K – гіпотеза про незалежність ознак А і C;

H₀: λ_jk^BC=0, j=1,..,J, k=1,..,K – гіпотеза про незалежність ознак B і C;

H₀: λ_ijk^ABC=0, i=1,..,I, j=1,..,J, k=1,..,K – гіпотеза про незалежність ознак A, B і C

використовують критерій та критерій частинного зв’язку ознак.

Критерій . Якщо гіпотезу Н₀ відхиляти при:

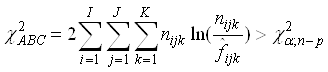
і не відхиляти в супротивному разі, то з імовірністю α гіпотеза відхиляється, коли вона справедлива. n – кількість всіх комірок, p - число оцінюваних очікуваних частот при умові незалежності змінних,

Критерій частинного зв’язку ознак. Якщо гіпотезу Н₀ про взаємозв’язок ознак А і В відхиляти при

і не відхиляти в супротивному разі, то з імовірністю α, гіпотеза відхиляється, коли вона справедлива.

Якщо гіпотезу Н₀ про взаємозв’язок ознак А і C відхиляти при

і не відхиляти в супротивному разі, то з імовірністю α, гіпотеза відхиляється, коли вона справедлива.

Якщо гіпотезу Н₀ про взаємозв’язок ознак В і C відхиляти при

і не відхиляти в супротивному разі, то з імовірністю α, гіпотеза відхиляється, коли вона справедлива.

Список використаних джерел

 

1.  Толстова Ю.Н. Анализ социологических данных: методология дескриптивная статистика, изучение связей между номинальными признаками, М.: Научный мир 2000.

2.  Елисеева И.И., Рукавишников В.О. Логика прикладного статистического

анализа. М.,: Финансы и статистика, 1982.

3.  Миркин Б.Г. Анализ качественных признаков и структур. М., 1980.

4.  Мирзоев А.А. Применение логлинейного анализа для обработки данных социологических исследований, М.: АН СССР, 1980.