Показатели численности и движения трудовых ресурсов
Правила построения рядов динамики
Показатели анализа ряда динамики
Методы анализа основной тенденции развития
Методы изучения сезонных колебаний
Ошибку выборки средней численности работников и границы, в которых будет находиться средняя численность работников в генеральной совокупности
Выявление наличия корреляционной связи между признаками, установление направления связи и измерение ее тесноты
Аналитическая часть
Навигация
Ошибку выборки средней численности работников и границы, в которых будет находиться средняя численность работников в генеральной совокупности
Статистические методы анализа динамики численности работников
63388
знаков
34
таблицы
12
изображений
1. Ошибку выборки средней численности работников и границы, в которых будет находиться средняя численность работников в генеральной совокупности.
2. Ошибку выборки доли организаций со среднесписочной численностью работников 180 чел. и более и границы, в которых будет находиться генеральная доля.
Задание 4
Имеются следующие данные о внутригодовой динамике численности работников организации по кварталам за три года, чел.:
| Кварталы | 2000 | 2001 | 2002 |
| I | 150 | 145 | 140 |
| II | 138 | 124 | 112 |
| III | 144 | 130 | 124 |
| IV | 152 | 150 | 148 |
Проведите анализ внутригодовой динамики численности работников организации, для чего:
1. Определите индексы сезонности методом постоянной средней.
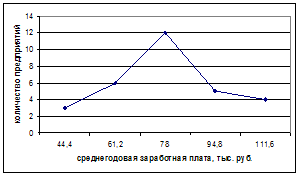
2. Изобразите на графике сезонную волну изменения численности работников. Сделайте выводы.
3. Осуществите прогноз численности работников организации на 2003 г. по кварталам на основе рассчитанных индексов сезонности при условии, что среднегодовая численность работников в прогнозируемом году составит 160 человек.
2.1. Исследование структуры совокупности
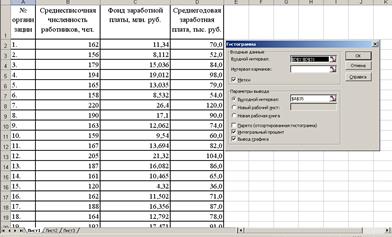
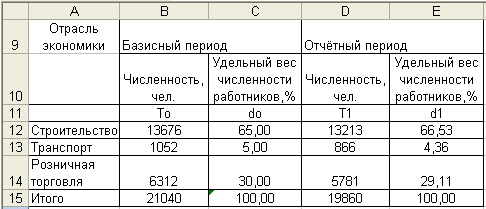
Для построения ряда распределения необходимо определить признак - среднесписочная численность работников (таблица 2.1.).
Таблица 2.1.: Исходные данные
| № п/п | Среднеспис. численность чел.(У) |
| 1 | 162 |
| 2 | 156 |
| 3 | 179 |
| 4 | 194 |
| 5 | 165 |
| 6 | 158 |
| 7 | 220 |
| 8 | 190 |
| 9 | 163 |
| 10 | 159 |
| 11 | 167 |
| 12 | 205 |
| 13 | 187 |
| 14 | 161 |
| 15 | 120 |
| 16 | 162 |
| 17 | 188 |
| 18 | 164 |
| 19 | 192 |
| 20 | 130 |
| 21 | 159 |
| 22 | 162 |
| 23 | 193 |
| 24 | 158 |
| 25 | 168 |
| 26 | 208 |
| 27 | 166 |
| 28 | 207 |
| 29 | 161 |
| 30 | 186 |
Таблица 2.2.: Отсортированные данные
| № п/п | Среднеспис. численность чел.(У) |
| 1 | 120 |
| 2 | 130 |
| 3 | 156 |
| 4 | 158 |
| 5 | 158 |
| 6 | 159 |
| 7 | 159 |
| 8 | 161 |
| 9 | 161 |
| 10 | 162 |
| 11 | 162 |
| 12 | 162 |
| 13 | 163 |
| 14 | 164 |
| 15 | 165 |
| 16 | 166 |
| 17 | 167 |
| 18 | 168 |
| 19 | 179 |
| 20 | 186 |
| 21 | 187 |
| 22 | 188 |
| 23 | 190 |
| 24 | 192 |
| 25 | 193 |
| 26 | 194 |
| 27 | 205 |
| 28 | 207 |
| 29 | 208 |
| 30 | 220 |
Ряд распределения – это группировка, представляющая собой распределение численности единиц совокупности по значению какого-либо признака, в настоящем случае по признаку – среднесписочная численность работников. Если ряд построен по количественному признаку, его называют вариационным. При построении вариационного ряда с равными интервалами определяют число групп (n) и величину интервала (h). По условию задачи необходимо образовать пять групп (n=5). Величина равного интервала рассчитывается по формуле:
,
где ymax и ymin – максимальное и минимальное значения признака.
чел.
Величина интервала равна 20,0. Отсюда путем прибавления величины интервала к минимальному уровню признака в группе получим следующие группы организаций по среднесписочной численности (таблица 2.3.).
Таблица 2.3.
| № интервала | Группа организаций | Число п/п | |
| в абсолютном выражении | в относительном выражении | ||
| 1 | 120 - 140 | 2 | 6,7% |
| 2 | 140 - 160 | 5 | 16,7% |
| 3 | 160 - 180 | 12 | 40,0% |
| 4 | 180 - 200 | 7 | 23,3% |
| 5 | 200 - 220 | 4 | 13,3% |
| Итого | 30 | 100,0% | |
Данные группировки показывают, что 63,3 % организаций имеют среднесписочную численность работников менее 180 чел.
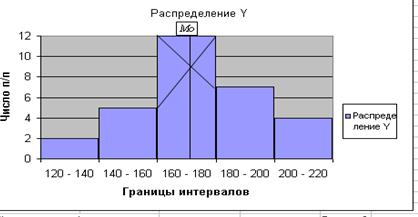
Мода (Мо) – это значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду – это вариант, имеющий наибольшую частоту. В интервальном вариационном ряду мода вычисляется по формуле:
,
где y0 – нижняя граница модального интервала;
h – размер модального интервала;
fMo – частота модального интервала;
fMo-1 – частота интервала, стоящего перед модальной частотой;
fMo+1 – частота интервала, стоящего после модальной частоты.
Отсюда: 
чел.
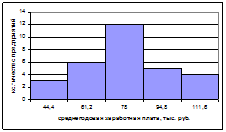
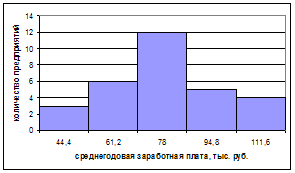
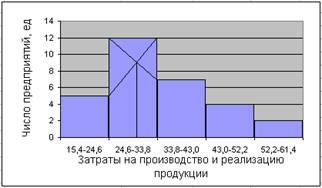
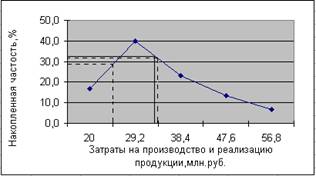
Графическое нахождение моды:
Медиана (Ме) – это величина признака, который находится в середине ранжированного ряда, то есть расположенного в порядке возрастания или убывания.
Для интервального вариационного ряда Ме рассчитывается по формуле: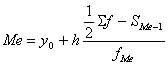 
,
где y0 – нижняя граница медианного интервала;
h – размер медианного интервала;
- половина от общего числа наблюдений;
SMe-1 – сумма наблюдений, накопленная до начала медианного интервала;
fMe – частота медианного интервала.
Определяем медианный интервал, в котором находится порядковый номер медианы (n).
В графе «Сумма накопленных наблюдений» таблицы 2.4. значение 15 соответствует интервалу №3, то есть 160 – 180. Это и есть медианный интервал, в котором находится медиана.
Отсюда: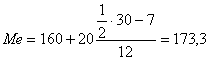 
чел.
Таблица 2.4.
| № интервала | Группа п/п | Число п/п | Сумма накопленных частот (S) | Середина интервала, Yi | |
| в абсолютном выражении | в относительном выражении | ||||
| 1 | 120 - 140 | 2 | 6,7% | 2 | 130 |
| 2 | 140 - 160 | 5 | 16,7% | 2 + 5 = 7 | 150 |
| 3 | 160 - 180 | 12 | 40,0% | 7 + 12 = 19 | 170 |
| 4 | 180 - 200 | 7 | 23,3% | 19 + 7 = 26 | 190 |
| 5 | 200 - 220 | 4 | 13,3% | 26 + 4 =30 | 210 |
| Итого | 30 | 100,0% |
| ||
Графическое нахождение медианы:
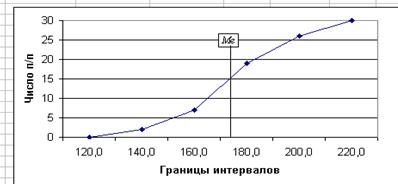
Рассчитаем характеристики ряда распределения.
Для расчета необходимо определить середины интервалов распределения среднесписочной численности работников (таблица 2.5.).
Таблица 2.5.
| Группа организаций | Середина интервала, Yi | Число п/п Ni | Yi * Ni | Yi - Ycp | (Yi - Ycp)2 * Ni |
| 120 - 140 | 130 | 2 | 260 | -44 | 3872 |
| 140 - 160 | 150 | 5 | 750 | -24 | 2880 |
| 160 - 180 | 170 | 12 | 2040 | -4 | 192 |
| 180 - 200 | 190 | 7 | 1330 | 16 | 1792 |
| 200 - 220 | 210 | 4 | 840 | 36 | 5184 |
| Итого | 30 | 5220 | 13920 |
Средняя арифметическая взвешенная определяется по формуле:
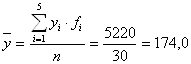чел., где
y – варианты или середины интервалов вариационного ряда;
f – соответствующая частота;
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и равно:
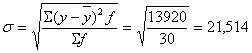чел.
То есть в среднем среднесписочная численность работников по организациям колеблется в пределах ± 21,514 чел. от его среднего значения 174,0 чел.
Коэффициент вариации представляет собой процентное отношение среднего квадратического отклонения к средней арифметической:
На основании полученного коэффициента вариации можно сделать вывод, что по уровню среднесписочной численности работников организации являются однородными, так как коэффициент не превышает 33%.
Вычислим среднюю арифметическую по исходным данным таблицы 1. Средняя арифметическая простая равна сумме значений признака, деленной на их число:
,
где y – значение признака;
n – число единиц признака.
чел.
Расхождения между арифметической средней простой и взвешенной возникли из-за того, что арифметическая средняя взвешенная считалась по сгруппированным данным.
Похожие работы
... по чистой продукции, которая определяется путем вычитания из товарной продукции материальных затрат и суммы амортизации основных фондов, что в условиях рынка соответствует понятию «валовой доход». 1.3 Статистические методы анализа динамики объема производства продукции и услуг на предприятии (фирме) В статистическом изучении динамики объема производства продукции и услуг на предприятии ...
... на определенный момент времени. В интервальном ряду динамики уровни ряда представлены за период времени. 1.2 Статистические методы анализа динамики объема производства продукции и услуг В статистическом изучении динамики объема производства продукции и услуг на предприятии можно использовать различные методы. Статистическое исследование динамического ряда объема производства продукции и ...
... из одной единицы, обладающей всем объёмом признака. Минимальное значение приближается к нулю, но его никогда ни достигает. [2; 135] 2. Расчётная часть 2.1. Условие задач Для анализа финансовых результатов деятельности предприятий одной из отраслей экономики произведена 10% -ная механическая выборка, в результате которой получены следующие данные млн. руб.: № предприятия п/п ...
... при анализе различных явлений, относящихся к одному и тому же объекту. Раздел 2. Методы анализа рядов динамики 2.1 Понятие о статистических рядах динамики Методы анализа рядов динамики занимают немаловажное место в связи с тем, что уровни общественных явлений изменяются во времени и, следовательно, необходимо выделить однородные этапы развития, найти и охарактеризовать свойственные им ...
0 комментариев