Показатели численности и движения трудовых ресурсов
Правила построения рядов динамики
Показатели анализа ряда динамики
Методы анализа основной тенденции развития
Методы изучения сезонных колебаний
Ошибку выборки средней численности работников и границы, в которых будет находиться средняя численность работников в генеральной совокупности
Выявление наличия корреляционной связи между признаками, установление направления связи и измерение ее тесноты
Аналитическая часть
Навигация
Выявление наличия корреляционной связи между признаками, установление направления связи и измерение ее тесноты
Статистические методы анализа динамики численности работников
63388
знаков
34
таблицы
12
изображений
2.2. Выявление наличия корреляционной связи между признаками, установление направления связи и измерение ее тесноты
Необходимо определить признак – среднегодовая стоимость ОПФ.
Таблица 2.6.: Исходные данные
| № п/п | Стоимость ОПФ млн.руб.(Х) |
| 1 | 34,714 |
| 2 | 24,375 |
| 3 | 41,554 |
| 4 | 50,212 |
| 5 | 38,347 |
| 6 | 27,408 |
| 7 | 60,923 |
| 8 | 47,172 |
| 9 | 37,957 |
| 10 | 30,210 |
| 11 | 38,562 |
| 12 | 52,500 |
| 13 | 45,674 |
| 14 | 34,388 |
| 15 | 16,000 |
| 16 | 34,845 |
| 17 | 46,428 |
| 18 | 38,318 |
| 19 | 47,590 |
| 20 | 19,362 |
| 21 | 31,176 |
| 22 | 36,985 |
| 23 | 48,414 |
| 24 | 28,727 |
| 25 | 39,404 |
| 26 | 55,250 |
| 27 | 38,378 |
| 28 | 55,476 |
| 29 | 34,522 |
| 30 | 44,839 |
Таблица 2.7.: Отсортированные данные
| № п/п | Стоимость ОПФ млн.руб.(Х) |
| 1 | 16,000 |
| 2 | 19,362 |
| 3 | 24,375 |
| 4 | 27,408 |
| 5 | 28,727 |
| 6 | 30,210 |
| 7 | 31,176 |
| 8 | 34,388 |
| 9 | 34,522 |
| 10 | 34,714 |
| 11 | 34,845 |
| 12 | 36,985 |
| 13 | 37,957 |
| 14 | 38,318 |
| 15 | 38,347 |
| 16 | 38,378 |
| 17 | 38,562 |
| 18 | 39,404 |
| 19 | 41,554 |
| 20 | 44,839 |
| 21 | 45,674 |
| 22 | 46,428 |
| 23 | 47,172 |
| 24 | 47,590 |
| 25 | 48,414 |
| 26 | 50,212 |
| 27 | 52,500 |
| 28 | 55,250 |
| 29 | 55,476 |
| 30 | 60,923 |
Построим интервальный ряд, характеризующий распределение организаций по среднегодовой стоимости ОПФ, образовав пять групп с равными интервалами (таблица 2.8.).
млн. руб.
Таблица 2.8.
| Группа организаций | Число п/п | |
| в абсолютном выражении | в относительном выражении | |
| 16,000 - 24,984 | 3 | 10,0% |
| 24,984 - 33,969 | 4 | 13,3% |
| 33,969 - 42,954 | 12 | 40,0% |
| 42,954 - 51,938 | 7 | 23,3% |
| 51,938 - 60,923 | 4 | 13,3% |
| Итого | 30 | 100,0% |
Корреляционная таблица – это специальная комбинационная таблица, в которой представлена группировка по двум взаимосвязанным признакам: факторному и результативному. Необходимо определить, существует ли зависимость между среднегодовой стоимостью ОПФ и среднесписочной численностью работников. Построим корреляционную таблицу, образовав пять групп по факторному и результативному признакам (таблица 2.9.).
Совмещая данные по Х и Y получим следующую группировку: «Аналитическая группировка (по двум признакам)».
Таблица 2.9.
| Центр.значение, Ycp(j) | 130 | 150 | 170 | 190 | 210 | Nj | ||||||
| Группы по Х | Группы по У | 120 | 140 | 140 | 160 | 160 | 180 | 180 | 200 | 200 | 220 | |
| 16,000 | 24,985 | 2 | 1 | 3 | ||||||||
| 24,985 | 33,969 | 4 | 4 | |||||||||
| 33,969 | 42,954 | 12 | 12 | |||||||||
| 42,954 | 51,938 | 7 | 7 | |||||||||
| 51,938 | 60,923 | 4 | 4 | |||||||||
| 16,000 | 24,985 | 2 | 5 | 12 | 7 | 7 | 30 | |||||
Как видно из данных таблицы 2.9., распределение числа субъектов произошло вдоль диагонали, проведенной из левого верхнего угла в правый нижний угол таблицы, то есть увеличение признака «Среднегодовая стоимость ОПФ» сопровождалось увеличением признака «Среднесписочная численность работников». Характер концентрации частот по диагонали корреляционной таблицы свидетельствует о наличии прямой тесной корреляционной связи между изучаемыми признаками.
Аналитическая группировка позволяет изучать взаимосвязь факторного и результативного признаков. Установим наличие и характер связи между среднегодовой стоимостью ОПФ и среднесписочной численностью работников методом аналитической группировки (таблица 2.10.).
Таблица 2.10.
| Группа п/п | Число п/п | Х | У | ||
| Всего по группе | В среднем | Всего по группе | В среднем | ||
| 16 - 24,985 | 3 | 59,737 | 19,912 | 406,000 | 135,333 |
| 24,985 - 33,969 | 4 | 117,521 | 29,380 | 634,000 | 158,500 |
| 33,969 - 42,954 | 12 | 447,974 | 37,331 | 1980,000 | 165,000 |
| 42,954 - 51,938 | 7 | 330,329 | 47,190 | 1330,000 | 190,000 |
| 51,938 - 60,923 | 4 | 224,149 | 56,037 | 840,000 | 210,000 |
| Итого | 30 | 1179,710 | 39,324 | 5190,000 | 173,000 |
Данные таблицы 2.10. показывают, что с ростом среднесписочной численности работников среднегодовая стоимость ОПФ увеличивается. Следовательно, между исследуемыми признаками существует прямая корреляционная связь.
Вычислим коэффициент детерминации и эмпирическое корреляционное отношение, для чего выполним некоторые расчеты.
Таблица 8: Исходные данные и расчет коэффициента детерминации
| № | Х | У | (У - Уср)2 | (X - Xср)2 | (У - Уср)*(X - Xср) | n | |
| 1 | 16,000 | 120 | 2809,0 | 544,0 | 1236,2 | ||
| 2 | 19,362 | 130 | 1849,0 | 398,5 | 858,4 | ||
| 3 | 24,375 | 156 | 289,0 | 223,5 | 254,1 | ||
| 1 группа | 59,737 | 406,0 |
|
|
| 3 | |
| 19,912 | 135,3 |
|
|
| |||
| 4 | 27,408 | 158 | 225,0 | 142,0 | 178,7 | ||
| 5 | 28,727 | 158 | 225,0 | 112,3 | 159,0 | ||
| 6 | 30,210 | 159 | 196,0 | 83,1 | 127,6 | ||
| 7 | 31,176 | 159 | 196,0 | 66,4 | 114,1 | ||
| 2 группа | 117,521 | 634,0 |
|
|
| 4 | |
| 29,380 | 158,5 |
|
|
| |||
| 8 | 34,388 | 161 | 144,0 | 24,4 | 59,2 | ||
| 9 | 34,522 | 161 | 144,0 | 23,1 | 57,6 | ||
| 10 | 34,714 | 162 | 121,0 | 21,2 | 50,7 | ||
| 11 | 34,845 | 162 | 121,0 | 20,1 | 49,3 | ||
| 12 | 36,985 | 162 | 121,0 | 5,5 | 25,7 | ||
| 13 | 37,957 | 163 | 100,0 | 1,9 | 13,7 | ||
| 14 | 38,318 | 164 | 81,0 | 1,0 | 9,1 | ||
| 15 | 38,347 | 165 | 64,0 | 1,0 | 7,8 | ||
| 16 | 38,378 | 166 | 49,0 | 0,9 | 6,6 | ||
| 17 | 38,562 | 167 | 36,0 | 0,6 | 4,6 | ||
| 18 | 39,404 | 168 | 25,0 | 0,0 | -0,4 | ||
| 19 | 41,554 | 179 | 36,0 | 5,0 | 13,4 | ||
| 3 группа | 447,974 | 1980,0 |
|
|
| 12 | |
| 37,331 | 165,0 |
|
|
| |||
| 20 | 44,839 | 186 | 169,0 | 30,4 | 71,7 | ||
| 21 | 45,674 | 187 | 196,0 | 40,3 | 88,9 | ||
| 22 | 46,428 | 188 | 225,0 | 50,5 | 106,6 | ||
| 23 | 47,172 | 190 | 289,0 | 61,6 | 133,4 | ||
| 24 | 47,590 | 192 | 361,0 | 68,3 | 157,1 | ||
| 25 | 48,414 | 193 | 400,0 | 82,6 | 181,8 | ||
| 26 | 50,212 | 194 | 441,0 | 118,6 | 228,7 | ||
| 4 группа | 330,329 | 1330,0 |
|
|
| 7 | |
| 47,190 | 190,0 |
|
|
| |||
| 27 | 52,500 | 205 | 1024,0 | 173,6 | 421,6 | ||
| 28 | 55,250 | 208 | 1225,0 | 253,6 | 557,4 | ||
| 29 | 55,476 | 207 | 1156,0 | 260,9 | 549,2 | ||
| 30 | 60,923 | 220 | 2209,0 | 466,5 | 1015,2 | ||
| 5 группа | 224,149 | 840,0 |
|
|
| 4 | |
| 56,037 | 210,0 |
|
|
| |||
| Все группы | 1179,710 | 5190,0 | 14526,0 | 3281,2 | 6736,7 | 30 | |
| 39,324 | 173,0 |
|
|
|
Коэффициент детерминации
Таблица 9: Исходные данные и расчет эмпирического корреляционного отношения
| Группа п/п | Число п/п, nj | Для расчета межгрупповой дисперсии | |||
| Усрj | (Усрj - Уср)2 | (Усрj - Уср)2 * nj | |||
| 16 - 24,985 | 3 | 135,333 | 1418,778 | 4256,333 | = 1418,778 * 3 |
| 24,985 - 33,969 | 4 | 158,500 | 210,250 | 841,000 | = 210,25 * 4 |
| 33,969 - 42,954 | 12 | 165,000 | 64,000 | 768,000 | = 64 * 12 |
| 42,954 - 51,938 | 7 | 190,000 | 289,000 | 2023,000 | = 289 * 7 |
| 51,938 - 60,923 | 4 | 210,000 | 1369,000 | 5476,000 | = 1369 * 4 |
| Итого | 30 | 173,000 | 13364,333 | ||
Межгрупповая дисперсия
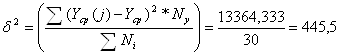
Общая дисперсия
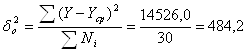
Эмпирическое корреляционное отношение
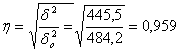
Коэффициент детерминации показывает, что на 97,6% фактор Х обусловлен фактором Y. Расчетное показывает сильную линейную связь между Х и Y. Эмпирическое корреляционное отношение показывает общую тесноту связи между Х и Y. Расчетное значение показывает сильную тесноту связи.
Задание 3
Решение
n/N = 0,20 (выборка 20%-ная, бесповторная)
Среднеквадратическое отклонение 
чел.
Т.к. р (вероятность) = 0,954, то t = 2.
Предельная ошибка бесповторной выборки
Тогда искомые границы для среднего значения ген совокупности:
Искомая доля: 
Тогда предельная ошибка выборки для доли
Тогда искомые границы для доли
Генеральная доля находится в границах (0,209 ; 0,524)
Задание 4
Имеются следующие данные о внутригодовой динамике численности работников организации по кварталам за три года, чел.
| Кварталы | 2000 | 2001 | 2002 |
| I | 150 | 145 | 140 |
| II | 138 | 124 | 112 |
| III | 144 | 130 | 124 |
| IV | 152 | 150 | 148 |
Проведите анализ внутригодовой динамики численности работников организации, для чего:
4. Определите индексы сезонности методом постоянной средней.
5. Изобразите на графике сезонную волну изменения численности работников. Сделайте выводы.
6. Осуществите прогноз численности работников организации на 2003 г. по кварталам на основе рассчитанных индексов сезонности при условии, что среднегодовая численность работников в прогнозируемом году составит 160 человек.
Решение
Рассчитаем средне значение численности работников, чел.
| 584,0 | ||||
| В среднем за 2000г. | Icp2000 = | -------------- = | 146,0 | |
| 4 кв. | ||||
| 549,0 | ||||
| В среднем за 2001г. | Icp2001 = | -------------- = | 137,3 | |
| 4 кв. | ||||
| 524,0 | ||||
| В среднем за 2002г. | Icp2002 = | -------------- = | 131,0 | |
| 4 кв. | ||||
| 600,0 | ||||
| В среднем за 2003г. | Icp2003 = | -------------- = | 150,0 | |
| 4 кв. | ||||
Рассчитаем индексы сезонности, например для 2000г.
| 150,0 | ||||
| I кв. | II2000 = | -------------- = | 1,027 | |
| 146,0 | ||||
| 138,0 | ||||
| II кв. | III2000 = | -------------- = | 0,945 | |
| 146,0 | ||||
| 144,0 | ||||
| III кв. | IIII2000 = | -------------- = | 0,986 | |
| 146,0 | ||||
| 152,0 | ||||
| IV кв. | IIV2000 = | -------------- = | 1,041 | |
| 146,0 |
Рассчитаем средний индекс сезонности методом простой средней:
| 1,027 + 1,056 + 1,069 | ||||
| I кв. | IcpI = | ---------------------------- = | 1,051 | |
| 3 | ||||
| 0,945 + 0,903 + 0,855 | ||||
| II кв. | IcpII = | ---------------------------- = | 0,901 | |
| 3 | ||||
| 0,986 + 0,947 + 0,947 | ||||
| III кв. | IcpIII = | ---------------------------- = | 0,960 | |
| 3 | ||||
| 1,041 + 1,093 + 1,130 | ||||
| IV кв. | IcpIV = | ---------------------------- = | 1,088 | |
| 3 |
Численность работников в 2003г (прогноз), чел.
|
|
|
|
|
|
|
| I кв. | II2003 = | 150,0 | * 1,051 = | 157,6 | |
| II кв. | III2003 = | 150,0 | * 0,901 = | 135,2 | |
| III кв. | IIII2003 = | 150,0 | * 0,960 = | 144,0 | |
| IV кв. | IIV2003 = | 150,0 | * 1,088 = | 163,2 | |
В итоге получим таблицу индексов сезонности
| Квартал | Индексы сезонности | ||||
| 2000г. | 2001г. | 2002г. | В среднем за 3 года | 2003г. (прогноз) | |
| I | 1,027 | 1,056 | 1,069 | 1,051 | 1,051 |
| II | 0,945 | 0,903 | 0,855 | 0,901 | 0,901 |
| III | 0,986 | 0,947 | 0,947 | 0,960 | 0,960 |
| IV | 1,041 | 1,093 | 1,130 | 1,088 | 1,088 |
В итоге получим таблицу динамики численности в 2003г., чел.
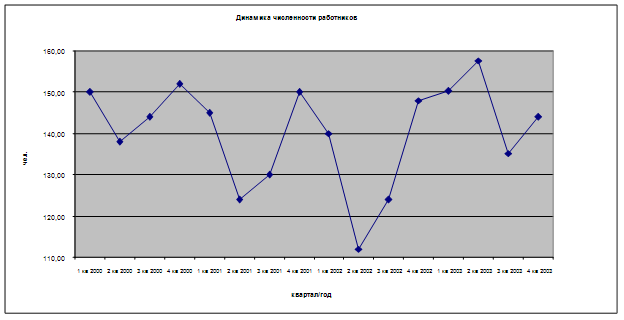
| Квартал | Динамика численности работников, чел. | ||||
| 2000г. | 2001г. | 2002г. | В среднем за 3 года | 2003г. (прогноз) | |
| I | 150 | 145 | 140 | 145,1 | 157,6 |
| II | 138 | 124 | 112 | 124,4 | 135,2 |
| III | 144 | 130 | 124 | 132,6 | 144,0 |
| IV | 152 | 150 | 148 | 150,2 | 163,2 |
| Итого | 584 | 549 | 524 | 552,3 | 600,0 |
| В среднем за квартал | 146,0 | 137,3 | 131,0 | 138,1 | 150,0 |
Изобразим графически результаты вычислений
Похожие работы
... по чистой продукции, которая определяется путем вычитания из товарной продукции материальных затрат и суммы амортизации основных фондов, что в условиях рынка соответствует понятию «валовой доход». 1.3 Статистические методы анализа динамики объема производства продукции и услуг на предприятии (фирме) В статистическом изучении динамики объема производства продукции и услуг на предприятии ...
... на определенный момент времени. В интервальном ряду динамики уровни ряда представлены за период времени. 1.2 Статистические методы анализа динамики объема производства продукции и услуг В статистическом изучении динамики объема производства продукции и услуг на предприятии можно использовать различные методы. Статистическое исследование динамического ряда объема производства продукции и ...
... из одной единицы, обладающей всем объёмом признака. Минимальное значение приближается к нулю, но его никогда ни достигает. [2; 135] 2. Расчётная часть 2.1. Условие задач Для анализа финансовых результатов деятельности предприятий одной из отраслей экономики произведена 10% -ная механическая выборка, в результате которой получены следующие данные млн. руб.: № предприятия п/п ...
... при анализе различных явлений, относящихся к одному и тому же объекту. Раздел 2. Методы анализа рядов динамики 2.1 Понятие о статистических рядах динамики Методы анализа рядов динамики занимают немаловажное место в связи с тем, что уровни общественных явлений изменяются во времени и, следовательно, необходимо выделить однородные этапы развития, найти и охарактеризовать свойственные им ...
0 комментариев