Производственный метод исчисления ВРП
Распределительный метод исчисления ВРП
Методы социально-экономического прогнозирования
Эконометрические модели прогнозирования
Анализ производства ВРП республики Бурятия
Выявление наличия тенденций
Выбор уравнения тренда
Прогнозирование на основе эконометрической модели
Навигация
Эконометрические модели прогнозирования
Статистический анализ и прогнозирование
69456
знаков
11
таблиц
12
изображений
2.2 Эконометрические модели прогнозирования
Объектом статистического изучения в социальных науках являются сложные системы. Измерение тесноты связей между переменными, построение изолированных уравнений регрессии недостаточны для описания таких систем и объяснения механизма их функционирования. Отдельно взятое уравнение множественной регрессии не может характеризовать истинные влияния отдельных признаков на вариацию результирующей переменной. Именно поэтому в экономических исследованиях важное место заняла проблема описания структуры связей между переменными системой так называемых одновременных уравнений или структурных уравнений. Например, модель национальной экономики включает в себя следующую систему уравнений: функции потребления, инвестиций, тождество доходов и т.д. Это связано с тем, что макроэкономические показатели, являясь обобщающими показателями состояния экономики, чаще всего взаимозависимы. Так, расходы на конечное потребление в экономике зависят от валового национального дохода. Вместе с тем величина валового национального дохода рассматривается как функция инвестиций.
Эконометрические модели описывают взаимообусловленное развитие социально-экономических процессов на основе информации, отражающей распределение их уровней во времени и в пространстве однородных объектов. Наиболее важной задачей является оценка и проверка экономической модели. Эконометрическое моделирование охватывает весь цикл решения экономической задачи – от ее постановки до содержательной интерпретации результатов статистического анализа и прогнозирования.
Классификация переменных в эконометрических моделях.
1. Эндогенные переменные, т.е экономические величины, которые являются зависимыми и объясняются эконометрической моделью.
2. Экзогенные переменные, определяемые вне модели. Они не объясняются моделью и являются внешними, заданными экономическими величинами.
3. Лаговые переменные, значения которых отстают на один или несколько периодов. Поскольку лаговые переменные в период времени t также не объясняются эконометрической моделью, то их можно отнести к заранее заданным экзогенным.
4. Предопределенные переменные, к которым относятся:
а.) обычные экзогенные переменные, они заранее предопределены, так как объясняются фактами, лежащими вне модели;
б.) лаговые экзогенные переменные, они заранее предопределены, так как их значения принадлежат предшествующим периодам и объясняются вне модели;
в.) лаговые эндогенные переменные, их предопределенность следует из предшествующего объяснения в эконометрической модели.
5. Совместно зависимые переменные, которые определяются не одним уравнением, а одновременными уравнениями модели.
6. Возмущающие переменные, т.е. экономические величины, не входящие в уравнения эконометрических моделей, но оказывающие влияние на совместно зависимые переменные.
Виды эконометрических моделей
В зависимости от цели исследования и поставленных задач эконометрическая модель может быть представлена в различных видах.
1. Структурная форма модели. Она отражает одно- и многосторонние стохастические причинные отношения между экономическими величинами в их непосредственном виде. Эта система уравнений, отражающих наличие одновременных экономических взаимосвязей, называется системой одновременных или структурных уравнений. В структурном уравнении содержится одна или несколько совместно зависимых переменных.
Наряду со структурными уравнениями эконометрическая модель может содержать так называемые определяющие уравнения – тождества. Тождества не содержат возмущений и их параметры в общем случае равны единице, следовательно, они не подлежат оценке. Примером может быть следующая модель:
;
;
.
2. Полная эконометрическая модель:
а.) она охватывает те переменные, которые оказывают существенное влияние на совместно зависимые переменные, а возмущения имеют случайный характер;
б.) она содержит столько уравнений, сколько в ней имеется совместно зависимых переменных;
в.) система уравнений имеет однозначное решение относительно совместных зависимых переменных.
Модель должна быть полной, когда необходимо количественно описать экономическое явление или когда она применяется для прогнозирования. Структурная форма важна при конструировании модели, при получении прогнозных значений и принятии решений главная роль принадлежит приведенной, или прогнозной форме.
3. Прогнозная, или приведенная форма эконометрической модели. В данном случае решается система линейных уравнений относительно эндогенных совместно зависимых переменных. Эти переменные являются линейными функциями от предопределенных и возмущающих переменных.
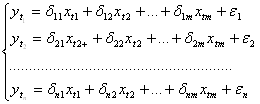
Коэффициенты уравнений в модели являются комбинациями всех структурных коэффициентов совместно зависимых переменных и соответствующих предопределенных переменных во всех структурных уравнениях.
4. Рекурсивная модель. Модель может быть представлена в следующем виде:
В данной системе линейных уравнений зависимая переменная одного уравнения является фактором в других уравнениях.
5. Модель из системы независимых уравнений. В системе каждая эндогенная переменная 
рассматривается как функция одного и того же набора факторов 
.
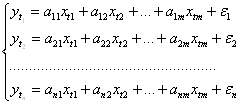
Эндогенные переменные независимы между собой, структурная и приведенная формы таких моделей совпадают.
Проблемы идентификации в эконометрических моделях
При изучении систем одновременных уравнений, описывающих взаимосвязи, каждое структурное уравнение должно быть проверено на идентифицируемость. Идентифицируемость структурных уравнений означает, что посредством линейной комбинации некоторых или всех уравнений модели невозможно получить ни одно уравнение, которое противоречило бы модели и параметры которого отличались бы от параметров структурных уравнений, подлежащих оценке.
Применяются следующие критерии идентифицируемости для полной эконометрической модели.
1. Необходимым, но не достаточным условием идентифицируемости модели является следующее требование-критерий: число предопределенных переменных (D), которые содержатся в модели, но исключены из рассматриваемого структурного уравнения, по крайней мере должно быть равно числу совместно зависимых (эндогенных) переменных (H) в этом же структурном уравнении минус единица.
Критерий можно записать так:
D ≥ H – 1.
При D = H – 1 имеет место точная идентификация, т.е. число ограничений на параметры модели достаточно, чтобы однозначно определять параметры структурных уравнений по их приведенной форме.
При D > H – 1 уравнение сверхидентифицируемо. В данном случае имеется больше ограничений на параметры модели, чем это необходимо для идентификации.
При D < H – 1 структурное уравнение неидентифицируемо, т.к. число ограничений является недостаточным.
2. Необходимое и достаточное условие идентифицируемости модели определяется на основе матрицы. Составленной из коэффициентов при переменных, исключенных из исследуемого уравнения. Ранг этой матрицы должен быть не менее числа совместно зависимых эндогенных переменных минус единица.
Идентификация структурных моделей предполагает, что возмущения распределены независимо друг от друга. Т.к. независимость возмущений является одним из требований рекурсивной модели, рекурсивные модели всегда идентифицируемы.
Оценивание параметров эконометрических моделей
Обыкновенный метод наименьших квадратов может применяться для оценивания параметров системы независимых уравнений, рекурсивных и моделей из взаимозависимых переменных.
Для решения идентифицируемых уравнений применяется косвенный метод наименьших квадратов. Обычный МНК не учитывает одновременных соотношений между совместно зависимыми переменными, поэтому не может непосредственно применяться.
Модель вначале представляется в прогнозной (приведенной) форме. Применяя МНК к каждому полученному уравнению, оценивают все параметры (коэффициенты) системы в прогнозной форме. Так как по предположению все структурные уравнения точно идентифицируемы, на следующем этапе однозначно определяются структурные коэффициенты по коэффициентам прогнозных уравнений. То есть структурные коэффициенты оцениваются косвенно через оценки параметров прогнозной модели.
Для решения сверхидентифицированных уравнений применяется двухшаговый метод наименьших квадратов, учитывающий многосторонние связи совместно зависимых переменных. В данном случае структурные уравнения содержат меньше коэффициентов, чем приведенные.
Метод является обобщением обычного МНК и выполняется в два этапа. Основная идея двухшагового МНК заключается в замене зависимых переменных на их оценки 
. Благодаря этому содержащиеся в уравнениях переменные приобретают характер предопределенных переменных и применение МНК дает удовлетворительные оценки.
Алгоритм метода включает следующие шаги:
1. Структурные уравнения преобразовываются в приведенные.
2. Приведенные уравнения решаются с помощью МНК.
3. Проверяется надежность уравнений по F-критерию.
4. Если уравнения надежны, по ним вычисляются расчетные значения эндогенных переменных для каждой единицы совокупности.
5. Эти расчетные значения эндогенных переменных, находящихся в правой части структурных уравнений, и соответствующие значения экзогенных переменных используются для решения структурных уравнений с помощью МНК.
6. Вновь проверяется надежность полученных решений. Эта проверка необходима, так как при ДМНК решенные структурные уравнения качественно отличны от приведенных уравнений, в том числе имеют другое число степеней свободы вариации, поэтому надежность приведенных уравнений еще не гарантирует надежность решения структурных уравнений.
Похожие работы
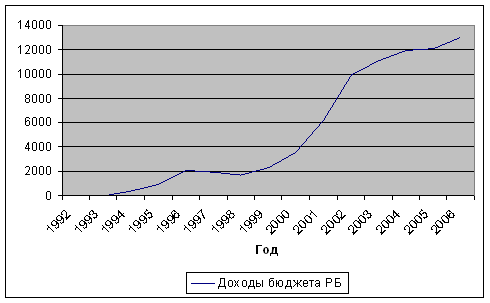
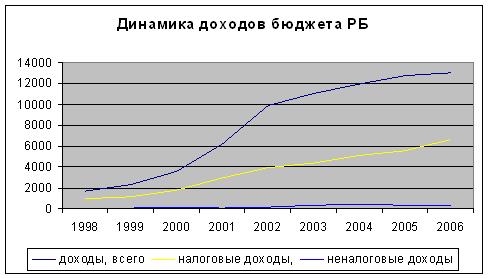
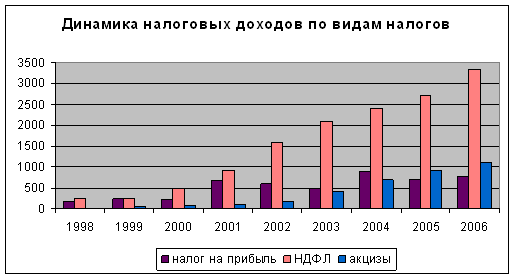
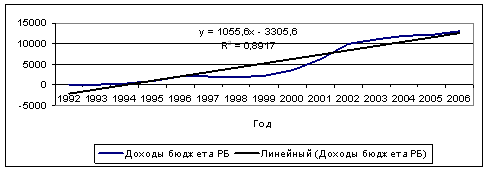
... анализ, а также необходимо использование специальных методов прогнозирования временных рядов. 2 глава. Экономико-математические методы статистического анализа и прогнозирования доходов бюджета региона 2.1 Методы статистического анализа доходов бюджета региона Для количественной оценки динамики доходов бюджета региона применяются статистические показатели: абсолютные темпы роста и ...
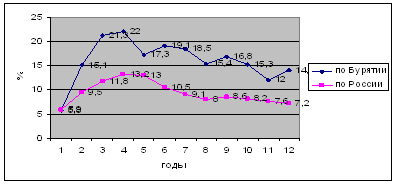
... с методологией МОТ классифицируются как безработные. Прежде всего, дается информация об абсолютной численности безработных в стране и по регионам. Глава 3. Экономико–статистический анализ и прогнозирование безработицы 3.1. Экономический анализ безработицы Привычным явлением для некоторых категорий населения стала безработица. В 2005 году из общей численности трудовых ресурсов 252,4 тыс. ...
... найденное значение среднего темпа роста выступает в качестве коэффициента для составления прогноза на будущий срок. Высчитывается по формуле: (1.26) 2. Статистический показатель расчетов временных рядов (корреляция) Случайной величиной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин ...
... анализировать их тенденции и прогнозировать ситуацию в будущем. Все участники рынка ценных бумаг планируют свои операции только после тщательного анализа. Статистические методы прогнозирования развития рынка ценных бумаг основаны на построении фондовых индексов, расчете показателей дисперсии, вариации, ковариации, экстраполяции и интерполяции. Фондовые индексы являются самыми популярными во всём ...
0 комментариев