Навигация
Выбор уравнения тренда
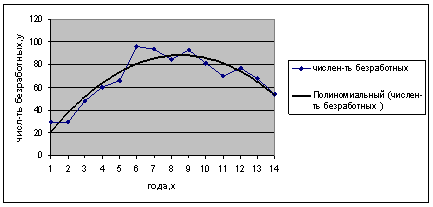
3.6 Выбор уравнения тренда
Для отображения основной тенденции развития явлений во времени применяются полиномы разной степени, экспоненты, логистические кривые и другие функции. В статистической практике параметры полиномов невысокой степени иногда имеют конкретную интерпретацию характеристик динамического ряда. Так, параметр ![]() трактуется как характеристика средних условий ряда динамики, параметры
трактуется как характеристика средних условий ряда динамики, параметры ![]() ,
, ![]() ,
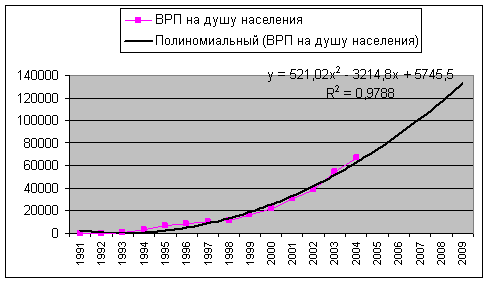
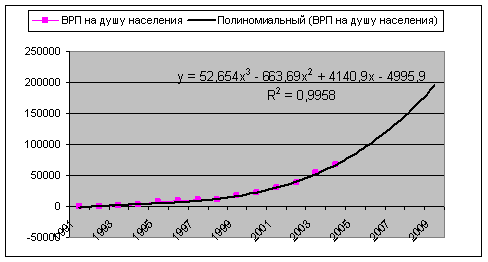
, ![]() - изменения ускорения. В статистике выработано правило выбора степени полинома модели развития, основанное на определении величин конечных разностей уровней динамических рядов. Согласно этому правилу полином первой степени (прямая) применяется как модель такого ряда динамики, у которого первые разности (абсолютные приросты) постоянны; полиномы 2-й степени – для отражения ряда динамики с постоянными вторыми разностями (ускорениями); полиномы 3-й степени – с постоянными третьими разностями и т.д. Для полиномиальных моделей характерно отсутствие прямой связи между абсолютными приростами и приростами уровней рядов динамики.
- изменения ускорения. В статистике выработано правило выбора степени полинома модели развития, основанное на определении величин конечных разностей уровней динамических рядов. Согласно этому правилу полином первой степени (прямая) применяется как модель такого ряда динамики, у которого первые разности (абсолютные приросты) постоянны; полиномы 2-й степени – для отражения ряда динамики с постоянными вторыми разностями (ускорениями); полиномы 3-й степени – с постоянными третьими разностями и т.д. Для полиномиальных моделей характерно отсутствие прямой связи между абсолютными приростами и приростами уровней рядов динамики.
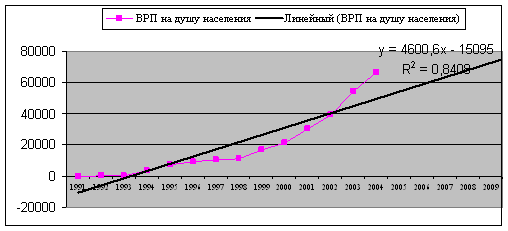
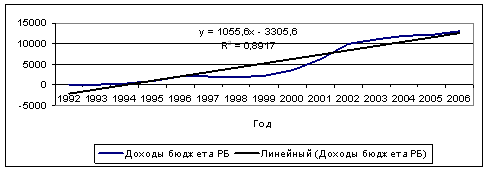
Линейная функция. Параметры линейного тренда можно интерпретировать так: а – начальный уровень временного ряда в момент времени t = 0; b – средний за период абсолютный прирост уровней ряда. Применительно к данному временному ряду можно сказать, что средний за год абсолютный прирост равен 4600,56 рублей.
У=-15095,5+4600,56t
R^2=0,84
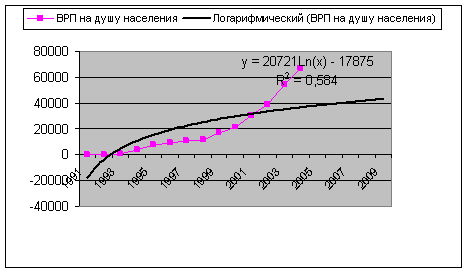
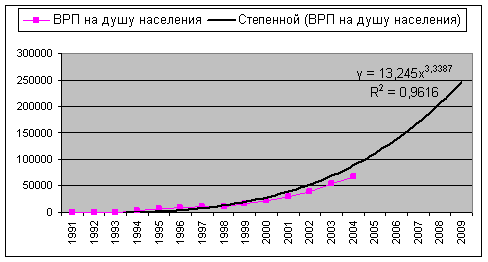
Параметры экспоненциального тренда имеют следующую интерпретацию. Параметр а – это начальный уровень временного ряда в момент времени t = 0. Величина ![]() – это средний за единицу времени коэффициент роста уровней ряда. Средний за год цепной темп прироста временного ряда составил 73,2%.
– это средний за единицу времени коэффициент роста уровней ряда. Средний за год цепной темп прироста временного ряда составил 73,2%.
3.7 Экспоненциальное сглаживание
В настоящее время для учета степени «устаревания» данных во взвешенных скользящих средних используются веса, подчиняющиеся экспоненциальному закону, т.е. применяется метод экспоненциальных средних. Смысл экспоненциальных средних состоит в том, чтобы найти такие средние, в которых влияние прошлых наблюдений затухает по мере удаления от момента, для которого определяются средние. Веса в экспоненциальных средних устанавливаются в виде коэффициентов α (ΙαΙ < 1). Веса по времени убывают экспоненциально, а сумма весов стремится к 1. В качестве весов используется ряд:
![]() ;
; ![]() ;
; ![]() ;
; ![]() и т.д.
и т.д.
Экспоненциальная средняя определяется по формуле Р. Брауна:
![]() ,
,
где ![]() – экспоненциальная средняя (сглаженное значение уровня ряда) на момент t; α – вес текущего наблюдения при расчете экспоненциальной средней;
– экспоненциальная средняя (сглаженное значение уровня ряда) на момент t; α – вес текущего наблюдения при расчете экспоненциальной средней; ![]() –фактический уровень динамического ряда в момент времени t;
–фактический уровень динамического ряда в момент времени t; ![]() –экспоненциальная средняя предыдущего периода.
–экспоненциальная средняя предыдущего периода.
Как видно из формулы, сглаженный по экспоненциальной средней уровень динамического ряда есть не что иное, как линейная комбинация двух величин: фактического уровня динамического ряда на момент времени t, т.е. ![]() , и среднего уровня (
, и среднего уровня (![]() ), рассчитанного для предыдущего периода. Таким образом, экспоненциальная средняя (
), рассчитанного для предыдущего периода. Таким образом, экспоненциальная средняя (![]() ) формируется под влиянием всех предшествующих уровней ряда от его начала до момента t включительно.
) формируется под влиянием всех предшествующих уровней ряда от его начала до момента t включительно.
Вес, с которым участвует каждый уровень динамического ряда в определении экспоненциальных средних, зависит от параметра сглаживания ![]() . Поэтому при использовании экспоненциальных средних в прогнозировании одной из важных проблем является выбор оптимального значения параметра
. Поэтому при использовании экспоненциальных средних в прогнозировании одной из важных проблем является выбор оптимального значения параметра ![]() .
.
Если коэффициент ![]() близок к 0, то веса, по которым взвешиваются уровни динамического ряда, убывают медленно, и при прогнозе в этом случае учитываются все прошлые наблюдения. Если
близок к 0, то веса, по которым взвешиваются уровни динамического ряда, убывают медленно, и при прогнозе в этом случае учитываются все прошлые наблюдения. Если ![]() близок к 1, то при прогнозировании учитываются в основном наблюдения последних лет, чем ближе
близок к 1, то при прогнозировании учитываются в основном наблюдения последних лет, чем ближе ![]() к 1, тем в большей мере сглаженные уровни воспроизводят фактические уровни динамического ряда.
к 1, тем в большей мере сглаженные уровни воспроизводят фактические уровни динамического ряда.
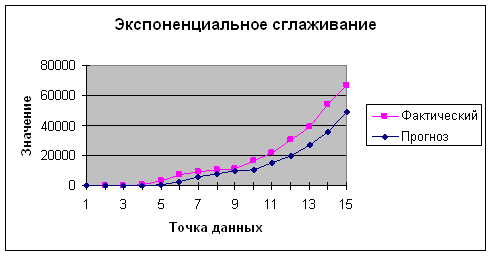
Экспоненциальное сглаживание при разных значениях параметра ![]()
| Года | у | Экспоненциальные средние при α | ||||
| α=0,1 | α=0,3 | α=0,5 | α=0,7 | α=0,9 | ||
| 1991 | 6 | 6 | 6 | 6 | 6 | 6 |
| 1992 | 93 | 14,7 | 32,1 | 49,5 | 66,9 | 84,3 |
| 1993 | 693 | 82,53 | 230,37 | 371,25 | 505,17 | 632,13 |
| 1994 | 3554 | 429,677 | 1227,459 | 1962,625 | 2639,351 | 3261,813 |
| 1995 | 7350 | 1121,709 | 3064,221 | 4656,313 | 5936,805 | 6941,181 |
| 1996 | 9012 | 1910,738 | 4848,555 | 6834,156 | 8089,442 | 8804,918 |
| 1997 | 10751 | 2794,765 | 6619,288 | 8792,578 | 9952,532 | 10556,39 |
| 1998 | 11157,5 | 3631,038 | 7980,752 | 9975,039 | 10796,01 | 11097,39 |
| 1999 | 16838,5 | 4951,784 | 10638,08 | 13406,77 | 15025,75 | 16264,39 |
| 2000 | 21671,2 | 6623,726 | 13948,01 | 17538,98 | 19677,57 | 21130,52 |
| 2001 | 30485,2 | 9009,873 | 18909,17 | 24012,09 | 27242,91 | 29549,73 |
| 2002 | 39031,3 | 12012,02 | 24945,81 | 31521,7 | 35494,78 | 38083,14 |
| 2003 | 54365,1 | 16247,32 | 33771,6 | 42943,4 | 48704 | 52736,9 |
| 2004 | 66714,2 | 21294,01 | 43654,38 | 54828,8 | 61311,14 | 65316,47 |
Как видим, уже при ![]() =0,9 экспоненциальные средние практически воспроизводят сам динамический ряд и не характеризует тренд. Выбор константы сглаживания
=0,9 экспоненциальные средние практически воспроизводят сам динамический ряд и не характеризует тренд. Выбор константы сглаживания ![]() достаточно произволен. Обычно используются значения
достаточно произволен. Обычно используются значения ![]() в диапазоне от 0,1 до 0,5. При краткосрочных прогнозах чаще используется указанный диапазон значений
в диапазоне от 0,1 до 0,5. При краткосрочных прогнозах чаще используется указанный диапазон значений ![]() : при повышении
: при повышении ![]() увеличивается вес последних наблюдений. А для сглаживания случайных колебаний
увеличивается вес последних наблюдений. А для сглаживания случайных колебаний ![]() уменьшается. При увеличении срока прогноза более поздняя информация должна иметь несколько меньший вес, т.е. величина
уменьшается. При увеличении срока прогноза более поздняя информация должна иметь несколько меньший вес, т.е. величина![]() уменьшается.
уменьшается.
Вычисление прогноза по методу экспоненциальных средних
При использовании экспоненциальных средних в прогнозировании каждый новый прогноз основывается на предыдущем прогнозе:
![]() ,
,
где ![]() - прогноз для периода t;
- прогноз для периода t; ![]() - прогноз для периода (t-1);
- прогноз для периода (t-1); ![]() - сглаживающая константа;
- сглаживающая константа; ![]() - фактический уровень для периода (t-1).
- фактический уровень для периода (t-1).
Рассмотренный метод прогнозирования относится к классу адаптивных методов. Применительно к прогнозированию процесс адаптации состоит в том. Что при прогнозе на период t учитывается ошибка предыдущего прогноза, т.е. каждый новый прогноз ![]() получается в результате корректировки предыдущего прогноза с учетом его ошибки.
получается в результате корректировки предыдущего прогноза с учетом его ошибки.
Экспоненциальное сглаживание – широко распространенный метод прогнозирования из-за легкости вычисления. Для коротких временных рядов, которые часто встречаются в экономике, важным представляется выбор начальной оценки прогноза. Для этой цели могут быть использованы разные приемы: среднее значение нескольких первых периодов; субъективные оценки, полученные экспертным путем; первое фактическое значение уровня динамического ряда как прогноз для периода 2. Если принять последний подход, то при ![]() =0,3, получим прогнозные те же оценки, но сдвинутые на один год.
=0,3, получим прогнозные те же оценки, но сдвинутые на один год.
Рассмотренные экспоненциальные средние представляют собой средние первого порядка, т.е. средние, полученные при сглаживании уровней динамического ряда (первичное сглаживание). При прогнозировании могут использоваться экспоненциальные средние более высоких порядков, т.е. средние, полученные путем многократного сглаживания.
Похожие работы
... анализ, а также необходимо использование специальных методов прогнозирования временных рядов. 2 глава. Экономико-математические методы статистического анализа и прогнозирования доходов бюджета региона 2.1 Методы статистического анализа доходов бюджета региона Для количественной оценки динамики доходов бюджета региона применяются статистические показатели: абсолютные темпы роста и ...
... с методологией МОТ классифицируются как безработные. Прежде всего, дается информация об абсолютной численности безработных в стране и по регионам. Глава 3. Экономико–статистический анализ и прогнозирование безработицы 3.1. Экономический анализ безработицы Привычным явлением для некоторых категорий населения стала безработица. В 2005 году из общей численности трудовых ресурсов 252,4 тыс. ...
... найденное значение среднего темпа роста выступает в качестве коэффициента для составления прогноза на будущий срок. Высчитывается по формуле: (1.26) 2. Статистический показатель расчетов временных рядов (корреляция) Случайной величиной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин ...
... анализировать их тенденции и прогнозировать ситуацию в будущем. Все участники рынка ценных бумаг планируют свои операции только после тщательного анализа. Статистические методы прогнозирования развития рынка ценных бумаг основаны на построении фондовых индексов, расчете показателей дисперсии, вариации, ковариации, экстраполяции и интерполяции. Фондовые индексы являются самыми популярными во всём ...
0 комментариев