Навигация
Виды графов и операции над ними
28460
знаков
7
таблиц
5
изображений
3. Виды графов и операции над ними
3.1 Элементы графов
Для рассмотрения видов граф и операций над ними необходимо познакомиться с такими понятиями как подграфы, маршрут, цепь, цикл.
Граф G'(V', Е') называется подграфом графа G(V, Е) (обозначается G' Ì G), если V' Ì V и/или Е' Ì Е.
Если V' = V, то G ' называется остовным подграфом G.
Если V' Ì V & Е' Ì Е & (V' ¹ V Ú Е' ¹ Е), то граф G ' называется собственным подграфом графа G.
Подграф G'(V' , Е') называется правильным подграфом графа G(V,Е), если G ' содержит все возможные ребра G:
" и,v Î V' (и, v) Î Е Þ (и, v) Î Е'.
Правильный подграф G '(V ' , Е') графа G (V, Е) определяется подмножеством вер шин V '.
Маршрутом в графе называется чередующаяся последовательность вершин и ребер в которой любые два соседних элемента инцидентны.
v0, e1, v1, e2, v2,…,ek, vk,
Это определение подходит также для псевдо-, мульти- и орграфов. Для «обычного» графа достаточно указать только последовательность вершин или только последовательность ребер.
Если v0 = vk, то маршрут замкнут, иначе открыт. Если все ребра различны, то маршрут называется цепью. Если все вершины (а значит, и ребра) различны, то маршрут называется простой цепью. В цепи v0, e1, v1, e2, v2,…,ek, vk,
вершины v0 и vk,называются концами цепи. Говорят, что цепь с концами и и v соединяет вершины и и v. Цепь, соединяющая вершины и и v, обозначается (и, v). Очевидно, что если есть цепь, соединяющая вершины и и v, то есть и простая цепь, соединяющая эти вершины.
Замкнутая цепь называется циклом; замкнутая простая цепь называется простым циклом. Число циклов в графе G обозначается z(G). Граф без циклов называется ациклическим.
Элементы графа – любое чередование вершин и рёбер графа, в котором каждому ребру предшествует смежная ей вершина, называющаяся контуром графа.
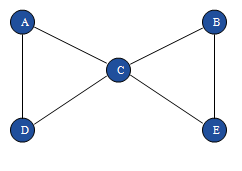
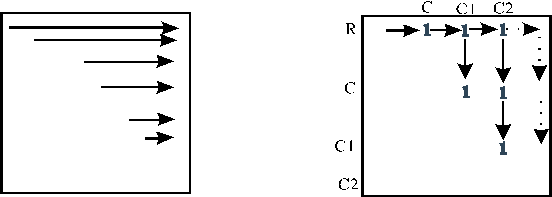
Рис 3.1 Маршруты, цепи, циклы
По рисунку 3.1 можно определить следующие утверждения:
1. A, C, A, D – маршрут, но не цепь;
2. A, C, E, B, C, D – цепь, но не простая цепь;
3. A, D, C, B, E, - простая цепь;
4. A, C, E, B, C, D, A – цикл, но не простой цикл;
5. A, C, D – простой цикл;
Цепь в ориентированном графе называется путём, а цикл – контуром.
3.2 Изоморфизм графов
Говорят, что два графа G1(V1 , Е1) и G2(V2 , Е2) изоморфны (обозначается G1 ~ G2), если существует биекция h: V1 ® V2, сохраняющая смежность:
e1 = ( u , v ) Î E1 Þ e2 = ( h( u ), h( v ) ) Î E2,
e2 = ( u , v ) Î E2 Þ e1 = ( h-1( u ), h-1( v ) ) Î E1
Изоморфизм графов есть отношение эквивалентности. Действительно, изомор физм обладает всеми необходимыми свойствами:
1. рефлексивность: G ~ G, где требуемая биекция суть тождественная функция;
2. симметричность: если G1 ~ G2 с биекцией h, то G2 ~ G1 с биекцией h-1;
3. транзитивность: если G1 ~ G2 с биекцией h, и G2 ~ G3 с биекцией g, тоG1 ~ G3 с биекцией g o h.
Графы рассматриваются с точностью до изоморфизма, то есть рассматриваются классы эквивалентности по отношению изоморфизма.
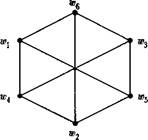Приведём примеры изоморфных графов рис. 3.2
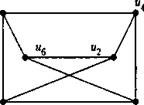
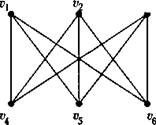
Рис. 3.2 Диаграммы изоморфных граф
Числовая характеристика, одинаковая для всех изоморфных графов, называется инвариантом графа. Так, р(G) и д(G) — инварианты графа С.
Не известно никакого набора инвариантов, определяющих граф с точностью до изоморфизма.
3.3 Тривиальные и полные графы
Граф, состоящий из одной вершины, называется тривиальным. Граф, состоящий из простого цикла с k вершинами, обозначается Сk.
Пример
С3 — треугольник.
Граф, в котором каждая пара вершин смежна, называется полным. Полный граф с р вершинами обозначается Кр, он имеет максимально возможное число ребер:
Полный подграф (некоторого графа) называется кликой (этого графа).
Похожие работы
... , "базовые" алгоритмы: поиск путей, определение компонент связности графа и т.д. 8. Ввод/вывод графов Одной из проблем при создании средств работы с помеченными графами является выбор внешнего файлового формата для хранения графов. До недавнего времени каждая программная система использовала свой собственный, уникальный формат, что приводило к сложностям при организации обмена данными. ...
... write(fileKlics,klika); end; end; end; {конец пеpебоpа возможных мест в стpоке} end; {конец пpохода по стpокам} close(fileklics); end; Выше представлена процедура нахождения клик в графе. Описание переменных: StolbecSravn: номер сравниваемого столбца. StringSravn: номер текущей строки. Num ,i1,i: счетчики. lenStolb: размер множества вершин клики. Stolbec: номер столбца первой ...
... . Вся процедура поиска представлена ниже (данная процедура используется также и для просмотра графа, и в псевдокоде, описанном ниже, отсутствуют операторы, которые не используются для поиска). 1 procedure WS (v); (*поиск в ширину в графе с началом в вершине v; переменные НОВЫЙ, ЗАПИСЬ — глобальные *) 2 begin 3 ОЧЕРЕДЬ := Æ; ОЧЕРЕДЬ <= v; НОВЫЙ [v] := ложь 4 while ОЧЕРЕДЬ &# ...
... файла из которого будет происходить ввод X – грав в последовательном представлении O(N,N1)=N2 N2 – количество вершин в графе X Текст программы. # include # include # include # include # include # include /////////////////////////////////////////////////////////////////////////////////////////////////////// struct Spisok //Связанное представление графа { int index; //Содержвтельная " ...
0 комментариев