Навигация
3.4 Двудольные графы
Двудольный граф (или биграф, или четный граф) — это граф G(V,Е), такой что множество V разбито на два непересекающихся множества V1 и V2 (V1 ÈV2 = V& V1 Ç V2) причем всякое ребро из Е инцидентно вершине из V1 и вершине из V2 (то есть соединяет вершину из V1 с вершиной из V2). Множества V1 и V2 называются долями двудольного графа. Если двудольный граф содержит все ребра, соединяющие множества V1 и V2, то он называется полным двудольным графом. Если | V1 | = m и | V1 | = п, то полный двудольный граф обозначается Km,n
3.5 Направленные орграфы и сети
Если в графе ориентировать все ребра, то получится орграф, который называется направленным. Направленный орграф, полученный из полного графа, называется турниром.
Название «турнир» имеет следующее происхождение. Рассмотрим спортивное соревнование для пар участников (или пар команд), где не предусматриваются ничьи. Пометим вершины орграфа участниками и проведем дуги от победителей к побежденным. В таком случае турнир в смысле теории графов — это как раз результат однокругового турнира в спортивном смысле.
Если в орграфе полустепень захода некоторой вершины равна нулю (то есть d+(v) = 0), то такая вершина называется источником, если же нулю равна полу степень исхода (то есть d-(v) = 0), то вершина называется стоком. Направлен ный орграф с одним источником и одним стоком называется сетью.
3.6 Операции над графами
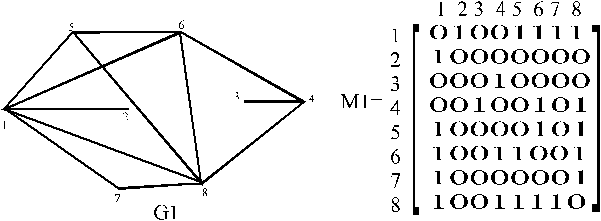
1. Дополнением графа G1(V1 , Е1) называется граф G(V2 , Е2) рис. 3.6.1, где
![]()


![]()
![]()
![]()
![]() V2 : = V1 & Е2 : = Ø Е1 : = {e Î V1 ´ V1 ê e Ï Е1}
V2 : = V1 & Е2 : = Ø Е1 : = {e Î V1 ´ V1 ê e Ï Е1}![]()
![]()
![]()
![]()
![]()
![]()
![]()
G1ØG
Рис 3.6.1 Дополнение
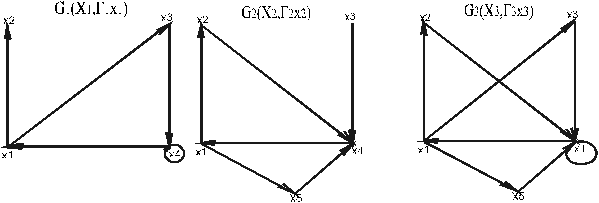
Объединением графов G1(V1 , Е1) и G2(V2 , Е2) (обозначение - G1 È G2, при условии V1 ÇV1 = Æ, Е1 ÇЕ2 = Æ) называется граф G(V,E), рис. 3.6.3
V : = V2 È V1 & Е : = Е1 ÇЕ2
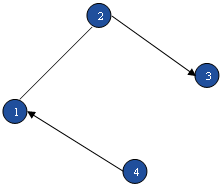
Рис. 3.6.3 Объединение графов
2. Соединением графов G1(V1 , Е1) и G2(V2 , Е2)(обозначение - G1(V1 , Е1) + G2(V2 , Е2), при условии V1 Ç V2 называется граф G(V,E), где
V : = V1 Ç V2 & E : = Е1 È Е2 È {e = (v1, v2) êv1 Î V1 & v2 Î V2}
3. Удаление вершины v из графа G1(V1 , Е1) (обозначение - G1(V1 , Е1) – v, при условии vÎV1) даёт граф G2(V2 , Е2), где
V2 : = V1 \ {v} & E2 : = E1 \ {e = (v1 , v2) ê v1 = v Ú v2 = v}
4. Удаление ребра e из графа G1(V1 , Е1)(обозначение - G1(V1 , Е1) – e, при условии e Î E1) даёт граф G2(V2 , Е2), где
V2 : = V1 & E2 : = E1 \ {e}
5. Добавление вершины v в граф G1(V1 , Е1) (обозначение - G1(V1 , Е1) + v, при условии v Ï V1) даёт граф G2(V2 , Е2), где
V2 : = V1 È {v} & E2 : = E1
6. Добавление ребра e в граф G1(V1 , Е1) (обозначение - G1(V1 , Е1) + v, при условии e Ï E1) даёт граф G2(V2 , Е2), где
V2 : = V1 & E2 : = E1 È {e}
7. Стягивание подграфа А графа G1(V1 , Е1) (обозначение - G1(V1 , Е1) / А, при условии А Ì V1) даёт граф G2(V2 , Е2), где
V2 : = (V1 \ A) È {v} &
E2 : = E1 \ {e = (u,w) êu Î A Ú w Î A} È {e = (u,v) êu Î Г(А) \ А}
Похожие работы
... , "базовые" алгоритмы: поиск путей, определение компонент связности графа и т.д. 8. Ввод/вывод графов Одной из проблем при создании средств работы с помеченными графами является выбор внешнего файлового формата для хранения графов. До недавнего времени каждая программная система использовала свой собственный, уникальный формат, что приводило к сложностям при организации обмена данными. ...
... write(fileKlics,klika); end; end; end; {конец пеpебоpа возможных мест в стpоке} end; {конец пpохода по стpокам} close(fileklics); end; Выше представлена процедура нахождения клик в графе. Описание переменных: StolbecSravn: номер сравниваемого столбца. StringSravn: номер текущей строки. Num ,i1,i: счетчики. lenStolb: размер множества вершин клики. Stolbec: номер столбца первой ...
... . Вся процедура поиска представлена ниже (данная процедура используется также и для просмотра графа, и в псевдокоде, описанном ниже, отсутствуют операторы, которые не используются для поиска). 1 procedure WS (v); (*поиск в ширину в графе с началом в вершине v; переменные НОВЫЙ, ЗАПИСЬ — глобальные *) 2 begin 3 ОЧЕРЕДЬ := Æ; ОЧЕРЕДЬ <= v; НОВЫЙ [v] := ложь 4 while ОЧЕРЕДЬ &# ...
... файла из которого будет происходить ввод X – грав в последовательном представлении O(N,N1)=N2 N2 – количество вершин в графе X Текст программы. # include # include # include # include # include # include /////////////////////////////////////////////////////////////////////////////////////////////////////// struct Spisok //Связанное представление графа { int index; //Содержвтельная " ...
0 комментариев