Навигация
4. Решение задачи
4.1 Математическое решение задачи
Условие задачи:
Три предприятия данного экономического района могут производить однородную продукцию, в количествах соответственно равных А1, А2 и А3 единиц. Эта продукция должна быть поставлена 5-и потребителям в количествах, соответственно равных В1, В2, В3, В4 и В5 единиц. Затраты связанные с производством и доставкой продукции, задаются матрицей С.
А1=180; А2=350; А3=20
В1=110; В2=90; В3=120; В4=80; В5=150
Таблица 7
Индексы матрицы
| В1 | В2 | В3 | В4 | В5 | |
| А1 | 7 | 12 | 4 | 6 | 5 |
| А2 | 1 | 8 | 6 | 5 | 3 |
| А3 | 6 | 13 | 8 | 7 | 4 |
Таблица 8
Первоначальное заполнение ячеек
| 7 | 12 | 4 | 6 | 5 | 180 | |||||
| 110 | 70 | |||||||||
| 1 | 8 | 6 | 5 | 3 | 350 | |||||
| 20 | 120 | 80 | 130 | |||||||
| 6 | 13 | 8 | 7 | 4 | 20 | |||||
| 20 | ||||||||||
| 110 | 90 | 120 | 80 | 150 | ||||||
Найдем целевую функцию:
Z=110*7+70*12+20*8+120*6+80*5+130*3+20*4=3360
Таблица 9
Первое оценивание ячеек
| 1-С | 1-D | 1-E | 2-A | |||||||
| +4 | -12 | +6 | -12 | +5 | -12 | +1 | -7 | |||
| +8 | -6 | +8 | -5 | +8 | -3 | +12 | -8 | |||
| -6 | -3 | -2 | 0 | |||||||
| 3-A | 3-B | 3-C | 3-D | |||||||
| +6 | -7 | +13 | -8 | +8 | -6 | +7 | -5 | |||
| +12 | -8 | +3 | -4 | +3 | -4 | +3 | -4 | |||
| +6 | -5 | +4 | +1 | +1 | ||||||
| +3 | -4 | |||||||||
| +3 | ||||||||||
Таблица 10
Редактирование таблицы от оцененной ячейки
| 7 | 12 | 4 | 6 | 5 | 180 | |||||
| 110 | 70 | |||||||||
| 1 | 8 | 6 | 5 | 3 | 350 | |||||
| 90 | 50 | 80 | 130 | |||||||
| 6 | 13 | 8 | 7 | 4 | 20 | |||||
| 20 | ||||||||||
| 110 | 90 | 120 | 80 | 150 | ||||||
Повторим для результата нахождение целевой функции с новыми параметрами:
Z=110*7+70*4+90*8+50*6+80*5+130*3+20*4=2940
Таблица 11
Второй шаг оценки ячеек
| 1-B | 1-D | 1-E | 2-A | |||||||
| +12 | -4 | +6 | -4 | +5 | -4 | +1 | -7 | |||
| +6 | -8 | +6 | -5 | +6 | -3 | +4 | -6 | |||
| 6 | 3 | 4 | -8 | |||||||
| 3-A | 3-B | 3-C | 3-D | |||||||
| +6 | -7 | +13 | -8 | +8 | -6 | +7 | -5 | |||
| +4 | -6 | +3 | -4 | +3 | -4 | +3 | -4 | |||
| +3 | -4 | +4 | +1 | +1 | ||||||
| -4 | ||||||||||
Таблица 12
Шаг третий
| 7 | 12 | 4 | 6 | 5 | 180 | |||||
| 60 | 120 | |||||||||
| 1 | 8 | 6 | 5 | 3 | 350 | |||||
| 50 | 90 | 80 | 130 | |||||||
| 6 | 13 | 8 | 7 | 4 | 20 | |||||
| 20 | ||||||||||
| 110 | 90 | 120 | 80 | 150 | ||||||
Находим целевую функцию
Z=60*7+120*4+50+90*8+80*5+130*3+20*4=2540
Таблица 13
Оценивание ячеек на шаге 3
| 1-B | 1-D | 1-E | 2-A | |||||||
| +12 | -7 | +6 | -7 | +5 | -7 | +6 | -1 | |||
| +1 | -8 | +1 | -5 | +1 | -3 | +7 | -4 | |||
| -2 | -5 | -4 | 8 | |||||||
| 3-C | 3-A | 3-B | 3-D | |||||||
| +8 | -4 | +6 | -1 | +13 | -8 | +7 | -5 | |||
| +7 | -1 | +3 | -4 | +3 | -4 | +3 | -4 | |||
| +3 | -4 | +4 | +4 | +1 | ||||||
| +7 | ||||||||||
Таблица 14
Четвертый шаг
| 7 | 12 | 4 | 6 | 5 | 180 | |||||
| 120 | 60 | |||||||||
| 1 | 8 | 6 | 5 | 3 | 350 | |||||
| 110 | 90 | 20 | 130 | |||||||
| 6 | 13 | 8 | 7 | 4 | 20 | |||||
| 20 | ||||||||||
| 110 | 90 | 120 | 80 | 150 | ||||||
Z=120*4+60*6+110+90*8+20*5+130*3+20*4=2240
Таблица 15
Оценивание ячеек на 4 шаге
| 1-A | 1-B | 1-E | 2-C | |||||||
| +7 | -6 | +12 | -8 | +5 | -6 | +6 | -5 | |||
| +5 | -1 | +5 | -6 | +5 | -3 | +6 | -4 | |||
| 5 | 3 | 1 | 3 | |||||||
| 3-C | 3-A | 3-B | 3-D | |||||||
| +8 | -4 | +6 | -1 | +13 | -8 | +7 | -5 | |||
| +6 | -5 | +3 | -4 | +3 | -4 | +3 | -4 | |||
| +3 | -4 | +4 | +4 | +1 | ||||||
| +4 | ||||||||||
Похожие работы
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... получение которого связано с большим объемом вычислительных работ. Обычно рассмотренный метод используется при вычислениях с помощью ЭВМ. Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом. Для определения оптимального плана транспортной задачи можно использовать изложенные выше методы. Однако ввиду исключительной практической ...
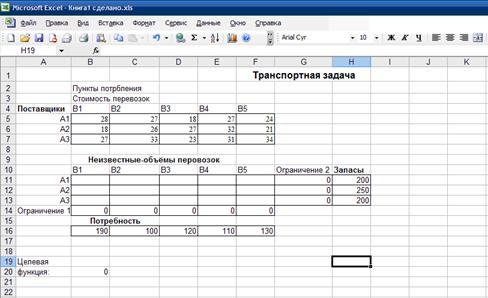
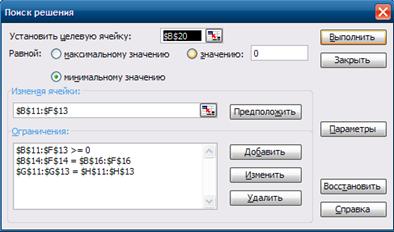
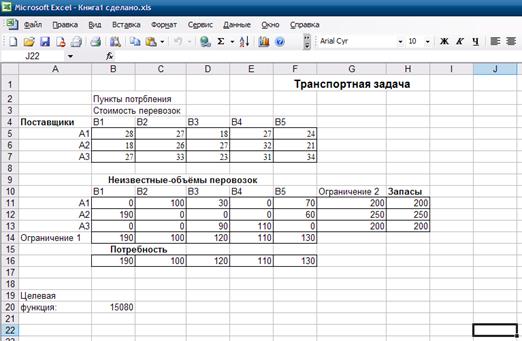
... F = 27*100 + 30*30 + 24*70 + 18*190 + 21*60 + 23*120 + 31*80 = 15110 Результат: Затраты на распределение товаров между магазинами найденные методом наименьшей стоимости составят 15110 рублей. 2.6 Применение возможностей электронных таблиц при решении транспортной задачи Для решения транспортной задачи также можно применять электронные таблицы (Microsoft Office Excel ). Для решения ...

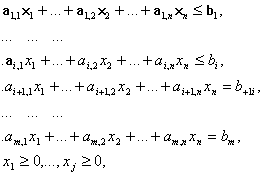
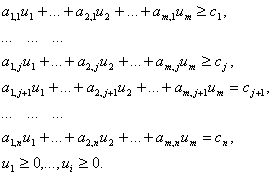







0 комментариев