Навигация
Руководство пользователя
4.4 Руководство пользователя
Пуск
Запуск из среды Pascal производится нажатием клавиш Ctrl+F9, а из Norton Commander нажатием клавиши Enter на файле Inform.exe.
Ввод данных
Ввод данных производится только с цифровой клавиатуры. Цифры от 0 до 9.
Просмотр результатов.
После ввода цифры (нужного пункта в меню) выводится требуемый результат и после просмотра результата нужно нажать Enter. Затем вновь появится меню на экране.
Выход из программы
Выход из программы в среде Pascal и после запуска PTransport.exe файла производится 0-ым пунктом меню.
5. Анализ результатов
При решении задачи были получены результаты удовлетворяющие условию:
Решая задачу математически, получили значения:
| 7 | 12 | 4 | 6 | 5 | 180 | |||||
| 120 | 60 | |||||||||
| 1 | 8 | 6 | 5 | 3 | 350 | |||||
| 110 | 90 | 20 | 130 | |||||||
| 6 | 13 | 8 | 7 | 4 | 20 | |||||
| 20 | ||||||||||
| 110 | 90 | 120 | 80 | 150 | ||||||
Z=120*4+60*6+110+90*8+20*5+130*3+20*4=2240
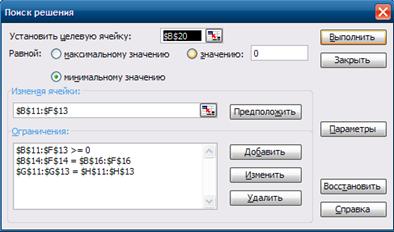
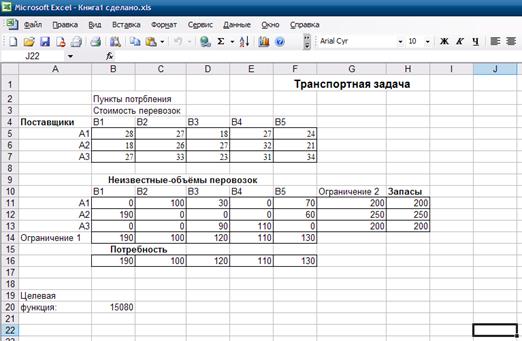
При решении задачи в программе Excel получили значения:
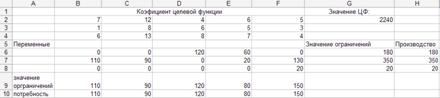
В программе, созданной для решения задачи, получили тот же результат.
Соответственно можно сделать вывод, что задача была решена правильно.
Заключение
В курсовой работе изложены основные подходы и методы решения транспортной задачи, являющейся одной из наиболее распространенных задач линейного программирования. Решение данной задачи позволяет разработать наиболее рациональные пути и способы транспортирования товаров, устранить чрезмерно дальние, встречные, повторные перевозки. Все это сокращает время продвижения товаров, уменьшает затраты предприятий и фирм, связанные с осуществлением процессов снабжения сырьем, материалами, топливом, оборудованием и т.д.
В данной курсовой работе поставлена задача: минимизировать затраты на транспортировку продукции потребителям. При выполнении курсовой работы были использованы знания по предметам: «Математические методы», «Пакеты прикладных программ». Решение было проведено с помощью пакетов прикладных программ Microsoft Excel и Microsoft Word. Результаты ручного просчёта сравнивались с результатами, полученными в Microsoft Excel.
Курсовая работа выполнена в полном объёме в соответствии с требованиями ГОСТ.
Список использованной литературы:
1. Е.Г. Гольштейн, Д.Б. Юдин «Задачи линейного программирования транспортного типа», Москва, 1993.
2. И.Л. Акулич, В.Ф. Стрельчонок «Математические методы и компьютерные технологии решения оптимизационных задач», Рига, 2000.
3. www.fmi.asf.ru
4. Кузнецов А.В., Сакович В.А., Холод Н.И. ”Высшая математика. Математическое программирование”, Минск, Вышейшая школа, 2001г.
5. Боборыкин В.А. Математические методы решения транспортных задач. Л.: СЗПИ, 1986
6. Геронимус Б.А. Экономико-математические методы в планировании наавтомобильном транспорте. М.: Транспорт, 1982
7. Кузнецов Ю.Н., Кузубов В.И., Волощснко А. Б. Математическоепрограммирование. М.: Высшая школа, 1980
8. Красс М.С., Чупрынов Б.П. ”Основы математики и ее приложения в экономическом образовании”, Издательство “Дело”, Москва 2001г.
9. В.И. Ермаков “Общий курс высшей математики для экономистов”, Москва, Инфра-М, 2000г.
10. Еремин И.И., Астафьев Н.Н. Введение в теорию линейного и выпуклого программирования М.; Наука, 1976г.
11. Карманов В.Г. Математическое программирование. – М.; Наука, 1986г.
12. Моисеев Н.Н., Иванов Ю.П., Столярова Е.М. Методы оптимизации. – М.; Наука, 1978г.
Похожие работы
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... получение которого связано с большим объемом вычислительных работ. Обычно рассмотренный метод используется при вычислениях с помощью ЭВМ. Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом. Для определения оптимального плана транспортной задачи можно использовать изложенные выше методы. Однако ввиду исключительной практической ...
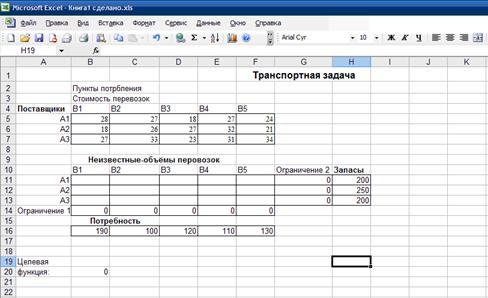
... F = 27*100 + 30*30 + 24*70 + 18*190 + 21*60 + 23*120 + 31*80 = 15110 Результат: Затраты на распределение товаров между магазинами найденные методом наименьшей стоимости составят 15110 рублей. 2.6 Применение возможностей электронных таблиц при решении транспортной задачи Для решения транспортной задачи также можно применять электронные таблицы (Microsoft Office Excel ). Для решения ...








0 комментариев