Навигация
Содержательная постановка задачи
2. Содержательная постановка задачи
Частным случаем задачи линейного программирования является транспортная задача. Проблема транспортировки включает поиск низко затратных схем распределения товарных запасов от многих источников до многих мест назначения.
Отгрузочными пунктами (поставщиками) являются фабрики, склады, отделы, из которых отправляются товары. Местом назначения также могут быть фабрики, склады, отделы, которые получают товары.
Информация необходимая для использования модели включает следущее:
- список отправных пунктов и пропускная способность каждого (количество поставок за определенный период);
- список мест назначения и их показатели спроса;
- стоимость транспортировки единицы продукции от каждого отправленного пункта до каждого места назначения. Эта информация сводится в транспортную таблицу.
3. Математическая постановка задачи
Пусть Xij - количество груза перевозимого из пункта i в пункт j.
А1=40; А2=50; В1=20; В2=30; В3=40;
![]()
![]() 3 5 7
3 5 7
С = 4 6 10
Таблица 5
Начальные параметры
| B1 | B2 | B3 | |||||
| A1 | 3 | 5 | 7 | ||||
| 40 | |||||||
| A2 | 4 | 6 | 10 | 50 | |||
| 20 | 30 | 40 | |||||
Целевая функция имеет вид:
![]()
Ограничение по запасам:
![]()
Х11 + Х12 + Х13 <= 40
Х21 + Х22 + Х23 <= 50
Xij>=0
Ограничение по спросу:
Х11 + Х21 <= 20
Х12 + Х22 <= 30
Х13 + Х23 <= 40
Этапы решения транспортной задачи:
1) Получение начального решения
2) Проверка решений на оптимальность
3) Усовершенствование несовершенных решений
Интуитивный подход.
Проверка на оптимальность и пересмотр несовершенных решений предусматривает анализ каждой пустой ячейки. Это выполняется так: одна единица перемещается в пустую ячейку и рассматривается влияние этого перемещения на стоимость. Если стоимость увеличилась, то это значит, что использование ячейки увеличило бы общие затраты. Если стоимость осталась не изменой, это значит альтернативный план с той же общей стоимостью. Если анализ показывает уменьшение – это значит возможно лучшее решение.
Таблица 6
Заполнение ячеек
| B1 | B2 | B3 | |||||
| A1 | 3 | 5 | 7 | ||||
| 20 | 20 | 40 | |||||
| A2 | 4 | 6 | 10 | 50 | |||
| 10 | 40 | ||||||
| 20 | 30 | 40 | |||||
Целевая функция:
Z=3*20+5*20+6*10+10*40=60+100+60+400=620
Похожие работы
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... получение которого связано с большим объемом вычислительных работ. Обычно рассмотренный метод используется при вычислениях с помощью ЭВМ. Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом. Для определения оптимального плана транспортной задачи можно использовать изложенные выше методы. Однако ввиду исключительной практической ...
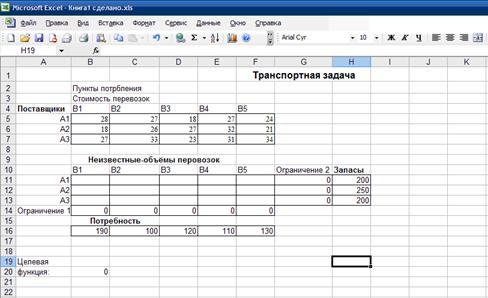
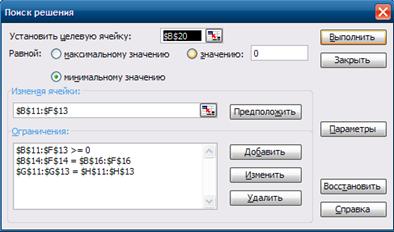
... F = 27*100 + 30*30 + 24*70 + 18*190 + 21*60 + 23*120 + 31*80 = 15110 Результат: Затраты на распределение товаров между магазинами найденные методом наименьшей стоимости составят 15110 рублей. 2.6 Применение возможностей электронных таблиц при решении транспортной задачи Для решения транспортной задачи также можно применять электронные таблицы (Microsoft Office Excel ). Для решения ...

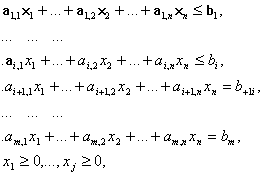
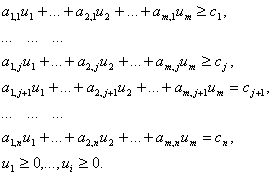







0 комментариев