Навигация
Вершинами A подграфа G(A,UA) является некоторое подмножество вершин графа G(X,U);
1. Вершинами A подграфа G(A,UA) является некоторое подмножество вершин графа G(X,U);
2. Отображением каждой вершины подграфа является пересечение отображения той же вершины в графе G(X,U) со всем подмножеством вершин A подграфа G(A,UA).
Частичным графом для графа G(X,U) называется граф G(X,U), в котором содержатся все вершины и некоторое подмножество дуг исходного графа.
Частичный подграф - это частичный граф от подграфа.
Фактором графа G(X,U) называется частичный граф G(X,U), в котором каждая вершина обладает полустепенями исхода и захода, равными единице, имеются одна заходящая и одна исходящая дуги.
Базисным графом называется ориентированный частичный граф, образованный из исходного удалением петель и замыкающих дуг.
Связность графаВ общем случае граф может быть представлен несколькими отдельными графами, не имеющими общих дуг. Тогда граф G(X,U) называется несвязным, а каждый из составляющих его графов G1 , G2 ,...Gn - компонентами связности. Граф называется связным, когда каждую его вершину можно соединить с любой другой его вершиной некоторой цепью.
Операции над графами1. Объединение графов
G3(X3,Гх3) = G1(X1,Г1х1) È G2(X2,Г2х2), где X3=X1ÈX2, а Гx3=Г1x1ÈГ2x2
Пример (Рис 1.1).
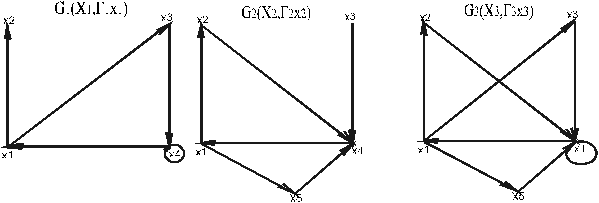 Рис 1.1
Рис 1.1
2. Пересечение графов
G3(X3,Гх3) = G1(X1,Г1х1) ÇG2(X2,Г2х2), где X3=X1Ç X2, а Гx3=Г1x1ÇГ2x2
Пример (рис 1.2).
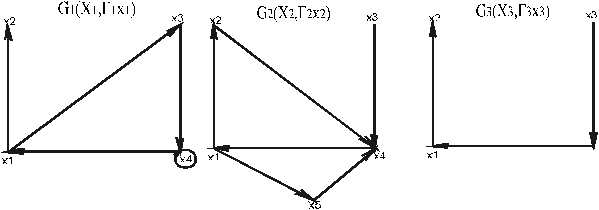 Рис 1.2
Рис 1.2
4. Прямое (декартово) произведение графов.
Прямым произведением множеств Х{x1.......xn} и Y называется множество Z, элементами которого являются всевозможные пары вида xi , yj , где xiÎX, yjÎY. Обозначают: Z=X x Y.
G3(X3,Гх3) = G1(X1,Г1х1) Ç G2(X2,Г2х2), где X3=X1ÇX2, а Гx3=Г1х1ÇГ2х2
Пример. (рис 2.3)
G1(X,Гх)=G1(X1,Гх1) G2(Y,Гy)= G2(X2,Гх2)
X={x1 x2 x3 } Y={y1 y2}
Гх1=0 Гу1={y1 y1}
Гх2={x1 x3} Гу2={y1}
Гх3=0
Z=X x Y={x1 y1, x1y2, x2y1, x2y2, x3y1, x3y2}
Z={z1 z2 z3 z4 z5 z6}
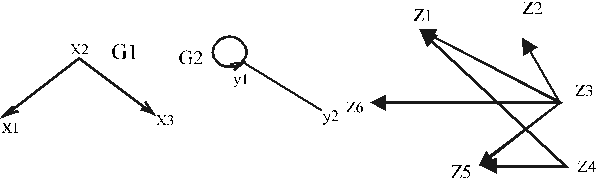
Рис 2.3
7. Расширение графа.
Расширение графа - это превращение, линии, соединяющей любые две вершины графа в элементарный путь введением новых промежуточных вершин на этой линии.
8. Сжатие графа.
Сжатие графа - это превращение элементарного пути, соединяющего две любые вершины графа, в линию.
9. Стягивание графа.
Если граф содержит вершины Х1 и Y1 , то операцией стягивания называется исключение всех дуг между вершинами Х1 и Y1 и превращение всех вершин в одну общую вершину Х.
Некоторые числа теории графовПусть существует мультиграф с b вершинами, p ребрами, и R компонентами связности, тогда цикломатическое число мультиграфа определяется равенством:
V= p-b+R
Матрицы для графовМатрицей смежности графа G(X,Гх), содержащего n вершин называется квадратная бинарная матрица А(G) n x n , c нулями на диагонали. Число единиц в строке равно степени соответствующей вершины.
Матрицей инциденций ориентированного графа G(X,U) называется прямоугольная матрица порядка [m x n] n - мощность множества Х, m - мощность множества U. Каждый элемент которой определяется следующим образом:
![]() 1, если хi - начало дуги Uj
1, если хi - начало дуги Uj
aij = -1, если хi - конец дуги Uj
0, если хi - не инцидентна дуге Uj
Пример.
Построим матрицы смежности (М1) и инциденций (М2) для графа G(X,U) (рис 2.1).
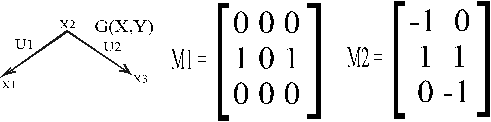
Рис 2.1
Дополнительная матрица графа G(X,U) представляет собой квадратную матрицу А1 , которая получается из матрицы смежности этого графа путем замены всех нулей единицами и наоборот.
Деревья и прадеревья
Деревом называется неориентированный связный граф с числом вершин не менее двух, не содержащий петель и циклов. Вершины, инцидентные только одной дуге дерева, называются висячими.
Прадрево - ориентированное дерево.
Корень прадерева - вершина у которой Р+(х)=0.
Глава 2. Максимальные полные подграфы (клики)Максимальный полный подграф (клика) графа G есть порожденный подграф, построенный на подмножестве S вершин графа и являющийся полным и максимальным в том смысле, что любой другой подграф графа G, построенный на множестве вершин H, содержащих S, не является полным. Следовательно, в клике все вершины попарно смежны. Возможно также определить кликовое число графа (известное также как густота или плотность) - это максимальное число вершин в кликах данного графа.
Часть 2. Практическая реализация курсового проектаЗадание
В неориентированном графе заданном матрицей смежностей выделить клики. Написать программу выполняющую это действие.
Решение
Мой алгоритм нахождения клик в графе
Пусть задан неориентированный граф G1 матрицей смежностей M1 (рис 3.1)
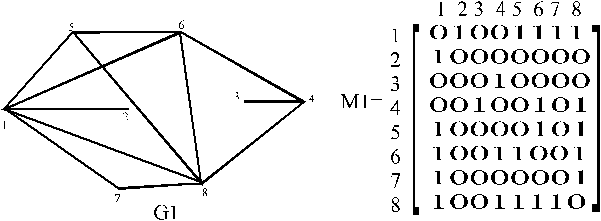 Рис 3.1
Рис 3.1
Замечаем следующее:
1) Что матрица М1 симметрична относительно главной диагонали, так как вершины неориентированного графа попарно смежны.
2) Если выделить клику из данного графа и представить ее в виде матрицы смежностей то получим матрицу вида:
![]() 01111 Тоесть тоже симметричную относительно главной диагонали и в верхнем
01111 Тоесть тоже симметричную относительно главной диагонали и в верхнем
10111 и нижнем треугольниках ее будут находится 1 а на главной диагонали 0,
11011 так получается потому, что все вершины попарно смежны (см опред.
11101 клики.
На основе наблюдений приходим к выводу, что для отыскания клик в неориентированном графе нужно выделить в исходной матрице смежностей подматрицы указанного выше вида, множества вершин образующие эти матрицы и будут вершинами клики. Но по определению клики нам подойдут не все такие множества, а лишь оригинальные не содержащих в себе других множеств вершин. Так что вторая задача будет сводится к выделению из полученных множеств оригинальных, не содержащих в себе других подмножестве. То что исходная матрица смежностей симметрична относительно главной диагонали позволят нам осуществлять поиск подматриц только в ее верхнем или нижнем треугольнике.
Шаг 1.
Идем по матрице как показано на рисунке 3.2 а и ищем первую попавшуюся единичку (рис 3.2 б) запоминаем ее координаты (R,C) .
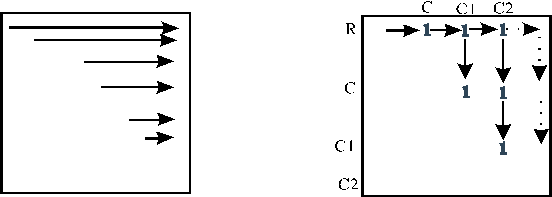
Шаг 2.
Ищем следующую 1 по адресу (R,C1)
Шаг 3.
Начинаем спускаться по столбцу (С1) в поисках 1 , причем ищем ее по адресу (С,С1), так как в исходной матрице столбцы попарно смежных вершин не обязательно соседствуют. Запоминаем строку каждой найденной таким образом 1 для поиска в следующих столбцах. Увеличиваем длину множества вершин на 1.
Количество повторений шага 3 равно текущему размеру множества вершин.
Если по указанному адресу мы не встречаем 1 то значит данный столбец не образует подматрицу смежностей клики - пропускаем его. Начинаем Шаг 2.
Если размер множества вершин образующих клику больше 2 то запоминаем это множество.
Так до конца строки.
Повторяем Шаг 1 для всех 1 в строке.
Таким образом проходим всю матрицу. На выходе получаем несколько множеств вершин, отбираем среди них только оригинальные, не содержащие в себе других подмножеств.
Отобранные подмножества и есть клики заданного графа.
Программная реализация
procedure MakeKliks;
var StolbecSravn,StringSravn,Num,size,i1,i,lenStolb,
Stolbec,RetStolb:byte;
Kstring:klik;
f1:file of byte;
klika:tKlik;
begin
assign(FileKlics,'klics.ots');
rewrite(fileKlics);
assign(f1,'matrica.ots');
reset(f1);
read(f1,size);
for I:=1 to size do
begin
for stolbecsravn:=1 to size do
begin
read(f1,smezh[i,stolbecsravn]);
end;
end;
for i:=1 to size do
begin {начало пpохода по стpокам}
KString[1]:=i;
for stolbec:=i+1 to size do
begin {пеpебиpаем в стpоке все возможные места начала клики}
If Smezh[i,stolbec]=1 then
begin
lenStolb:=1;
for StolbecSravn:=Stolbec to size do
begin {с найденного места пpовеpяем все возможные ваpианты}
StringSravn:=i;
Num:=1;
while (Smezh[KString[num],StolbecSravn]=1)and(num<=LenStolb) do
begin
StringSravn:=KString[num];
num:=num+1;
end;
If num-1=LenStolb then
begin
lenStolb:=lenStolb+1;
Kstring[lenStolb]:=StolbecSravn;
end;
end; {конец пpовеpки ваpиантов}
if lenstolb>2 then
begin
klika.lenmass:=lenstolb;
for i1:=1 to lenstolb do
klika.Klikmass[i1]:=Kstring[i1];
write(fileKlics,klika);
end;
end;
end; {конец пеpебоpа возможных мест в стpоке}
end; {конец пpохода по стpокам}
close(fileklics);
end;
Выше представлена процедура нахождения клик в графе.
Описание переменных:
StolbecSravn: номер сравниваемого столбца.
StringSravn: номер текущей строки.
Num ,i1,i: счетчики.
lenStolb: размер множества вершин клики.
Stolbec: номер столбца первой единицы в текущем цикле сравнения.
size: размер матрицы смежностей.
Kstring: вектор хранящий координаты строк для сравнения. По выходе из цикла сравнения этот массив представляет собой множество вершин найденной клики.
Smezh: Матрица смежностей;
Найденные клики сохраняются в файле klics.ots. Потом из него удаляются все клики несоответствующие вышеприведенным условиям. На выходе получаем файл клик задаваемого графа.
Пример
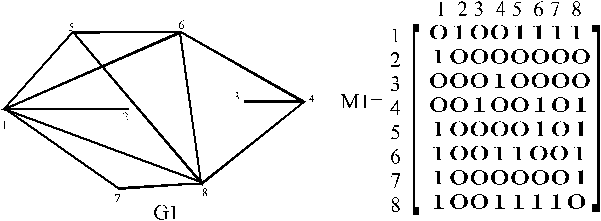
Задаем граф G1 его матрицей смежности М1.
Берем первую строку, находим первую единичку по адресу (1,2).
Запоминаем адрес первой 1 (1,2). Ищем следующую 1 в первой строке. Она находится по адресу (1,5). Проверяем адрес (2,5) на 1. Там ее нет. Пропускаем 5-й столбец. Находим следующую 1 в 6 столбце. Проверяем адрес (2,6) на 1. Там ее нет. так до конца строки. Убеждаемся что в данном цикле сравнений матрица смежностей получаемой клики имеет размерность два. Что означает наличие в клике двух вершин - простейшее сочетание - оно не рассматривается в моей программе. Мы записываем в файл клик клики не меньше третьего порядка.
Выбираем в первой строке следующую 1. Она находится по адресу (1,5) запоминаем этот адрес в массиве строк. Ищем следующую 1 в первой строке. Она находится по адресу (1,6). Спускаемся по 6 столбцу, проверяем адрес (5,6) на 1. Она там есть. Количество найденных 1 в 6 столбце =размеру массива содержащего множества. Тогда увеличиваем длину этого массива на 1 и записываем туда 6. Получаем в массиве [1,5,6]. И т.д.
В итоге получим клики с номерами вершин: 1 5 6 8; 6 4 8; 1 7 8.
Матрица смежностей клики 1568.
1 5 6 8
10 1 1 1
51 0 1 1
61 1 0 1
81 1 1 0
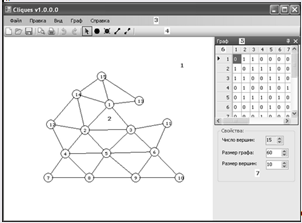
Работа с программой
Программа позволяет найти клики в неориентированном графе размером не более 10 вершин. Граф вводится в ЭВМ матрицей смежностей. Данную матрицу можно взять из вшитого в программу файла. Программа позволяет удобно редактировать заданную матрицу, для выхода из редактирования нажать Esc. Результат работы программы выводится в виде таблицы по количеству вершин клик и номеров самих вершин составляющих клики.
Программа реализована на языке программирования Turbo Pascal 7.0.
ЗаключениеПрограммная реализация на ЭВМ поиска максимальных полных подграфов(клик) значительно облегчает работу с графами, как представлением каких либо систем, в смысле исследования этих систем. Мой алгоритм позволяет найти клики в графе любой размерности, но для наглядности я реализовал алгоритм только для графов чья мощность не превышает 10. Так же мой алгоритм за добавлением одного условия будет искать клики и в ориентированном графе. Но моей целью не было создание профессиональной часто используемой программы, а скорее я хотел показать возможность решения данной задачи на ЭВМ.
Список литературыКовалева Л.Ф. “Математическая логика и теория графов” МЭСИ 1977
А Кристофидес “Теория графов. Алгоритмический под
Похожие работы
... не соединенными ребрами вершинами – на графе из двух вершин, соединенных ребром – на сложном графе Стратегия тестирования Сперва, с помощью определения понятия "клика", были найдены клики данного графа, после чего результаты сравнивались с результатом работы программы. 1. Тестирование на пустом графе. Теоретические расчеты: поскольку граф пуст (множество его вершин есть пустое множество) ...
... и алгоритмы на основе методов целочисленного линейного программирования. К приближенный алгоритмам раскраски относятся алгоритмы, основанные на упорядочивании множества вершин графов , последовательном удалении из графа вершин, имеющих максимальную степень и на анализе подмножеств смежности вершин. 2.1 Точные алгоритмы Алгоритм, использующий метод Магу - Вейссмана 1. Для графа G (Х,U) ...
... . 4.1 Требования к представлению графов Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Представление выбирается, исходя из потребностей конкретной задачи. Далее приведены четыре наиболее часто используемых представления с указанием характеристики п(р, q) — объема памяти для ...
... Gg:=Qp*A[i]; end Закончим трассировку примера. 2 [5] [2] [] 1 [5] [1,2,3] [] Выход в основную программу. Мы нашли все максимальные независимые множества. 3. Доминирующие множества Для графа G=(V, E) доминирующее множество вершин есть множество вершин SÌV, такое, что для каждой вершины j, не входящей в S, существует ребро, идущее из некоторой вершины ...
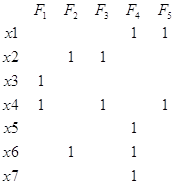

0 комментариев