Навигация
Статистичні ряди розподілу
5. Статистичні ряди розподілу
Наслідки зведення і групування статистичних даних можна представити у вигляді статистичних рядів розподілу.
Статистичний ряд розподілу – це упорядковане розміщення одиниць досліджуваної сукупності на групи за групувальною ознакою. Вони характеризують склад (структуру) досліджуваного явища, дають змогу встановити однорідність сукупності, а також закономірності її розвитку.
Ряди розподілу можуть бути атрибутивними і варіаційними.
Атрибутивні ряди розподілу – це такі, які побудовані за якісною ознакою; варіаційні – за кількісною ознакою. Кожний ряд розподілу складається із двох елементів: перший – це перелік груп, другий – їх чисельність у ряду розподілу. Прикладом атрибутивного ряду розподілу може бути розподіл населення або осіб, які вчинили злочин, за статтю (чоловіки та жінки), за місцем проживання (міське та сільське), за рівнем освіти, характером заняття; розподіл усіх злочинів за статтями КК; розподіл цивільних справ за категоріями; розподіл позивачів та відповідачів тощо.
При побудові атрибутивних рядів розподілу утворюють стільки груп, скільки різновидів атрибутивної ознаки має досліджувана сукупність. Ряд розподілу прийнято зображувати у вигляді таблиць. Для наочності наведемо атрибутивний ряд розподілу (табл. 1).
Таблиця 1. Розподіл засуджених за основними видами покарань, які були призначені судами України
| Вид покарання | 2008 р. | 2009 р. | ||
| кількість | % | кількість | % | |
| Позбавлення волі | 70308 | 34,9 | 61013 | 31,4 |
| Конфіскація майна | 33907 | 16,8 | 4607 | 2,4 |
| Виправні роботи | 10346 | 5,1 | 4390 | 2,3 |
| Штраф | 6254 | 3,1 | 10510 | 5,4 |
| Позбавлення права обіймати певні посади | 3686 | 1,8 | 2586 | 1,3 |
| Арешт | 374 | 0,2 | 1674 | 0,9 |
| Громадські роботи | 138 | 0,1 | 1794 | 0,9 |
| тримання в дисциплінарному батальйоні | 17 | 0,0 | 137 | 0,1 |
| Інші види покарання | 76597 | 38,0 | 107105 | 55,3 |
| Всього засуджено | 201627 | 100,0 | 194212 | 100,0 |
Атрибутивні ряди розподілу характеризують склад сукупності за істотними ознаками. Якщо їх побудувати за декілька періодів, то можна прослідити зміну структури явища у часі. (див. табл. 1).
У варіаційному ряді, де розподіл здійснюється за кількісною ознакою, окремі значення варіюючої ознаки називаються варіантами, а кількість одиниць спостереження кожної групи – частотами. Частоти показують, скільки разів повторюються окремі значення варіантів. Залежно від групувальної ознаки варіаційні ряди можуть бути перервними (дискретними) і безперервними (інтервальними).
Варіююча ознака може бути виражена числами по-різному. Якщо вона приймає лише значення цілого числа (наприклад, кількість засуджених по кримінальній справі, кількість дітей в сім`ї, кількість попередніх судимостей), то такий ряд розподілу має назву дискретного або перервного. (табл. 2).
Таблиця 2. Склад розглянутих справ за кількістю засуджених
| Кількість засуджених по справі, чол. | Кількість розглянутих кримінальних справ | У% до всього | Кумулятивна (нагромаджена) кількість розглянутих справ |
| 1 | 20 | 33,3 | 20 |
| 2 | 14 | 23,3 | 34 (20 + 14) |
| 3 | 12 | 20,0 | 46 (34 + 12) |
| 4 | 10 | 16,7 | 56 (46 + 10) |
| 5 | 4 | 6,7 | 60 (56 + 4) |
| Всього | 60 | 100,0 |
У першій колонці таблиці 2 наведені варіанти перервного (дискретного) варіаційного ряду, у другій колонці – частоти варіаційного ряду, в третій – частості. Ясно, що не може бути 1,5 або 2,5 засуджених по конкретній кримінальній справі.
Якщо варіююча ознака може змінюватися безперервно, може приймати значення у десятих та сотих частках цілого, то такий ряд розподілу має назву безперервного. Це, наприклад, вік особи, її зріст, величина заробітної плати, розмір житлової площі, яка приходиться на одного мешканця, тощо. В цьому випадку частоти відносяться не до окремого значення ознаки, як у дискретних рядах, а до всього інтервалу.
Прикладом безперервного ряду розподілу може бути вік осіб, які вчинили злочини, так як варіанти можуть приймати різні значення (роки, місяці, дні та години). Для вивчення і побудови безперервного варіаційного ряду встановлюють інтервали (від … до…). Тому безперервні варіаційні ряди розподілу називають інтервальними. Наведемо приклад безперервного варіаційного ряду розподілу (табл. 3).
Таблиця 3. Розподіл осіб, які вчинили злочини, за віком
| Вік, роки | Кількість, % |
| 14 – 18 | 12,0 |
| 18 – 25 | 25,5 |
| 25 – 30 | 21,5 |
| 30 – 50 | 34,0 |
| 50 і старше | 7,0 |
| Всього | 100,0 |
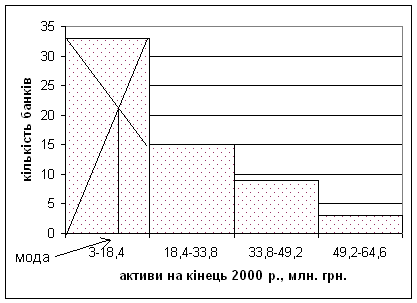
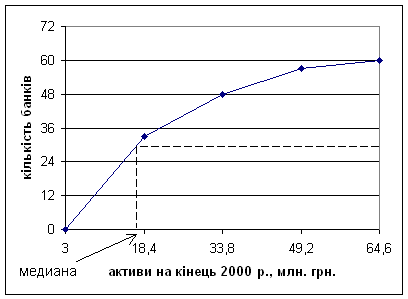
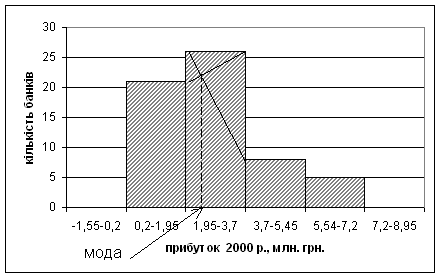
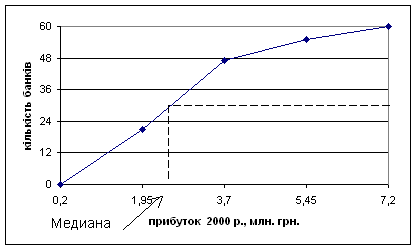
Варіаційні і атрибутивні ряди розподілу у статистичних дослідженнях мають самостійне значення при обчисленні узагальнюючих показників (відносних та середніх величин), а також при використанні графічного зображення (побудови полігона, гістограми та кумуляти) з метою наочного уявлення характеру розподілу сукупності.
Похожие работы
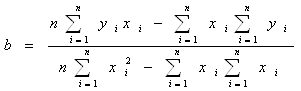
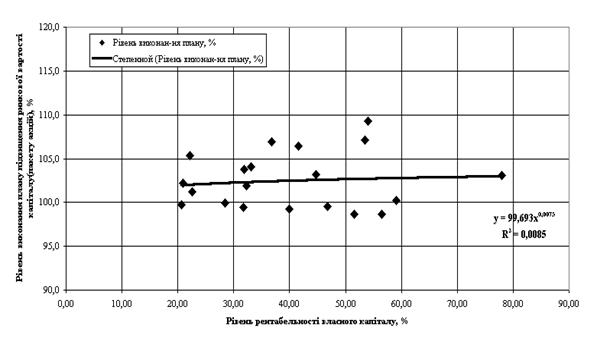
... , то 60% варіації залежної величини пояснюється варіацією незалежного параметра кореляції і зв’язок є щільним. Розділ 2. Аналіз статистичного спостереження характеристик вибірки комерційних банків 2.1 Результати первинного статистичного спостереження показників діяльності комерційних банків Згідно з вихідними даними, в табл.2.1 наведені результати статистичного спостереження показників ді ...
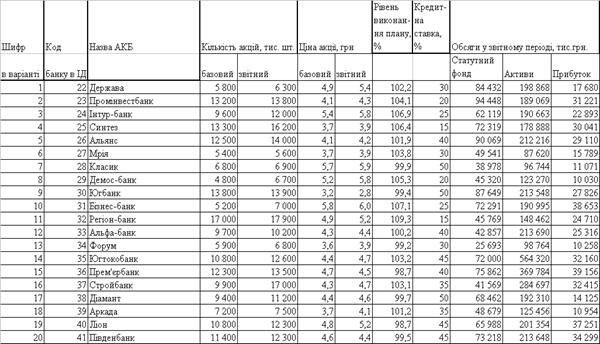
... та темпами росту агрегатних комплексів. На основі регресійного аналізу взаємозв ' язку середніх величин факторних величин (активів) та результатних величин (прибутку) розраховані статистичні коефіцієнти рентабельності роботи комерційних банків у приведеній статистичній виборці. Вихідні індивідуальні данні В табл.1 наведені розраховані згідно методичних вказівок вихідні дані для індивідуального ...
... навантаження поділяються на показники антропогенного та природного навантаження. Щоб оцінити антропогенне навантаження на довкілля, застосовують показники: · видобутку (збору врожаю) окремих природних ресурсів; · що характеризують кiлькiсть викидів і скидів забруднюючих речовин та вiдходiв у атмосферне повітря, водні ресурси та в землю; · що характеризують кiлькiсть використовуваних ...
... дисципліну, яку він назвав статистикою. Основним змістом цього курсу було опис політичного стану та визначних пам'яток держави. Цей напрямок розвитку статистики одержав назву опису вального. Зміст, задачі та предмет вивчення статистики в розумінні Г. Ахенваля були ще далекі від сучасного погляду на статистику як науку. Значно ближче до сучасного розуміння статистики стала англійська школа полі ...

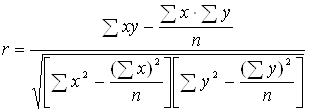
0 комментариев