Задача 7
Задача 11
Вычисляем промежуточные величины для вычисления распределения переменной величины Z=Х-Y (разности двух случайных величин), используя табл.2
Записываем закон распределения случайной величины Z=X-Y в табл.3
Вычисления производим в табличной форме (табл.7)
Результаты вычислений иллюстрирует график рис.3
Навигация
Задача 7
Математические вычисления
11063
знака
11
таблиц
4
изображения
7. Задача 7
Вычислить неопределенный интеграл от рациональной дроби
Решение
1. Найдем производную знаменателя:
2. Выделим в числителе выражение 
, для этого умножим знаменатель на 2 и умножим дробь на 
, чтобы значение дроби не изменилось, и вынесем 
за знак интеграла.
3. Запишем число 
, как 
, получим:
4. Разлагаем подынтегральное выражение на сумму элементарных дробей:
5. Вычислим интеграл 
, для этого выражение внесем под знак дифференциала. Интеграл принимает табличный вид:
6. Вычислим интеграл 
, для этого выделим в знаменателе полный квадрат.
Интеграл принимает табличный вид:
7. Записываем решение:
8. Задача 8
Вычислить определенный интеграл методом интегрирования по частям
Решение
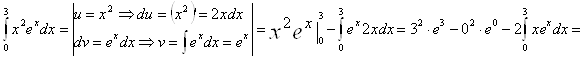
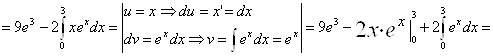
9. Задача 9
По заданным координатам вершинам А, В, С треугольника определить его длины сторон, углы и площадь
А(-5; -5; 3);В(-4; 1; 1);С(1; 4; 0)
Решение
1. Записываем стороны треугольника в форме линейных разложений векторов и строим векторную схему треугольника (рис.1):
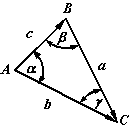
Рис. 2 Схема треугольника
2 Вычисляем длины сторон:
3. Определяем углы треугольника,
следовательно, 
=23.3o
следовательно, 
25,4о
Угол 
по формуле 
.
Следовательно, 
, 
4. Проверяем достоверность вычисления углов треугольника
следовательно, все расчеты выполнены правильно.
5. Вычисляем площадь треугольника:
10. Задача 10
Найти для заданной матрицы 
присоединенную 
и обратную 
матрицы
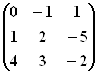
Решение
1.Вычисляем определитель матрицы
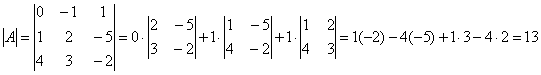
Итак, матрица неособенная и для нее существует обратная матрица 
.
2. Вычисляем для всех элементов матрицы 
алгебраические дополнения:
3. Записываем присоединенную матрицу:
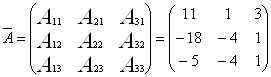
4. Вычисляем обратную матрицу
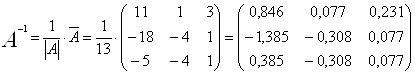
5. Проверяем достоверность вычисления обратной матрицы, умножая ее на исходную матрицу
=
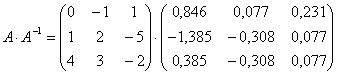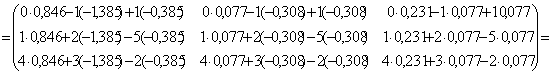
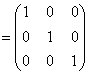
Получили единичную матрицу, следовательно, задача решена верно.
Похожие работы
... наиболее часто используемые при аналитических преобразованиях, располагаются в его системном ядре – части программного обеспечения системы аналитических вычислений, постоянно находящейся в памяти компьютера. К ним относятся команды, выполняющие разнообразные преобразования выражений, получающие решение уравнений и систем уравнений, дифференцирующие функции и т.д. В данной работе вводятся команды, ...
... системам линейных алгебраических уравнений с более чем одной неизвестной; MATLAB решает такие уравнения без вычисле-ния обратной матрицы. Хотя это и не является стандартным математическим обозначением, система MATLAB использует терминологию, связанную с обычным делением в одномерном случае, для описания общего случая решения совместной системы нескольких линейных уравнений. Два символа деления / ...
... Работа с демонстрационными примерами с командной строки Вызов списка демонстрационных примеров Одним из самых эффективных методов знакомства со сложными математическими системами является ознакомление со встроенными примерами их применения. Система MATLAB содержит многие сотни таких примеров – по примеру практически на каждый оператор или функцию. Наиболее поучительные примеры можно найти ...
... классики полезно вспомнить о потенциальном резерве времени, который объективно появляется при использовании систем автоматизации математических расчетов, и использовать этот резерв для резкого расширения круга изучаемых задач и методов вычислений. Незаменима роль системы Derive для интенсификации обучения при подготовке к вступительным экзаменам по математике. Ситуация известна: школьный курс ...
0 комментариев