Навигация
Равноправность строк и столбцов
1. Равноправность строк и столбцов.
Определение 1. Транспонированием определителя называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования.
Определитель, полученный в результате транспонирования, называется транспонированным по отношению к исходному и обозначается ![]() .
.
Свойство 1. При транспонировании величина определителя сохраняется, то есть ![]() .
.
Доказательство этого свойства вытекает из того, что разложение определителя по первой строке тождественно совпадает с разложением по первому столбцу. Данное свойство указывает на равноправность строк и столбцов, поэтому все дальнейшие свойства можно рассматривать лишь для строк.
2. Антисимметрия при перестановке двух строк.
Свойство При перестановке местами двух строк определитель сохраняет свою абсолютную величину, но меняет знак на противоположный.
Докажем для определителя второго порядка. Действительно,
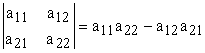 ;
; 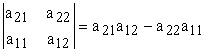 .
.
Для определителя ![]() -го порядка докажем это свойство по индукции. Пусть свойство справедливо для определителя
-го порядка докажем это свойство по индукции. Пусть свойство справедливо для определителя ![]() -го порядка. Разложим определитель
-го порядка. Разложим определитель ![]() -го порядка по любой строке, отличной от переставленных. Тогда переставленные строки входят во все миноры, на которые умножаются элементы
-го порядка по любой строке, отличной от переставленных. Тогда переставленные строки входят во все миноры, на которые умножаются элементы ![]() , но эти миноры являются определителями
, но эти миноры являются определителями ![]() -го порядка и меняют свой знак при перестановке строк. Следовательно, и определитель
-го порядка и меняют свой знак при перестановке строк. Следовательно, и определитель ![]() -го порядка также меняет свой знак.
-го порядка также меняет свой знак.
Определение Некоторая строка (![]() ) является линейной комбинацией строк (
) является линейной комбинацией строк (![]() ) и (
) и (![]() ) с коэффициентами
) с коэффициентами ![]() и
и ![]() , если
, если ![]() .
.
Пользуясь этим определением, перейдем к самому свойству.
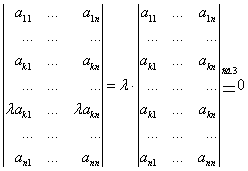
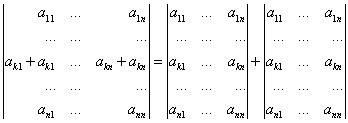
Свойство 3. Если в определителе ![]() -го порядка
-го порядка ![]() некоторая строка
некоторая строка ![]() (
(![]() ) является линейной комбинацией двух строк (
) является линейной комбинацией двух строк (![]() ) и (
) и (![]() ) с коэффициентами
) с коэффициентами ![]() и
и ![]() , то
, то ![]() , где
, где ![]() - определитель, у которого
- определитель, у которого ![]() -ая строка равна (
-ая строка равна (![]() ), а все остальные - те же, что и у
), а все остальные - те же, что и у ![]() , а
, а ![]() - определитель, у которого
- определитель, у которого ![]() -ая строка равна (
-ая строка равна (![]() ), а все остальные - те же, что и у
), а все остальные - те же, что и у ![]() .
.
Для доказательства разложим каждый из определителей по ![]() -ой строке. Очевидно, что у всех разложений миноры
-ой строке. Очевидно, что у всех разложений миноры ![]() соответствующих элементов будут одинаковы. Вычислим
соответствующих элементов будут одинаковы. Вычислим ![]() :
:
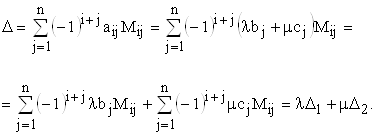
Итак, свойство доказано. Очевидно, оно справедливо и для столбцов.
Приведенные три свойства называются основными. Остальные являются их следствиями.
Свойство 4. Умножение всех элементов некоторой строки или столбца определителя на число ![]() равносильно умножению определителя на число
равносильно умножению определителя на число ![]() .
.
Для доказательства положим в свойстве 3 ![]() , тогда получим
, тогда получим ![]() . Значит, общий множитель всех элементов некоторого ряда можно выносить за определитель.
. Значит, общий множитель всех элементов некоторого ряда можно выносить за определитель.
Свойство 5. Если все элементы некоторой строки или столбца определителя равны 0, то и сам определитель равен 0.
Для доказательства разложим определитель по нулевому ряду.
Свойство 6. Определитель с двумя равными строками или столбцами равен 0.
Действительно, переставив местами равные строки или столбцы, получим тот же определитель, но по свойству 2 его знак изменится на противоположный. Итак, с одной стороны ![]() , а с другой
, а с другой ![]() . Следовательно,
. Следовательно, ![]() .
.
Свойство 7. Если соответствующие элементы двух строк или столбцов определителя пропорциональны, то определитель равен нулю.
Действительно, согласно свойству 4 общий множитель можно выносить за определитель, и мы получим определитель с двумя равными строками, который по свойству 6 равен нулю.
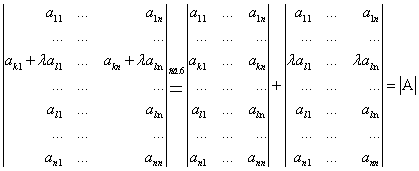
Свойство 8. Если к элементам некоторой строки или столбца определителя прибавить соответствующие элементы другой строки или столбца, умноженные на произвольный множитель ![]() , то величина определителя не изменится.
, то величина определителя не изменится.
Доказательство. Рассмотрим определитель 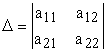 . Прибавим к элементам второй строки элементы первой с коэффициентом
. Прибавим к элементам второй строки элементы первой с коэффициентом ![]() :
:
 .
.
Тогда, по свойству 3 получим:
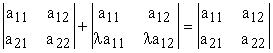 .
.
После перечисления всех свойств определителей введем еще одно определение.
Определение 3. Алгебраическим дополнением данного элемента ![]() определителя
определителя ![]() -го порядка называется число, равное
-го порядка называется число, равное ![]() , которое обозначается
, которое обозначается ![]() .
.
Значит, алгебраическое дополнение отличается от соответствующего минора только лишь знаком. Теперь величину определителя можно вычислить с помощью формул:
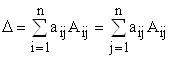 .
.
Пользуясь свойствами, любой определитель можно вычислить не на основании основного правила, а предварительно упростив его (приводя, например, к треугольному виду).
Литература
1. Артамонов Вячеслав Введение в высшую алгебру и аналитическую геометрию. Изд-во: Факториал, Факториал Пресс, 2007. - 128с.
2. Бугров Я.С., Никольский С.М. ВЫСШАЯ МАТЕМАТИКА В 3-х томах Том 1 Элементы линейной алгебры и аналитической геометрии 8-е издание. Издательство: ДРОФА, 2006. - 284с.
3. Рябушко А.П., Бархатов В.В., Державец В.В., Юруть И.Е. Индивидуальные задания по высшей математике. В 4 частях. Часть 1. Линейная и векторная алгебра. Аналитическая геометрия. Дифференциальное исчисление функций одной переменной. Минск: Высшая школа, 2007.
4. Черненко В.Д. Высшая математика в примерах и задачах. В трех томах. ПОЛИТЕХНИКА, 2003.
5. Шипачев В.С. Высшая математика изд.7 Изд-во: ВЫСШАЯ ШКОЛА, 2005. - 479с.
Похожие работы
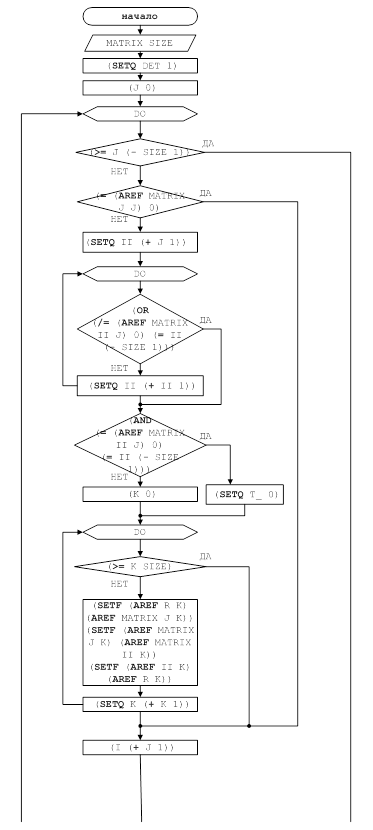
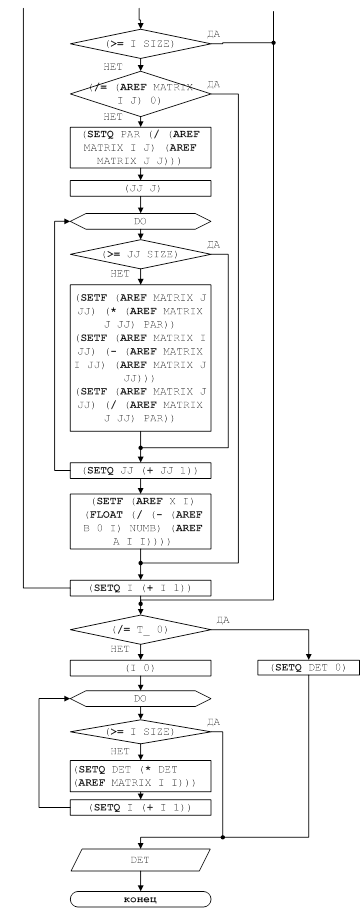
... курсовой работы является реализация вычисления определителя методом исключения Гаусса. 1. Постановка задачи Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель. Вычисление определителя матрицы заключается в выполнении над матрицей алгоритма Гаусса для решения систем линейных алгебраических уравнений. В результате выполнения алгоритма получаем диагональную ...
... ней примыкают задачи вычисления определителей и элементов обратной матрицы, которые иногда называют второй и третьей основными задачами линейной алгебры. В данной работе описаны методы вычисления определителя матрицы и разработана программа для его вычисления с использованием компьютера, основанная на применении метода Гаусса с выбором главного элемента. 1. ВЫБОР И ОБОСНОВАНИЕ ЧИСЛЕННОГО МЕТОДА ...
... равен произведению определителй множителей. Это следует из Теоремы при Заключение В данной работе рассмотрена основная теория матриц и доказательство теоремы Коши-Бине. Также представлено применение данной теоремы при нахождении определителя произведения двух прямоугольных матриц в программе написанной на языке программирования Дельфи с возможностью ввода матриц вручную и подгрузкой из файла. ...
... так и ВּА, существует, так как матрицы согласованны: ·==·==; ·==·== = = АּВ=ВּА, т. е. данные матрицы коммутирующие. ЛЕКЦИЯ 2. ОПРЕДЕЛИТЕЛИ План 1. Определители квадратной матрицы и их свойства. 2. Теоремы Лапласа и аннулирования. Ключевые понятия Алгебраическое дополнение элемента определителя. Минор элемента определителя. ...
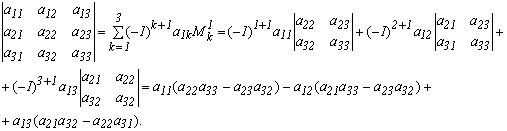


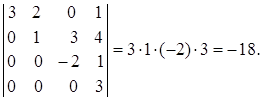
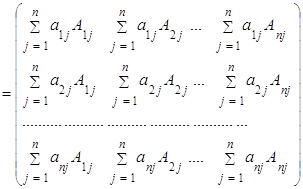
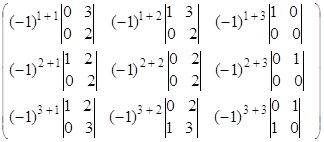
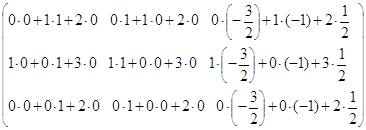
0 комментариев