Элементы теории пределов для комплексных чисел

3. Элементы теории пределов для комплексных чисел

В моей работе полиномы рассматриваются только над полями и  как функции от комплексной или вещественной переменной, так что моя работа является скорее главой математического анализа, а не алгебры, хотя теорема о существовании корня у любого отличного от константы полинома с комплексными коэффициентами (т.е. установление алгебраической замкнутости поля ) носит название основной теоремы алгебры.

Определение: Пусть задана последовательность комплексных чисел  . Число  называется ее пределом, если для любого действительного числа  существует такой номер , что при  выполняется неравенство . В этом случае пишут lim , а=lim, b=lim. Предельное соотношение lim=c равносильно соотношению , ибо

max  

Последовательность такая, что  R, при некотором R, называется ограниченной.

Для вещественных переменных известная теорема Больцано-Вейерштрасса: из любой ограниченной последовательности можно извлечь сходящуюся подпоследовательность. То же самое верно и для последовательностей, составленных из комплексных чисел.

Действительно, пусть ограниченная последовательность, т.е. , тогда , так что  есть ограниченная последовательность вещественных чисел. Из нее можно выбрать сходящуюся подпоследовательность . Рассмотрим соответствующую подпоследовательность мнимых частей . Она ограничена, и из нее можно извлечь сходящуюся подпоследовательность .

Соответствующая подпоследовательность комплексных чисел имеет сходящиеся последовательности вещественных и мнимых частей и, следовательно, сходятся, и ее предел равен .

4. Доказательство основной теоремы

Прежде чем приступить к формальному доказательству, наметим его идею. Пусть -полином, рассматриваемый как функция от комплексной переменной .Представим себе "график" функции , считая , что значения  изображаются на горизонтальной плоскости, перпендикулярной к плоскости чертежа, а значения  откладываются вверх в направлении оси . Мы установим, что являются непрерывными функциями от на всей плоскости комплексной переменной. Функция от комплексной переменной  называется непрерывной в точке , если достаточно близким к  значениями  соответствует сколь угодно близкие к значения .В более точных терминах - для любого найдется такое , что , как только .

Непрерывность  дает основания представлять себе график  в виде непрерывной поверхности, накрывающей плоскость , и местами доходящей до этой плоскости. Собственно говоря, нам и нужно доказать, что существует такое значение  , в котором , и, тем самым, , т.е. что поверхность  доходит до плоскости в точке . Мы докажем, что если дана точка на поверхности ,которая расположена выше плоскости , то в ее окрестности найдется точка поверхности расположенная ниже данной точки. Тогда останется только доказать, что на поверхности  существует самая низкая точка, скажем, при  . Она не может находиться выше плоскости , ибо тогда она была бы самой низкой точкой. Следовательно,  и , следовательно , т.е.  корень полинома .

Теперь приступим к доказательству основной теоремы, разбив это доказательство на цепочку лемм.

Лемма 1. Дан полином  c нулевым свободным членом.

Тогда для любого найдется такое , что , как только .

Доказательство: Пусть . Тогда

Положим

Если

то

что и требовалось доказать.

Лемма 2. Полином есть непрерывная функция во всех точках плоскости комплексной переменной.

Доказательство: Пусть дан полином и точка _. Расположим полином по степеням

,

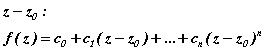Тогда так что

Правая часть есть полином от  с нулевым свободным членом.

По лемме 1 для любого  найдется такое, что как только  что и требовалось доказать.

Лемма 3. Модуль полинома есть непрерывная функция.

Доказательство: Из неравенства  следует, что для данного  то , которое "обслуживает" , подходит и для . Действительно, при  имеем

Лемма 4. (о возрастании модуля полинома). Если -полином, отличный от константы, то для любого М>0 существует такое R>0, что M,как только .

Это означает, что любая горизонтальная плоскость отрезает от поверхности  конечный кусок, накрывающий часть круга |z|≤R.

Доказательство: Пусть

где полином от c нулевым свободным членом.

В силу леммы 1 для  найдется такое , что при , будет . Модуль  может быть сделан сколь угодно большим, именно, при  будет . Возьмем  Тогда при  будет

 и  так что

Лемма 5. Точная нижняя грань значений  достигается, т.е. существует такое, что  при всех .

Доказательство: Обозначим точную нижнюю грань  через . Возьмем последовательностью  стремящихся к сверху. Каждая из этих чисел не является нижней гранью значений , ибо -точная нижняя грань. Поэтому найдутся  такие, что  . Воспользуемся теперь леммой о возрастании модуля. Для  найдем такое , что при  будет  Отсюда следует, что  при все . Последовательностью  оказалась ограниченной, и из нее можно извлечь сходящуюся подпоследовательность  . Пусть ее предел равен  . Тогда  в силу непрерывности . Кроме того, . Поэтому  Итак , что и требовалось доказать.

Лемма 6. (Лемма Даламбера). Пусть  полином отличный от константы, и пусть . Тогда найдется такая точка, что

Геометрический смысл этой леммы: если на поверхности  дана точка, находящаяся выше плоскости , то на ней найдется другая точка, расположенная ниже первой.

Доказательство: Расположим полином  по степеням

Тогда  Идея доказательства состоит в том, чтобы за счет первого отличного от нуля слагаемого "откусить кусочек" от , а влияние дальнейших слагаемых сделать незначительным. Пусть  – первое отличное от нуля слагаемое после , так что  (если k>1). Такое слагаемое имеется, так как  не константа. Тогда

 +

+( +…+ ))=

=c₀ (1+ +).

Здесь

=

есть полином от  с нулевым свободным членом. По лемме 1 для = найдется такое ,что ||<, как только ||<. Положим =() и  . Тогда

.

Выберем  так, что . Для этого нужно взять . Далее, положим , т.е. возьмем . При таком выборе будет . Теперь положим

 при  и . Тогда  и

||=.

Лемма доказана.

Заметим, что с тем же успехом мы могли бы взять  при  так что при k>1 (т.е. в случае, когда -корень кратности  полинома )имеется k направлений спуска по поверхности . Они разделяются  направлениями подъема при

Действительно, в этих направлениях

 и

Так что если  есть корень производной кратности , то поверхность  в окрестности точки  "гофрирована" так, что на ней имеется  "долин" cпуска, раздельных  "хребтами" подъема.

Теорема: Полином с комплексными коэффициентами, отличный от постоянной, имеет по меньше мере один комплексный корень (т.е. поле , комплексных чисел алгебраически замкнуто).

Доказательство: Пусть - данный полином, отличный от константы. Пусть, далее,  и - точка, в которой ; Она существует по лемме 5. Тогда  ибо иначе, согласно лемме 6, нашлась бы такая точка  что  невозможно.

СПИСОК ЛИТЕРАТУРЫ

Д.К.Фадеев Лекции по алгебре. - СПб.: Изд-во "Лань", 2007. - 416с.

Л.Д.Кудрявцев Курс математического анализа. – М.: Изд-во "Высш. Школа", 1981г. – 687с.

А.Г.Курош Курс высшей алгебры. – М.: Изд-во "Наука", 1971 г. – 431с.