Навигация
Приближённое решение алгебраических и трансцендентных уравнений
![]() Приближённое решение алгебраических и трансцендентных уравнений
Приближённое решение алгебраических и трансцендентных уравнений
1. Общая постановка задачи. ![]() Найти действительные корни уравнения
Найти действительные корни уравнения ![]() , где
, где ![]() - алгебраическая или трансцендентная функция.
- алгебраическая или трансцендентная функция.
Точные методы решения уравнений подходят только к узкому классу уравнений (квадратные, биквадратные, некоторые тригонометрические, показательные, логарифмические).
В общем случае решение данного уравнения находится приближённо в следующей последовательности:
1) отделение (локализация) корня;
![]() 2) приближённое вычисление корня до заданной точности.
2) приближённое вычисление корня до заданной точности.
2. Отделение корня. ![]()
![]() Отделение действительного корня уравнения
Отделение действительного корня уравнения ![]() - это нахождение отрезка
- это нахождение отрезка ![]() , в котором лежит только один корень данного уравнения. Такой отрезок называется отрезком изоляции (локализации) корня.
, в котором лежит только один корень данного уравнения. Такой отрезок называется отрезком изоляции (локализации) корня.
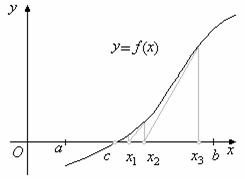
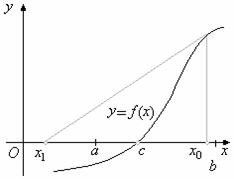
![]() Наиболее удобным и наглядным является графический метод отделения корней:
Наиболее удобным и наглядным является графический метод отделения корней:
1) строится график функции ![]() , и определяются абсциссы точек пересечения этого графика с осью
, и определяются абсциссы точек пересечения этого графика с осью ![]() , которые и являются корнями уравнения
, которые и являются корнями уравнения ![]() ;
;
2) если ![]() - сложная функция, то её надо представить в виде
- сложная функция, то её надо представить в виде ![]() так, чтобы легко строились графики функций
так, чтобы легко строились графики функций ![]() и
и ![]() . Так как
. Так как ![]() , то
, то ![]() . Тогда абсциссы точек пересечения этих графиков и будут корнями уравнения
. Тогда абсциссы точек пересечения этих графиков и будут корнями уравнения ![]() .
.
Пример.![]() Графически отделить корень уравнения
Графически отделить корень уравнения ![]() .
.
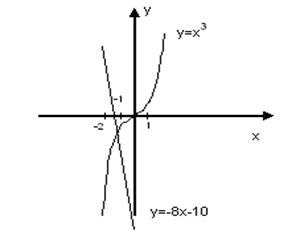 |
Решение. Представим левую часть уравнения в виде
![]() Абсцисса точки пересечения графиков находится на отрезке
Абсцисса точки пересечения графиков находится на отрезке ![]() , значит корень уравнения
, значит корень уравнения ![]() .
.
3. ![]() Уточнение корня.
Уточнение корня.
![]() Если искомый корень уравнения
Если искомый корень уравнения ![]() отделён, т.е. определён отрезок
отделён, т.е. определён отрезок ![]() , на котором существует только один действительный корень уравнения, то далее необходимо найти приближённое значение корня с заданной точностью.
, на котором существует только один действительный корень уравнения, то далее необходимо найти приближённое значение корня с заданной точностью.
![]() Такая задача называется задачей уточнения корня.
Такая задача называется задачей уточнения корня.
![]() Уточнение корня можно производить различными методами:
Уточнение корня можно производить различными методами:
![]() 1) метод половинного деления (бисекции);
1) метод половинного деления (бисекции);
![]() 2) метод итераций;
2) метод итераций;
![]() 3) метод хорд (секущих);
3) метод хорд (секущих);
![]() 4) метод касательных (Ньютона);
4) метод касательных (Ньютона);
![]() 5) комбинированные методы.
5) комбинированные методы.
Похожие работы
... - в методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона) Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1.5) Графики ...
... «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных ...
... - функции f. Дальше, имеем: . Отсюда , где W'(x) - транспонированная матрица Якоби. Поэтому окончательно , причем . 3. Программная реализация итерационных методов Реализация алгоритмов итерационных методов решения систем нелинейных уравнений будет показана на примере системы: 3.1 Метод простых итераций Приведём систему к виду: Проверим условие ...
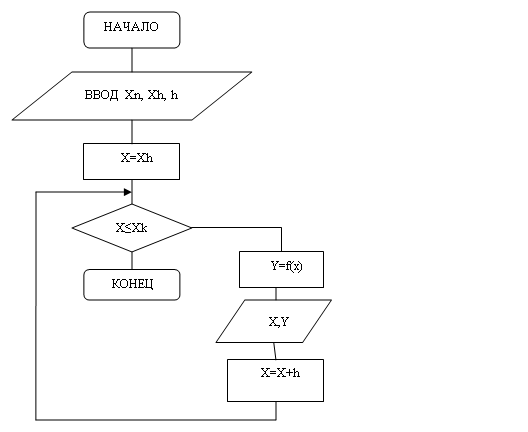
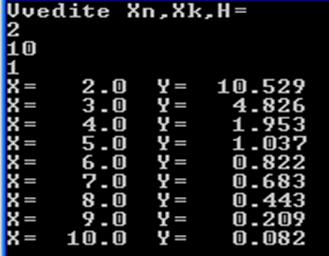
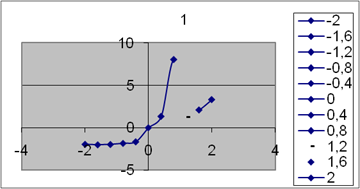
... 1,' Y=',Y: 8: 3); X: =X+H; until X>=Xk+H/2; readkey; end. Блок-схема к заданию: Результаты вычислений: Задание 1 (б) Решение программы вычисления функции с условием Решение уравнения в табличном редакторе Microsoft Excel Для реализации задачи необходимо использовать логическую функцию ЕСЛИ, которая возвращает одно значение, если заданное условие при вычислении дает ...


0 комментариев