Навигация
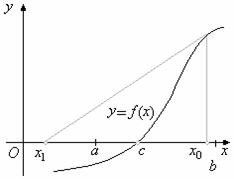
Метод половинного деления (бисекции)
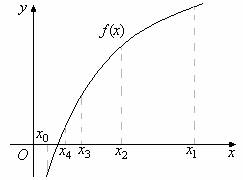
![]() Отрезок изоляции корня можно уменьшить путём деления его пополам.
Отрезок изоляции корня можно уменьшить путём деления его пополам.
![]() Такой метод можно применять, если функция
Такой метод можно применять, если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на его концах принимает значения разных знаков, т.е. выполняется условие
и на его концах принимает значения разных знаков, т.е. выполняется условие ![]() (1).
(1).
![]() Разделим отрезок
Разделим отрезок ![]() пополам точкой
пополам точкой ![]() , которая будет приближённым значением корня
, которая будет приближённым значением корня ![]() .
.
![]() Для уменьшения погрешности приближения корня уточняют отрезок изоляции корня. В этом случае продолжают делить отрезки, содержащие корень, пополам.
Для уменьшения погрешности приближения корня уточняют отрезок изоляции корня. В этом случае продолжают делить отрезки, содержащие корень, пополам.
![]() Из отрезков
Из отрезков ![]() и
и ![]() выбирают тот, для которого выполняется неравенство (1).
выбирают тот, для которого выполняется неравенство (1).
![]() В нашем случае это отрезок
В нашем случае это отрезок ![]() , где
, где ![]() .
.
![]() Далее повторяем операцию деления отрезка пополам, т.е. находим
Далее повторяем операцию деления отрезка пополам, т.е. находим ![]() и так далее до тех пор, пока не будет достигнута заданная точность
и так далее до тех пор, пока не будет достигнута заданная точность ![]() . Т.е. до тех пор, пока не перестанут изменяться сохраняемые в ответе десятичные знаки или до выполнения неравенства
. Т.е. до тех пор, пока не перестанут изменяться сохраняемые в ответе десятичные знаки или до выполнения неравенства ![]() .
.
![]() Достоинство метода: простота (достаточно выполнения неравенства (1)).
Достоинство метода: простота (достаточно выполнения неравенства (1)).
![]() Недостаток метода: медленная сходимость результата к заданной точности.
Недостаток метода: медленная сходимость результата к заданной точности.
![]() Пример. Решить уравнение
Пример. Решить уравнение ![]() методом половинного деления с точностью до 0,001.
методом половинного деления с точностью до 0,001.
![]() Решение.
Решение.![]() Известен отрезок изоляции корня
Известен отрезок изоляции корня ![]() и заданная точность
и заданная точность ![]() . По уравнению составим функцию
. По уравнению составим функцию ![]() .
.
Найдём значения функции на концах отрезка: ![]()
![]() ,
, ![]() .
.
Проверим выполнение неравенства (1): ![]() - условие выполняется, значит можно применить метод половинного деления.
- условие выполняется, значит можно применить метод половинного деления.
Найдём середину отрезка ![]() и вычислим значение функции в полученной точке:
и вычислим значение функции в полученной точке:
![]() ,
, ![]() .
.
Среди значений ![]()
![]() и
и ![]() выберем два значения разных знаков, но близких друг к другу. Это
выберем два значения разных знаков, но близких друг к другу. Это ![]() и
и ![]() . Следовательно, из отрезков
. Следовательно, из отрезков ![]() и
и ![]() выбираем тот, на концах которого значения функции разных знаков. В нашем случае это отрезок
выбираем тот, на концах которого значения функции разных знаков. В нашем случае это отрезок ![]() и опять находим середину отрезка и вычисляем значение функции в этой точке:
и опять находим середину отрезка и вычисляем значение функции в этой точке:
![]() ,
, ![]() ,
, ![]() ,
, ![]() - заданная точность результата не достигнута, продолжим вычисления.
- заданная точность результата не достигнута, продолжим вычисления.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() - заданная точность результата достигнута, значит, нашли приближённое значение корня
- заданная точность результата достигнута, значит, нашли приближённое значение корня ![]() .
.
Ответ: корень уравнения ![]() с точностью до 0,001.
с точностью до 0,001.
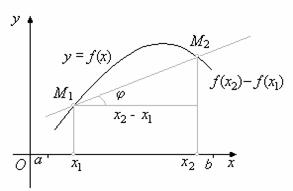
Этот метод применяется при решении уравнений вида ![]() , если корень уравнения отделён, т.е.
, если корень уравнения отделён, т.е. ![]() и выполняются условия:
и выполняются условия:
1) ![]() (функция
(функция ![]() принимает значения разных знаков на концах отрезка
принимает значения разных знаков на концах отрезка ![]() );
);
2) производная ![]() сохраняет знак на отрезке
сохраняет знак на отрезке ![]() (функция
(функция ![]() либо возрастает, либо убывает на отрезке
либо возрастает, либо убывает на отрезке ![]() ).
).
Первое приближение корня находится по формуле: ![]() .
.
Для следующего приближения из отрезков ![]() и
и ![]() выбирается тот, на концах которого функция
выбирается тот, на концах которого функция ![]() имеет значения разных знаков.
имеет значения разных знаков.
Тогда второе приближение вычисляется по формуле:
![]() , если
, если ![]() или
или ![]() , если
, если ![]() .
.
Вычисления продолжаются до тех пор, пока не перестанут изменяться те десятичные знаки, которые нужно оставить в ответе.
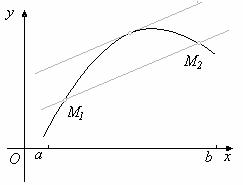
6. Метод касательных (Ньютона).Этот метод применяется, если уравнение ![]() имеет корень
имеет корень ![]() , и выполняются условия:
, и выполняются условия:
1) ![]() (функция принимает значения разных знаков на концах отрезка
(функция принимает значения разных знаков на концах отрезка ![]() );
);
2) производные ![]() и
и ![]() сохраняют знак на отрезке
сохраняют знак на отрезке ![]() (т.е. функция
(т.е. функция ![]() либо возрастает, либо убывает на отрезке
либо возрастает, либо убывает на отрезке ![]() , сохраняя при этом направление выпуклости).
, сохраняя при этом направление выпуклости).
На отрезке ![]() выбирается такое число
выбирается такое число ![]() , при котором
, при котором ![]() имеет тот же знак, что и
имеет тот же знак, что и ![]() , т. е. выполняется условие
, т. е. выполняется условие ![]() . Таким образом, выбирается точка с абсциссой
. Таким образом, выбирается точка с абсциссой ![]() , в которой касательная к кривой
, в которой касательная к кривой ![]() на отрезке
на отрезке ![]() пересекает ось
пересекает ось ![]() . За точку
. За точку ![]() сначала удобно выбирать один из концов отрезка.
сначала удобно выбирать один из концов отрезка.
Первое приближение корня определяется по формуле: ![]() .
.
Второе приближение корня определяется по формуле: ![]() .
.
Вычисления ведутся до совпадения десятичных знаков, которые необходимы в ответе, или при заданной точности ![]() - до выполнения неравенства
- до выполнения неравенства ![]() .
.
Достоинства метода: простота, быстрота сходимости.
Недостатки метода: вычисление производной и трудность выбора начального положения.
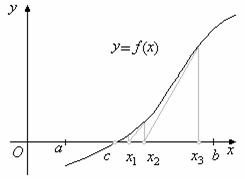
7. Комбинированный метод хорд и касательных.Если выполняются условия:
1) ![]() ,
,
2) ![]() и
и ![]() сохраняют знак на отрезке
сохраняют знак на отрезке ![]() ,
,
то приближения корня ![]() уравнения
уравнения ![]() по методу хорд и по методу касательных подходят к значению этого корня с противоположных сторон. Поэтому для быстроты нахождения корня удобно применять оба метода одновременно. Т.к. один метод даёт значение корня с недостатком, а другой – с избытком, то достаточно легко получить заданную степень точности корня.
по методу хорд и по методу касательных подходят к значению этого корня с противоположных сторон. Поэтому для быстроты нахождения корня удобно применять оба метода одновременно. Т.к. один метод даёт значение корня с недостатком, а другой – с избытком, то достаточно легко получить заданную степень точности корня.
1. Вычислить значения функции ![]() и
и ![]() .
.
2. Проверить выполнение условия ![]() . Если условие не выполняется, то неправильно выбран отрезок
. Если условие не выполняется, то неправильно выбран отрезок ![]() .
.
3. Найти производные ![]() и
и ![]() .
.
4. Проверить постоянство знака производных на отрезке ![]() . Если нет постоянства знака, то неверно выбран отрезок
. Если нет постоянства знака, то неверно выбран отрезок ![]() .
.
5. Для метода касательных выбирается за ![]() тот из концов отрезка
тот из концов отрезка ![]() , в котором выполняется условие
, в котором выполняется условие ![]() , т.е.
, т.е. ![]() и
и ![]() одного знака.
одного знака.
6. Приближения корней находятся:
а) по методу касательных: ![]() ,
,
б) по методу хорд: ![]() .
.
7. Вычисляется первое приближение корня: ![]() .
.
8. Проверяется выполнение условия: ![]() , где
, где ![]() - заданная точность.
- заданная точность.
Если условие не выполняется, то нужно продолжить применение метода по схеме 1-8.
В этом случае отрезок изоляции корня сужается и имеет вид ![]() . Приближённые значения корня находятся по формулам:
. Приближённые значения корня находятся по формулам:
![]() и
и ![]() .
.
Вычисления продолжаются до тех пор, пока не будет найдено такое значение ![]() , при котором
, при котором ![]() и
и ![]() совпадут с точностью
совпадут с точностью ![]() .
.
Решение.
1. Вычислим значения функции ![]() на концах отрезка:
на концах отрезка: ![]() ,
, ![]() .
.
2. Проверим выполнение условия: ![]() - условие выполняется.
- условие выполняется.
3. Найдём производные: ![]() и
и ![]()
![]() .
.![]()
4. На отрезке ![]() производные
производные ![]() и
и ![]() , т.е. сохраняют знак, следовательно, условие выполняется.
, т.е. сохраняют знак, следовательно, условие выполняется.
5. Выберем значение ![]() для метода касательных. Т.к.
для метода касательных. Т.к. ![]() и
и ![]() , то
, то ![]() .
.
6. Найдём приближения корня:
а) по методу касательных: ![]()
б) по методу хорд: ![]() .
.
7. Найдём первое приближение корня: ![]() .
.
8. Проверим выполнение условия: ![]() - условие не выполняется, значит нужно продолжить вычисления.
- условие не выполняется, значит нужно продолжить вычисления.
9. Отрезок изоляции корня имеет вид: ![]() .
.
10. Продолжим уточнение корня по схеме. Для этого найдём значения функции на концах суженного отрезка:
![]() ,
, ![]() .
.
11. Проверим условие: ![]() - выполняется, значит можно продолжить применение метода.
- выполняется, значит можно продолжить применение метода.![]()
12. Так как ![]() и
и ![]() на отрезке
на отрезке![]() , то для метода касательных:
, то для метода касательных: ![]() .
.
13. Вычислим значение производной: ![]() .
.
14. Найдём новые значения концов отрезка изоляции:
![]() ,
, ![]() .
.
15. Найдём второе приближение корня: ![]() .
.
16. Проверим выполнение условия: ![]() - неравенство неверное, значит необходимо продолжить вычисления.
- неравенство неверное, значит необходимо продолжить вычисления.
17. Отрезок изоляции корня имеет вид: ![]() .
.
18. Вычислим значения функции:
![]() ,
, ![]() .
.
19. Условие ![]() - выполняется.
- выполняется.
20. Так как ![]() и
и ![]() на
на ![]() , то для метода касательных
, то для метода касательных ![]() .
.
21. Вычислим производную: ![]() .
.
22. Вычислим: ![]() ,
,
![]() .
.
23. Найдём третье приближение корня: ![]() .
.
24. Проверим выполнение неравенства: ![]() - условие выполняется, значит, цель достигнута.
- условие выполняется, значит, цель достигнута.
25. Следовательно, ![]() или
или ![]() - приближённое значение корня с точностью до 0,001.
- приближённое значение корня с точностью до 0,001.
Ответ: ![]() .
.
Похожие работы
... - в методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона) Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1.5) Графики ...
... «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных ...
... - функции f. Дальше, имеем: . Отсюда , где W'(x) - транспонированная матрица Якоби. Поэтому окончательно , причем . 3. Программная реализация итерационных методов Реализация алгоритмов итерационных методов решения систем нелинейных уравнений будет показана на примере системы: 3.1 Метод простых итераций Приведём систему к виду: Проверим условие ...
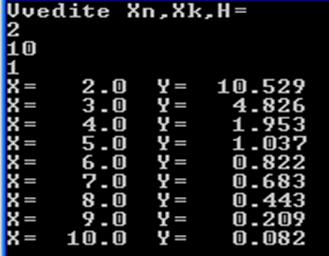
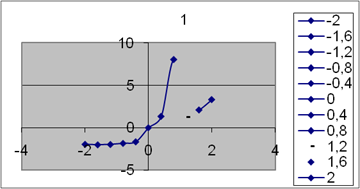
... 1,' Y=',Y: 8: 3); X: =X+H; until X>=Xk+H/2; readkey; end. Блок-схема к заданию: Результаты вычислений: Задание 1 (б) Решение программы вычисления функции с условием Решение уравнения в табличном редакторе Microsoft Excel Для реализации задачи необходимо использовать логическую функцию ЕСЛИ, которая возвращает одно значение, если заданное условие при вычислении дает ...
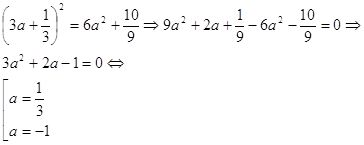
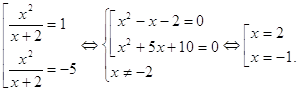
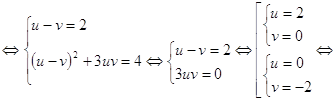


0 комментариев