Навигация
Размахом вариации называется число
4. Размахом вариации называется число
![]() ,
,
где или ![]() – наибольший,
– наибольший, ![]() – наименьший вариант ряда.
– наименьший вариант ряда.
![]()
5. Выборочным средним ![]() называется среднее арифметическое всех значений выборки:
называется среднее арифметическое всех значений выборки:
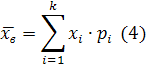
В случае интервального статистического ряда в качестве ![]() следует брать середины интервалов, а
следует брать середины интервалов, а ![]() - соответствующие им частости.
- соответствующие им частости.
![]()
6. Выборочной дисперсией Dвназывается среднее арифметическое квадратов отклонений значений выборки от выборочной средней, т.е.
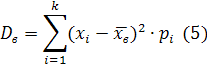
![]()
7. Выборочное среднеквадратическое отклонение выборки определяется формулой:
![]()
8. Эмпирической (статистической) функцией распределения называется функция ![]() , определяющая для каждого значения x частость события
, определяющая для каждого значения x частость события ![]() :
: ![]() . Для нахождения эмпирической функции
. Для нахождения эмпирической функции ![]() записывают в виде:
записывают в виде:
![]()
где n – объем выборке, nx– число наблюдений, меньших х. Согласно (7) определим значения эмпирической функции распределения в выбранных интервалах.
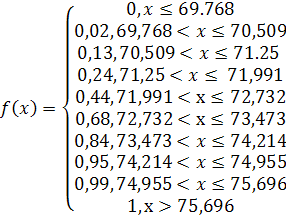
График эмпирической функции распределения имеет вид.
Одной из важных задач математической статистики является установление теоретического закона распределения случайной величины, характеризующей изучаемый признак по эмпирическому распределению, представляющему вариационный ряд.
Проверим при уровне значимости ![]() гипотезу
гипотезу ![]() о том, что исследуемая выборка подчиняется нормальному закону распределения.
о том, что исследуемая выборка подчиняется нормальному закону распределения.
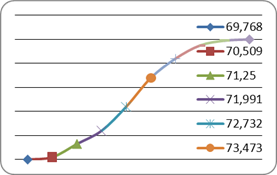
Рисунок 2. График эмпирической функции распределения
Число наблюдений в крайних интервалах меньше 5, поэтому объединим их с соседними. Получим следующий ряд распределения ( n=100).
| Интервалы | Частота k | Середина интервала Xcp |
| 69,768-71,25 | 13 | 70,694 |
| 71,25-71,991 | 11 | 71,62 |
| 71,991-72,732 | 20 | 72,362 |
| 72,732-73,473 | 24 | 73,102 |
| 73,473-74,214 | 16 | 73,844 |
| 74,214-74,955 | 11 | 74,584 |
| 74,955-76,437 | 5 | 75,377 |
Вычислим параметры, определяющие нормальный закон распределения.
![]()
![]()
![]()
Так как случайная величина имеет нормальное распределение, то для расчета вероятностей ![]() попадания случайной величины X в интервал используем функцию Лапласа в соответствии со свойствами нормального распределения:
попадания случайной величины X в интервал используем функцию Лапласа в соответствии со свойствами нормального распределения:
![]()
Полученные результаты приведем в следующей таблице:
| Xi, Xi+1 | 69,768-71,25 | 71,25-71,991 | 71,991-72,732 | 72,732-73,473 | 73,473-74,214 | 74,214-74,955 | 74,955-76,437 |
| ni | 13 | 11 | 20 | 24 | 16 | 11 | 5 |
| n`=n∙pi | 10,2 | 14,5 | 20,92 | 22,46 | 17,69 | 9,03 | 5,2 |
Определим критерий Пирсона:
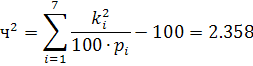
Находим число степеней свободы. По выборке рассчитаны два параметра, значит ![]() . Количество интервалов
. Количество интервалов ![]() . Следовательно,
. Следовательно, ![]() . Зная, что
. Зная, что ![]() , по таблице находим
, по таблице находим ![]() . Поскольку
. Поскольку ![]() считаем гипотезу верной.
считаем гипотезу верной.
Похожие работы
... отклонения полученных результатов от ожидаемых, при известных погрешностях. Средняя арифметическая погрешность измерения физической величины. при - абсолютная погрешность - ого измерения величины . Среднеквадратичное отклонение результата измерения величины Расчётная часть Оценка погрешности при прямых вычислениях величин h и d, произведенные штангенциркулем. № ...
... повторных измерениях остаются постоянными или изменяются закономерно, обычно прогрессируя. Постоянные систематические погрешности свидетельствуют о высоких или недостаточных показателях метрологической надёжности применяемого средства измерения и могут быть устранены (учтены) предусмотренными аппаратурными методами коррекции или введением поправок в результаты измерений. Одной из распространённой ...
... результату измерений из совокупности результатов измерений, выполняемых по одной и той же аттестованной МВИ– приписанные погрешности измерений. 3. Отражающие близость отдельного, экспериментально полученного результата измерений к истинному значению измеряемой величины – статистические оценки характеристик погрешности измерений (статистические оценки погрешности измерений). Нормы погрешности ...
... – оценку дисперсии : (2.3.10) Таким образом мы доказали, что для нормально распределенных данных СКО является лучшей оценкой дисперсии. Обработка результатов совместных измерений При совместных измерениях полученные значения используются для построения зависимостей между измеряемыми величинами. Рассмотрим многофакторный эксперимент, по результатом которого должна быть построена ...
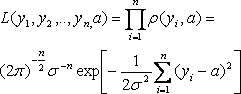


0 комментариев