Навигация
Этап. Определение сокращенной ДНФ
1 этап. Определение сокращенной ДНФ.
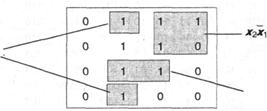
По десятичным эквивалентам запишем 0-кубы :
![]()
Выполним разбиение на подгруппы:
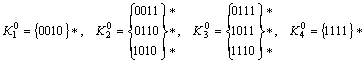 .
.
Строим ![]() -кубы, сравнивая соседние группы (значок (*) указывает на участие данной импликанты в склеивании):
-кубы, сравнивая соседние группы (значок (*) указывает на участие данной импликанты в склеивании):
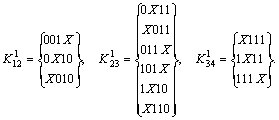
Выполняем разбиение всех ![]() -кубов в зависимости от расположения независимой переменной Х :
-кубов в зависимости от расположения независимой переменной Х :
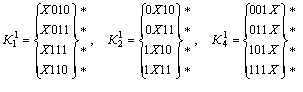 .
.
Выполняем сравнение кубов внутри каждой подгруппы с целью построения ![]() -кубов (значок (*) указывает на участие данной импликанты в склеивании):
-кубов (значок (*) указывает на участие данной импликанты в склеивании):
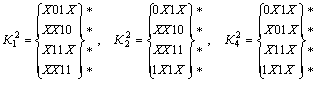 .
.
Выполняем сравнение кубов внутри каждой подгруппы с целью построения ![]() -кубов (значок (*) указывает на участие данной импликанты в склеивании):
-кубов (значок (*) указывает на участие данной импликанты в склеивании):
![]() или
или
![]() .
.
Так как они одинаковы, то ![]() .
.
Запишем сокращенную ДНФ, в которую должны быть включены им-пликанта из К 3 и импликанты, не участвовавшие в склеивании (в нашем случае таких импликант нет) :
![]() .
.
2 этап. Определение тупиковой ДНФ.
Так как все импликанты участвовали в склеивании, и сокращенная ДНФ состоит из одной простой импликанты, то строить таблицу покрытий нет необходимости, т.е.
![]() .
.
Задание 6
Для неориентированного графа ![]() , у которого
, у которого ![]()
![]() ,
, ![]()
а) вычислить числа ![]() ;
;
б) определить хроматическое число ![]() .
.
Решение:
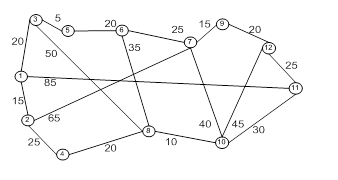
Построим граф:
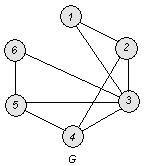
а) Вычислим числа ![]() .
.
1) ![]() :
:
Используя алгоритм выделения пустых подграфов, построим дерево:
Согласно определению ![]() :
:
![]() .
.
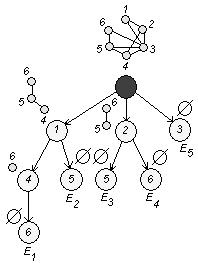
2) ![]() :
:
Используя алгоритм выделения полных подграфов, построим дерево:
Здесь ![]() - полные подграфы. Видно, что мощность носителей всех подграфов равна трем, т.е.
- полные подграфы. Видно, что мощность носителей всех подграфов равна трем, т.е.
![]() .
.
3) ![]() :
:

Построим модифицированную матрицу смежности ![]() заданного графа G :
заданного графа G :
1 2 3 4 5 6
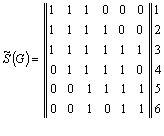
![]() .
.
Находим минимальное число строк, покрывающих все столбцы модифи-цированной матрицы . Таких строк – одна. Следовательно,
![]() .
.
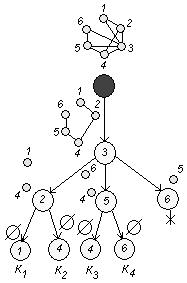
б) Определим хроматическое число ![]() .
.

Согласно алгоритму минимальной раскраски вершин графа, выделим все пустые подграфы графа G , т.е. построим дерево (оно построено в пункте а) ):
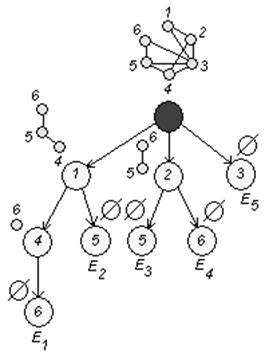
Построим таблицу:
1 2 3 4 5 6
1. {1,4,6} 1 1 1 ![]()
2. {1,5} 1 1
3. {2,5} 1 1 ![]()
4. {2,6} 1 1
5. {3} 1 ![]()
Определяем минимальное число строк, покрывающих все столбцы таблицы. Такими строками могут быть строки 1, 3, 5. Значит,
![]() .
.
Зададимся красками: для множества вершин ![]() - краска синяя (С ), для множества вершин
- краска синяя (С ), для множества вершин ![]() - краска красная ( К ), для множества вершин
- краска красная ( К ), для множества вершин ![]() - краска зеленая ( З ).
- краска зеленая ( З ).
Раскрасим вершины графа G :
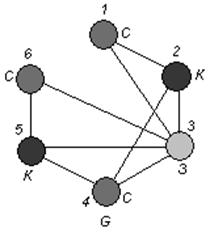
Задание 7
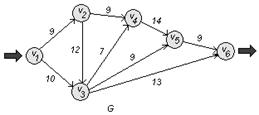
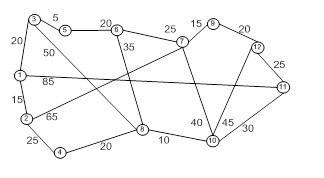
Для заданной сети ![]() :
:
а) найти величину минимального пути и сам путь от вершины ![]()
![]() до вершины
до вершины ![]() по алгоритму Дейкстры ;
по алгоритму Дейкстры ;
б) используя алгоритм Форда-Фалкерсона, определить максимальный поток ![]() ( v1 – вход , v6 – выход сети ) и указать минимальный разрез, отделяющий v1 от v6 ,
( v1 – вход , v6 – выход сети ) и указать минимальный разрез, отделяющий v1 от v6 ,
если задана матрица весов (длин, пропускных способностей) Р :
v1 v2 v3 v4 v5 v6
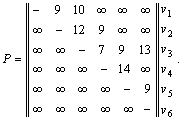
Решение:
Построим сеть:
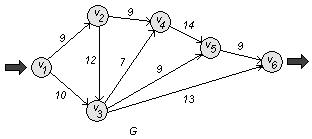
а) Найдем величину минимального пути и сам путь сети G . Используем для этого алгоритм Дейкстры.
Этап 1. Нахождение длины кратчайшего пути.
![]() .
.
Шаг 1. Полагаем ![]()
![]()
1-я итерация.
Шаг 2. Составим множество вершин, непосредственно следующих за ![]() с временными метками:
с временными метками: ![]() . Пересчитываем временные метки этих вершин:
. Пересчитываем временные метки этих вершин: ![]() ,
,
![]() .
.
Шаг 3. Одна из временных меток превращается в постоянную:
![]()
Шаг 4. ![]() Следовательно, возвращаемся на второй шаг.
Следовательно, возвращаемся на второй шаг.
2-я итерация.
Шаг 2.
![]()
![]()
Шаг 3.
![]()
Шаг 4. ![]() Переход на второй шаг.
Переход на второй шаг.
3-я итерация.
Шаг 2.
![]()
![]()
Шаг 3.
![]()
Шаг 4.
![]() Переход на второй шаг.
Переход на второй шаг.
4-я итерация.
Шаг 2.
![]()
Шаг 3.
![]()
Шаг 4. ![]() Переход на второй шаг.
Переход на второй шаг.
5-я итерация.
Шаг 2.
![]()
Шаг 3.
![]()
Шаг 4. ![]() Конец первого этапа.
Конец первого этапа.
Следовательно, длина кратчайшего пути равна ![]() .
.
Этап 2. Построение кратчайшего пути.
1-я итерация.
Шаг 5. Составим множество вершин, непосредственно предшествующих ![]() с постоянными метками :
с постоянными метками : ![]() Проверим равенство
Проверим равенство
![]()
для этих вершин:
![]() т.е.
т.е.
![]()
![]() т.е.
т.е.
![]()
Включаем дугу ![]() в кратчайший путь,
в кратчайший путь, ![]()
Шаг 6. ![]() Возвращаемся на пятый шаг.
Возвращаемся на пятый шаг.
2-я итерация.
Шаг 5.
![]()
![]()
![]()
Включаем дугу ![]() в кратчайший путь,
в кратчайший путь, ![]() .
.
Шаг 6. ![]() . Завершение второго этапа.
. Завершение второго этапа.
Следовательно, кратчайший путь построен. Его образует последовательность дуг: ![]() .
.
Окончательно, кратчайший путь от вершины ![]() до вершины v6 построен. Его длина (вес) равна
до вершины v6 построен. Его длина (вес) равна ![]() . Сам путь образует последовательность дуг:
. Сам путь образует последовательность дуг:
![]()
б) Определим максимальный поток ![]() через сеть G. Для этого используем алгоритм Форда-Фалкерсона.
через сеть G. Для этого используем алгоритм Форда-Фалкерсона.
![]()
Выбираем произвольно путь из вершины v1 в вершину v6 . Пусть это будет путь ![]() . Минимальную пропускную способность на этом пути, равную 10, имеет дуга
. Минимальную пропускную способность на этом пути, равную 10, имеет дуга ![]() , т.е.
, т.е. ![]() Увеличим на этом пути поток до 10 единиц. Дуга
Увеличим на этом пути поток до 10 единиц. Дуга ![]() становится насыщенной. Дуга
становится насыщенной. Дуга ![]() имеет на данный момент пропускную способность, равную 10.
имеет на данный момент пропускную способность, равную 10.
Путь ![]() Следовательно, поток на этом пути можно увеличить на 9 единиц. Дуги
Следовательно, поток на этом пути можно увеличить на 9 единиц. Дуги ![]() становятся насыщенными.
становятся насыщенными.
Других маршрутов нет (другие маршруты проходят через насыщенные дуги). Поток максимален. Делаем разрез вокруг вершины v1 по насыщенным дугам
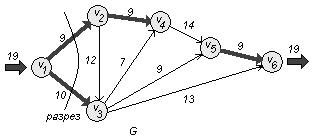
![]()
и получаем его величину ![]() единиц.
единиц.
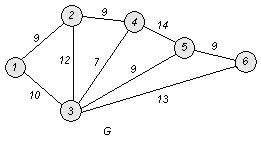
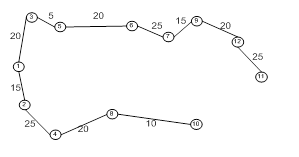
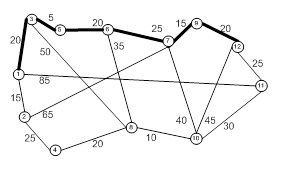
8. Используя алгоритм Краскала, построить остов с наименьшим весом для неориентированного взвешенного графа ![]() , у которого
, у которого ![]() , если заданы веса (длины) ребер:
, если заданы веса (длины) ребер:
![]()
□ Построим граф G :
1. Упорядочим ребра в порядке неубывания веса (длины):
![]()
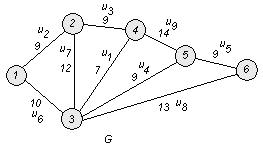
2. Возьмем ребро u1 и поместим его в строящийся остов.
Возьмем ребро u2 и поместим его в строящийся остов (т.к. оно не образует с предыдущим ребром цикла).
Берем ребро u3 и помещаем его в строящийся остов (т.к. оно не образует с предыдущими ребрами цикла).
Берем ребро u4 и помещаем его в строящийся остов (т.к. оно не образует с предыдущими ребрами цикла).
Берем ребро u5 и помещаем его в строящийся остов (т.к. оно не образует цикла с предыдущими ребрами).
Ребра ![]() не рассматриваем, т.к. они образуют циклы с предыдущими ребрами.
не рассматриваем, т.к. они образуют циклы с предыдущими ребрами.
Проверим окончание алгоритма. Число входящих в остов ребер равно 5. Заданный граф имеет п = 6 вершин и ![]() . Таким образом, остов содержит все вершины заданного графа G .
. Таким образом, остов содержит все вершины заданного графа G .
Вес (длина) построенного остова
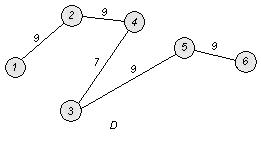
равен ![]()
![]() .
.
Литература
1. Горбатов В.А. Основы дискретной математики. – М.: Высшая школа, 1986. – 311 с.
2. Коршунов Ю.М. Математические основы кибернетики. – М.: Энерго атомиздат, 1987. – 496 с.
3. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988. – 480 с.
4. Шапорев С.Д. Дискретная математика. – СПб.: БХВ-Петербург, 2006. - 400 с.
5. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике. – М.: ФИЗМАТЛИТ, 2005. – 416 с.
6. Хаханов В.И., Чумаченко С.В. Дискретная математика ( конспект теоретического материала). – Харьков: ХНУРЭ, 2003. – 246 с.
7. Богданов А.Е. Курс лекций по дискретной математике.–Северодонецк: СТИ, 2006. – 190 с.
Похожие работы
... подход к разработке эффективного алгоритма для решения любой задачи – изучить ее сущность. Довольно часто задачу можно сформулировать на языке теории множеств, относящейся к фундаментальным разделам математики. В этом случае алгоритм ее решения можно изложить в терминах основных операций над множествами. К таким задачам относятся и задачи информационного поиска, в которых решаются проблемы, ...
... ответ на этот вопрос положителен. Штрих Шеффера является отрицанием конъюнкции, стрелка Пирса – отрицание дизъюнкции, сумма Жегалкина – отрицание эквивалентности. М. Жегалкин (1869–1947) – российский математик и логик, один из основоположников современной математической логики. Чарльз Пирс (1839–1914) – американский логик, математик и естествоиспытатель. Основоположник семиотики, родоначальник ...
элементы теории нечетких множеств можно применять для решения экономических задач в условиях неопределённости. 1. применение Логических функций 1.1 Применение методов дискретной математики в экономике При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом ...
... Задачи, имеющие решение применимое к целому классу подобных задач: это задачи, в формулировке которых не содержится особых деталей, чтобы их решение было применимо к целому классу подобных задач (Пример: задача о метрополитене и т.д.). Задачи. Комнаты музея. Составьте алгоритм-программу определения числа комнат в музее и площади каждой комнаты в клетках. План музея показан ниже на рисунке. ...

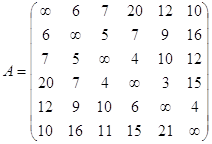
0 комментариев