Навигация
4. Преобразование Лапласа
Преобразование Лапласа — интегральное преобразование, связывающее функцию ![]() комплексного переменного (изображение) с функцией
комплексного переменного (изображение) с функцией ![]() действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.
Интеграл Лапласа имеет вид:
![]() (5)
(5)
где интегрирование производится по некоторому контуру Lв плоскости комплексного переменного z, ставящий в соответствие функции f(z), определенной на L, аналитическую функцию F(p) комплексного переменного p=s+it. Многие интегралы вида (5) были рассмотрены П. Лапласом.
В узком смысле под преобразованием Лапласа подразумевают одностороннее преобразование Лапласа
![]() , (6)
, (6)
называемое так в отличие от двустороннего преобразования Лапласа
![]() (7)
(7)
Преобразование Лапласа – частный вид интегральных преобразований;. преобразования вида (6) или (7) тесно связаны с Фурье преобразованием. Двустороннее преобразование Лапласа (7) можно рассматривать как преобразование Фурье функции ![]() , одностороннее преобразование Лапласа (6) - как преобразование Фурье функции j(t) равной
, одностороннее преобразование Лапласа (6) - как преобразование Фурье функции j(t) равной ![]() при 0 < t < ∞ и равной нулю при -∞ < t < 0.
при 0 < t < ∞ и равной нулю при -∞ < t < 0.
Подынтегральная комплексная локально суммируемая функция f(t) называется функцией-оригиналом, или просто оригиналом; в приложениях часто удобно трактовать переменное t как время. Функция F(p)=L[f], (р) называется также преобразованием Лапласа оригинала f(t) или изображением по Лапласу. Интеграл (6) понимается, вообще говоря, как условно сходящийся на бесконечности.
Априори возможны три случая:
1) существует действительное число ![]() такое, что интеграл (6) сходится при
такое, что интеграл (6) сходится при ![]() , а при
, а при ![]() – расходится; это число σс называется абсциссой (условной) сходимости;
– расходится; это число σс называется абсциссой (условной) сходимости;
2) интеграл (6) сходится при всех р, в этом случае полагают ![]() ;
;
3) интеграл (6) расходится при всех р, в этом случае полагают ![]()
Если ![]() , то интеграл (6) представляет однозначную аналитическую функцию F(p) в полуплоскости сходимости
, то интеграл (6) представляет однозначную аналитическую функцию F(p) в полуплоскости сходимости ![]() . Обычно ограничиваются рассмотрением абсолютно сходящихся интегралов (6). Точная нижняя грань тех s, для которых существует интеграл
. Обычно ограничиваются рассмотрением абсолютно сходящихся интегралов (6). Точная нижняя грань тех s, для которых существует интеграл ![]() , называется абсциссой абсолютной сходимости
, называется абсциссой абсолютной сходимости ![]()
![]()
Если а – есть нижняя грань тех s, для которых ![]() число а иногда называют показателем роста оригинала f(t).
число а иногда называют показателем роста оригинала f(t).
При некоторых дополнительных условиях оригинал f(t) однозначно восстанавливается по своему F(p). Например, если f(t) имеет ограниченную вариацию в окрестности точки t0 или если f(t) кусочногладкая, то имеет место формула обращения преобразования Лапласа:
![]() (8)
(8)
Формулы (6) и (8) позволяют получить ряд соотношений между операциями, производимыми над оригиналами и изображениями, а также таблицу изображений для часто встречающихся оригиналов. Все это составляет элементарную часть операционного исчисления.
В математической физике важные применения находит многомерное преобразование Лапласа:
![]() (9)
(9)
где t = (t1, ……, tn)
-точка re-мерного евклидова пространства
Rn, p = (p1, ……, pn) = σ + iτ = (σ1, ……, σn) + (τ1, ……, τn)
-точка комплексного пространства
Cn, n≥1, (p,t) = (σ,t)+i(τ,t) = p1t1 + … +pntn
-скалярное произведение, dt = dt1…dtn - элемент объема в Rn. Комплексная функция f(t) в (9) определена и локально суммируема в области интегрирования
![]()
-положительном координатном угле пространства Rn. Если функция f(t) ограничена в C*, то интеграл (9) существует во всех точках ![]() удовлетворяющих условию Re(p,t)>0,
удовлетворяющих условию Re(p,t)>0, ![]() , которое определяет снова положительный координатный угол
, которое определяет снова положительный координатный угол
![]()
Интеграл (9) определяет голоморфную функцию комплексных переменных p = (p1 ,- pn) в трубчатой области![]() пространства
пространства ![]() с основанием S. В более общем случае в качестве области интегрирования
с основанием S. В более общем случае в качестве области интегрирования![]() в (9) и основания Sтрубчатой области можно взять любую пару сопряженных замкнутых выпуклых острых конусов в пространстве
в (9) и основания Sтрубчатой области можно взять любую пару сопряженных замкнутых выпуклых острых конусов в пространстве ![]() с вершиной в начале координат. При n=1 формула (9) переходит в (6), причем
с вершиной в начале координат. При n=1 формула (9) переходит в (6), причем ![]() - положительная полуось и
- положительная полуось и ![]() - правая полуплоскость. Преобразование Лапласа (9) определено и голоморфно и для функций f(t) гораздо более широких классов. Элементарные свойства преобразования Лапласа с соответствующими изменениями остаются справедливыми и для многомерного случая.
- правая полуплоскость. Преобразование Лапласа (9) определено и голоморфно и для функций f(t) гораздо более широких классов. Элементарные свойства преобразования Лапласа с соответствующими изменениями остаются справедливыми и для многомерного случая.
Численное преобразование Лапласа - численное выполнение преобразования (6), переводящего оригинал f(t), 0<t<∞ в изображение F(p),![]() , а также численное обращение преобразования Лапласа, т. е. численное нахождение f(t) из интегрального уравнения (6) либо по формуле обращения (8).
, а также численное обращение преобразования Лапласа, т. е. численное нахождение f(t) из интегрального уравнения (6) либо по формуле обращения (8).
Необходимость применения численного преобразования Лапласа возникает вследствие того, что таблицы оригиналов и изображений охватывают далеко не все встречающиеся в практике случаи, а также вследствие того, что оригинал или изображение зачастую выражаются слишком сложными, неудобными для применений формулами.
Проблема обращения преобразования Лапласа, как задача отыскания решения f(x) интегрального уравнения первого рода (6), относится к классу некорректных задач и может быть решена, в частности, посредством регуляризирующего алгоритма.
Задачу численного обращения преобразования Лапласа можно также решать методами, основанными на разложении функции-оригинала в функциональный ряд. Сюда в первую очередь можно отнести разложение в степенной ряд, в обобщенный степенной ряд, в ряд по показательным функциям, а также в ряды по ортогональным функциям, в частности по многочленам Чебышева, Лежандра, Якоби и Лагерра. Задача разложения оригинала в ряды по многочленам Чебышева, Лежандра, Якоби в окончательном своем виде сводится к проблеме моментов на конечном промежутке. Пусть известно преобразование Лапласа F(p) функции β(t)f(t):
![]()
где f(t) - искомая функция, а β(t) - неотрицательная, интегрируемая на [0,∞) функция. Предполагается, что функция f(t) интегрируема на любом конечном отрезке [0, Т] и принадлежит классу L2(β(t), 0, ∞).По изображению F(р).функции β(t), f(t), функция f(t) строится в виде ряда по смещенным многочленам Якоби, в частности по смещенным многочленам Лежандра, Чебышева первого и второго рода, коэффициенты которого ak вычисляются по формуле.
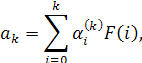
где ![]() - коэффициенты смещенного многочлена Лежандра, Чебышева первого и второго рода соответственно, записанных в виде
- коэффициенты смещенного многочлена Лежандра, Чебышева первого и второго рода соответственно, записанных в виде ![]()
Другим приемом численного обращения преобразования Лапласа является построение квадратурных формул для интеграла обращения (8).
Похожие работы
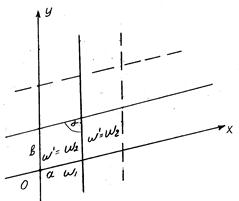
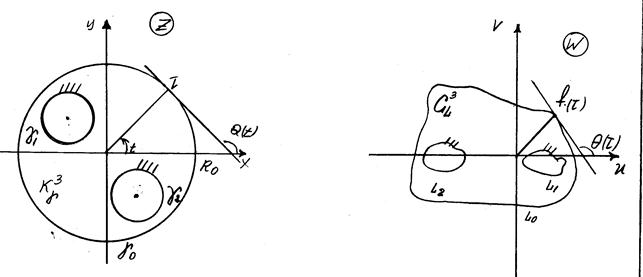
... (72) и (73) положить , то мы получим две интегральные формулы Пуассона для кругового кольца: , (82) , (83) где (74) и (75) – реальные и мнимые части компактной интегральной формулы Вилля-Шварца для кругового кольца [2], - функция Вейерштрасса, - угол наклона касательной к в точке , , - периоды, с – произвольная постоянная, (). Так как функция ) представляется быстро сходящимися ...
0 комментариев