Навигация
Обращение преобразования Лапласа с помощью многочленов, ортогональных на конечном промежутке
4. Обращение преобразования Лапласа с помощью многочленов, ортогональных на конечном промежутке
4.1 Постановка задачи
Задачу преобразования Лапласа можно решать методами, основанными на разложении оригинала в ряды по ортогональным функциям, в частности по многочленам Чебышева, Лежандра и Якоби.Эта задача, которая в окончательном своем виде сводится к проблеме моментов на конечном промежутке, была подвергнута изучению в работах многих авторов.
Рассмотрим постановку этой задачи в таком виде, как это сделано в работах В.М. Амербаева и в книге В.А. Диткина и А.П. Прудникова [2].
Пусть известно преобразование Лапласа F(p) функции β(t)f(t):
![]() (10)
(10)
Где f(t) – искомая функция, а β(t) – неотрицательная, абсолютно интегрируемая на [0,∞) функция. Предположим, что функция f(t) интегрируема на любом конечном отрезке [0, Т] и принадлежит классу L2(β(t), 0, ∞):
![]() (11)
(11)
Требуется по изображению F(р) функции β(t)f(t), построить функцию f(t).
В интеграле (10) введем замену переменной x=e-t; тогда он приведется к виду
![]() (12)
(12)
где
![]()
В силу условий, которые наложены на функции f(t) и β(t), интеграл (12) сходится всюду в плоскости Re p≥,0, поэтому переменной р можно придать значения 0, 1, 2, … и получить «взвешенные моменты» функции ![]()
![]() (13)
(13)
После этого решаемую задачу можно сформулировать так: найти функцию ![]() по ее «взвешенным моментам»
по ее «взвешенным моментам» ![]() , или, что тоже самое, найти функцию f(t) по значениям изображения функции β(t)f(t) в целочисленных точках p = k (k = 0, 1, 2, …). В частном случае эту задачу можно упростить и по первым п + 1 «взвешенным моментам» искать многочлен
, или, что тоже самое, найти функцию f(t) по значениям изображения функции β(t)f(t) в целочисленных точках p = k (k = 0, 1, 2, …). В частном случае эту задачу можно упростить и по первым п + 1 «взвешенным моментам» искать многочлен ![]() , такой, чтобы его «взвешенные моменты» совпадали с заданными моментами функции
, такой, чтобы его «взвешенные моменты» совпадали с заданными моментами функции ![]() , то есть чтобы выполнялись равенства
, то есть чтобы выполнялись равенства
![]() (14)
(14)
4.2.Обращение преобразования Лапласа с помощью смещенных многочленов Лежандра
Рассмотрим частный случай весовой функции
![]() (15)
(15)
![]() или
или ![]() .
.![]()
Многочленами, ортогональными на отрезке [0,1] с весом ![]() , будут смещены многочлены Лежандра
, будут смещены многочлены Лежандра ![]()
Они задаются формулой
![]() при
при ![]()
или же формулой
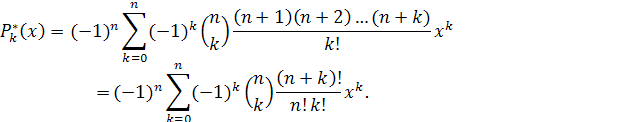
Величина rn в этом случае равна
![]()
и разложение функции f(t) по смещенным многочленам Лежандра имеет вид
![]() (16)
(16)
Величины αk вычисляются по формуле
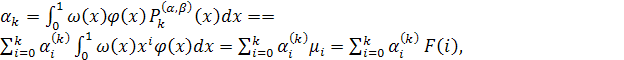 (17)
(17)
в которой ![]() - коэффициенты смещенного многочлена Лежандра
- коэффициенты смещенного многочлена Лежандра ![]()
4.3. Обращение преобразования Лапласа с помощью смещенных многочленов Чебышева первого рода.
Положим теперь ![]() Весовая функция имеет вид
Весовая функция имеет вид
![]() и
и ![]()
Смещенные многочлены Чебышева первого рода ![]() являются ортогональной системой на [0,1] по весу
являются ортогональной системой на [0,1] по весу ![]()
Многочлены Якоби ![]() отличаются от
отличаются от ![]() только численным множителем, а именно
только численным множителем, а именно
![]() ,
,
где![]()
Многочлены ![]() имеют вид
имеют вид
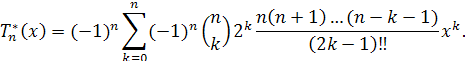
Значения rn вычисляются по формулам
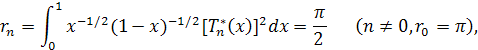
а разложение функции f(t) по смещенным многочленам Чебышева первого рода имеет вид
![]() (18)
(18)
Коэффициенты ak (k=0, 1, …) вычисляются по формуле (17), в которой ![]() - коэффициенты смещенного многочлена Чебышева первого рода
- коэффициенты смещенного многочлена Чебышева первого рода ![]() .
.
В вычислениях удобнее пользоваться тригонометрической записью многочленов ![]() , а именно:
, а именно:![]()
Сделав замену переменной 2x – 1 = cosθ (0≤θ≤π)
и учитывая, что ![]() разложение (18) можно переписать в виде:
разложение (18) можно переписать в виде:
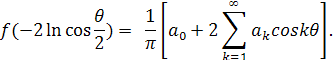
ЗАКЛЮЧЕНИЕ
Одним из наиболее мощных средств решения дифференциальных уравнений, как обыкновенных, так, особенно, в частных производных, является метод интегральных преобразований.
Преобразования Фурье, Лапласа, Ганкеля и другие применяются для решения задач теории упругости, теплопроводности, электродинамики и других разделов математической физики.
Преобразование Лапласа — интегральное преобразование, связывающее функцию ![]() комплексного переменного (изображение) с функцией
комплексного переменного (изображение) с функцией ![]() действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями.
Интеграл Лапласа имеет вид:
![]()
где интегрирование производится по некоторому контуру Lв плоскости комплексного переменного z, ставящий в соответствие функции f(z), определенной на L, аналитическую функцию F(p) комплексного переменного p=s+it.
Численное преобразование Лапласа - численное выполнение преобразования
![]() ,
,
переводящего оригинал f(t), 0<t<∞ в изображение F(p),![]() , а также численное обращение преобразования Лапласа.
, а также численное обращение преобразования Лапласа.
Необходимость применения численного преобразования Лапласа возникает вследствие того, что таблицы оригиналов и изображений охватывают далеко не все встречающиеся в практике случаи, а также вследствие того, что оригинал или изображение зачастую выражаются слишком сложными, неудобными для применений формулами.
Задачу численного обращения преобразования Лапласа можно также решать методами, основанными на разложении функции-оригинала в функциональный ряд. Сюда в первую очередь можно отнести разложение в степенной ряд, в обобщенный степенной ряд, в ряд по показательным функциям, а также в ряды по ортогональным функциям, в частности по многочленам Чебышева, Лежандра, Якоби и Лагерра. Задача разложения оригинала в ряды по многочленам Чебышева, Лежандра, Якоби в окончательном своем виде сводится к проблеме моментов на конечном промежутке. Пусть известно преобразование Лапласа F(p) функции β(t)f(t):
![]()
где f(t) - искомая функция, а β(t) - неотрицательная, интегрируемая на [0,∞) функция.
СПИСОК ЛИТЕРАТУРЫ
1. Ван дер Поль Б., Бремер Х. Операционное исчисление на основе двустороннего преобразования Лапласа. — М.: Издательство иностранной литературы, 1952. — 507 с.
2. Диткин В.А., Прудников А. П. Интегральные преобразования и операционное исчисление. — М.: Главная редакция физико-математической литературы издательства «Наука», 1974. — 544 с.
3. Кожевников Н.И., Краснощекова Т. И., Шишкин Н. Е. Ряды и интегралы Фурье. Теория поля. Аналитические и специальные функции. Преобразования Лапласа. — М.: Наука, 1964. — 184 с.
4. Крылов В.И., Скобля Н.С. Методы приближенного преобразования Фурье и обращения преобразования Лапласа. – М.: Наука, 1974. – 226 с.
Похожие работы
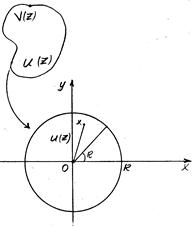
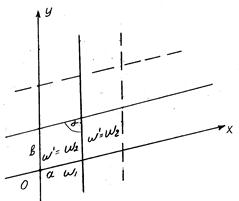
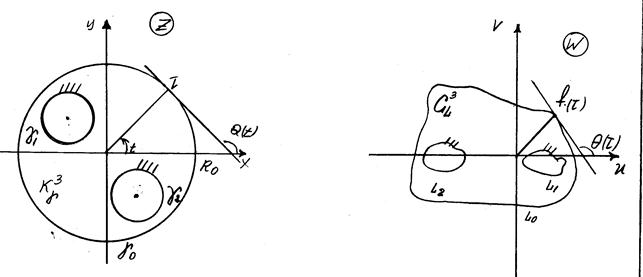
... (72) и (73) положить , то мы получим две интегральные формулы Пуассона для кругового кольца: , (82) , (83) где (74) и (75) – реальные и мнимые части компактной интегральной формулы Вилля-Шварца для кругового кольца [2], - функция Вейерштрасса, - угол наклона касательной к в точке , , - периоды, с – произвольная постоянная, (). Так как функция ) представляется быстро сходящимися ...
0 комментариев